Binääridekooderi on digitaalinen piiri, joka muuntaa binäärikoodin joukoksi lähtöjä. Binäärikoodi edustaa halutun lähdön sijaintia ja sitä käytetään valitsemaan tietty aktiivinen lähtö. Binääridekooderit ovat enkooderien käänteisiä, ja niitä käytetään yleisesti digitaalisissa järjestelmissä sarjakoodin muuntamiseen rinnakkaisten lähtöjen joukoksi.

1. Binääridekooderin perusperiaate on määrittää yksilöllinen lähtö jokaiselle mahdolliselle binäärikoodille. Esimerkiksi binääridekooderi, jossa on 4 tuloa ja 2^4 = 16 ulostuloa, voi määrittää yksilöllisen lähdön jokaiselle 16 mahdolliselle 4-bittiselle binäärikoodille.
2. Binääridekooderin tulot ovat yleensä aktiivisia alhaalla, mikä tarkoittaa, että vain yksi tulo on aktiivinen (matala) kerrallaan ja muut tulot ovat passiivisia (high). Aktiivista matalaa tuloa käytetään valitsemaan tietty aktiivinen lähtö.
3. On olemassa erityyppisiä binääridekoodereita, mukaan lukien prioriteettidekooderit, jotka määrittävät prioriteetin jokaiselle lähdölle, ja virheen havaitsevat dekooderit, jotka voivat havaita virheet binäärikoodissa ja tuottaa virhesignaalin.

Yhteenvetona voidaan todeta, että binääridekooderi on digitaalinen piiri, joka muuntaa binäärikoodin joukoksi lähtöjä. Binääridekooderit ovat kooderien käänteisiä osia, ja niitä käytetään laajalti digitaalisissa järjestelmissä sarjakoodien muuntamiseen rinnakkaislähtöisiksi.

Digitaalisessa elektroniikassa erillisiä informaatiomääriä edustavat binäärikoodit. Binäärikoodi n bittiä pystyy edustamaan jopa 2^n erillistä elementtiä koodatusta tiedosta. Nimi Dekooderi tarkoittaa koodatun tiedon kääntämistä tai dekoodaamista yhdestä formaatista toiseen, joten digitaalinen dekooderi muuntaa joukon digitaalisia tulosignaaleja vastaavaksi desimaalikoodiksi lähdöessään. A dekooderi on yhdistelmäpiiri joka muuntaa binääritiedot n syöttöriviä maksimissaan 2^n ainutlaatuista lähtölinjaa .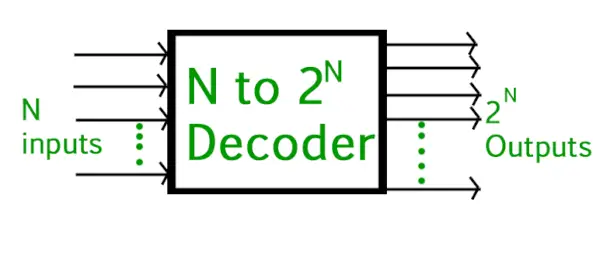

Binääridekooderi -

• Binääridekooderit ovat toisen tyyppisiä digitaalisia logiikkalaitteita, joissa on 2-, 3- tai 4-bittisten koodien tulot riippuen datan syöttölinjojen määrästä, joten dekooderi, jossa on kahden tai useamman bitin sarja, määritellään seuraavasti: jolla on n-bittinen koodi, ja siksi on mahdollista esittää 2^n mahdollista arvoa.
• Jos binääridekooderi vastaanottaa n sisääntuloa, se aktivoi yhden ja vain yhden 2^n lähdöstään tämän tulon perusteella kaikkien muiden lähdöiden ollessa deaktivoituina. Jos n-bittisellä koodatulla tiedolla on käyttämättömiä yhdistelmiä, dekooderilla voi olla vähemmän kuin 2^n lähtöä.
• Esimerkki: invertteri (NOT-gate) voidaan luokitella 1-2-binääridekooderiksi, koska 1-tulo ja 2-lähtö on mahdollista. eli tulo A voi antaa joko A- tai A-komplementin ulostulona.
• Sitten voidaan sanoa, että standardi yhdistelmälogiikkadekooderi on n-m-dekooderi, jossa m <= 2^n ja jonka lähtö, Q on riippuvainen vain sen nykyisistä tulotiloista.
• Niiden tarkoitus on tuottaa 2^n (tai vähemmän) mintermiä n syötemuuttujasta. Jokainen tulojen yhdistelmä tuottaa ainutlaatuisen lähdön.

Binääridekooderi muuntaa koodatut tulot koodatuiksi ulostuloiksi, joissa tulo- ja lähtökoodit ovat erilaiset ja dekoodeja on saatavana joko binaari- tai BCD- (8421-koodi) -sisääntulokuvion dekoodaamiseksi tyypillisesti desimaalilähtökoodiksi. Käytännön binääridekooderipiirejä ovat 2-4-, 3-8- ja 4-16-linjaiset konfiguraatiot.

2-4-binääridekooderi –

Yllä kuvattu 2-4-rivinen binääridekooderi koostuu neljän JA-portin joukosta. Kaksi binaarituloa, jotka on merkitty A ja B, dekoodataan yhdeksi neljästä lähdöstä, tästä syystä 2-4-binääridekooderin kuvaus. Jokainen tulos edustaa yhtä kahden tulomuuttujan mintermistä (jokainen tulos = minterm). Lähtöarvot ovat: Qo=A'B' Q1=A'B Q2=AB' Q3=AB Binääritulot A ja B määrittävät, mikä lähtölinja Q0:sta Q3:een on KORKEA logiikkatasolla 1, samalla kun muut lähdöt pidetään yllä. LOW logiikalla 0, joten vain yksi lähtö voi olla aktiivinen (HIGH) kerrallaan. Siksi se, kumpi lähtörivi on KORKEA, tunnistaa sisääntulossa olevan binäärikoodin, toisin sanoen se dekoodaa binääritulon. Joissakin binääridekoodereissa on ylimääräinen sisääntulonasta nimeltä Enable, joka ohjaa laitteen lähtöjä. Tämän lisätulon avulla dekooderin lähdöt voidaan kytkeä päälle tai pois päältä tarpeen mukaan. Lähtö luodaan vain, kun Ota käyttöön -tulon arvo on 1; Muuten kaikki lähdöt ovat 0. Toteutuksessa tarvitaan vain pieni muutos: Enable-syöte syötetään AND-portteihin, jotka tuottavat lähdöt. Jos Enable on 0, kaikki JA-portit syötetään yhdellä tuloista 0:na, joten lähtöä ei synny. Kun Enable on 1, AND-portit saavat yhden tuloista arvona 1, ja nyt lähtö riippuu jäljellä olevista tuloista. Siten dekooderin lähtö riippuu siitä, onko Enable korkea vai matala. GATE CS Corner kysymyksiä Seuraavien kysymysten harjoitteleminen auttaa sinua testaamaan tietosi. Kaikki kysymykset on esitetty GATEssa aiempina vuosina tai GATE Mock Tests -testeissä. On erittäin suositeltavaa harjoitella niitä.

1. GATE CS 2007, kysymys 85
2. GATE CS 20130, kysymys 65

Binääridekooderien käytön edut digitaalisessa logiikassa:

1. Lisääntynyt joustavuus: Binääridekooderit tarjoavat joustavan tavan valita yksi useista lähdöistä binäärikoodin perusteella, mikä mahdollistaa laajan valikoiman sovelluksia.
2. Parempi suorituskyky: Muuntamalla sarjakoodin rinnakkaislähtöjen joukoksi binääridekooderit voivat parantaa digitaalisen järjestelmän suorituskykyä vähentämällä aikaa, joka tarvitaan tiedon siirtämiseen yhdestä tulosta useisiin lähtöihin.
3. Parempi luotettavuus: Binääridekooderit voivat vähentää tiedonsiirrossa tapahtuvien virheiden mahdollisuutta vähentämällä niiden juovien määrää, jotka tarvitaan tiedon siirtämiseen yhdestä tulosta useisiin lähtöihin.

Binääridekooderien käytön haitat digitaalisessa logiikassa:

1. Lisääntynyt monimutkaisuus: Binaaridekooderit ovat tyypillisesti monimutkaisempia piirejä kuin demultiplekserit, ja ne vaativat lisäkomponentteja toteuttaakseen.
2. Rajoitettu tiettyihin sovelluksiin: Binääridekooderit soveltuvat vain sovelluksiin, joissa sarjakoodi on muunnettava rinnakkaislähtöjen joukoksi.
3. Rajoitettu määrä lähtöjä: Binääridekooderien lähtömäärä on rajoitettu, koska lähtöjen lukumäärä määräytyy sisääntulojen ja käytetyn binäärikoodin mukaan.

Yhteenvetona voidaan todeta, että binääridekooderit ovat hyödyllisiä digitaalisia piirejä, joilla on etunsa ja haittansa. Valinta siitä, käytetäänkö binaarista dekooderia vai ei, riippuu järjestelmän erityisvaatimuksista ja monimutkaisuuden, luotettavuuden, suorituskyvyn ja kustannusten välisistä kompromisseista.

Binaaridekooderin käyttö digitaalisessa logiikassa:

1. Muisti pyrkii: Tietokoneistetuissa kehyksissä parillisia dekoodeja käytetään yleensä valitsemaan tietty muistialue useista muistialueista. Sijaintitulot syötetään kaksoisdekooderille, ja vertailumuistialue valitaan.

Oracle sql ei ole sama

2. Ohjauspiirit: Rinnakkaisdekoodeja käytetään latauspiireissä ohjaussignaalien tuottamiseen eri tehtäviin. Esimerkiksi mikrosirussa käytetään kaksoisdekooderia kääntämään ohjaustoimintokoodi ja tuottamaan ohjaussignaaleja vertailua varten.

3. Näytön ajurit: I n tietokoneistettuja kehyksiä, joiden käyttö näyttää gadgeteja, esimerkiksi Drove-esityksiä, rinnakkaisia ​​dekoodeja käytetään esityksen ohjaamiseen. Kaksinkertaiset tietolähteet käytetään dekooderissa, ja niihin liittyvä Drove valaistuu.

4. Osoitteen purkaminen: Rinnakkaisdekoodeja käytetään osoitteen erotuspiireissä luomaan sirun valintamerkki tietylle muistille tai reunalle gadget.

kuinka suuri näyttöni on

5.Digitaalinen kirjeenvaihto: Kehittyneissä kirjeenvaihtojärjestelmissä käytetään kaksinkertaisia ​​dekoodeja kirjeenvaihtokanavan kautta saadun tietokoneistetun tiedon purkamiseen.

6. Virheen korjaus: Kaksoisdekoodeja käytetään virheenkorjauspiireissä tunnistamaan ja korjaamaan tietokoneistetun tiedon virheitä.

Referenssit -

Tässä on muutamia kirjoja, joihin voit tutustua saadaksesi lisätietoja digitaalisesta logiikasta ja binääridekoodereista:

1. Charles H. Roth Jr. ja Lizy Kurian John digitaalisten järjestelmien suunnittelu VHDL:ää käyttäen
2. David Harrisin ja Sarah Harrisin digitaalinen suunnittelu ja tietokonearkkitehtuuri
3. Digitaalisen suunnittelun periaatteet Daniel D. Gajski, Frank Vahid ja Tony Givargis
4. Digitaalinen piirisuunnittelu: Thomas L. Floydin ja David Money Harrisin esittely
5. Thomas L. Floydin Digital Fundamentals

Nämä kirjat kattavat erilaisia ​​digitaalisen logiikan ja suunnittelun aiheita, mukaan lukien binääridekooderit, ja tarjoavat syvällistä tietoa digitaalisten piirien teoriasta, suunnittelusta ja toteutuksesta.

electronicshub – binaarinen dekooderi