Kortin todennäköisyys on pelikorttipakan tapahtumien todennäköisyys. Kuten tiedämme, todennäköisyys on yksi tärkeimmistä matematiikan aiheista, joka käsittelee minkä tahansa tapahtuman mahdollisuuden laskemista. Yksinkertaisesti sanottuna kortin todennäköisyys on osa todennäköisyyttä, jossa löydämme todennäköisyyden nostaa kortti korttipakasta. Tässä artikkelissa opimme korttien todennäköisyydestä ja kaikki yksityiskohdat korttien todennäköisyyskaaviosta, pelikorttien todennäköisyydestä, kortin todennäköisyyden löytämisestä ja ratkaistuja esimerkkejä korttien todennäköisyydestä. Aloitetaan oppiminen aiheesta kortin todennäköisyys.
Mikä on todennäköisyys?
Todennäköisyys on matematiikan haara, joka tutkii mahdollisuuksia tapahtuako jokin tapahtuma vai ei. Matemaattisesti se ei ole muuta kuin suotuisten tulosten lukumäärän suhde tapahtuman tulosten kokonaismäärään (näytteen tila).
Jotkut tosielämän esimerkkejä todennäköisyydestä ovat:
- Korttipelien pelaaminen pelin voittamisen tai häviämisen todennäköisyyden selvittämiseksi.
- Sään ennustaminen, sateen ennustamiseen.
- Vaalitulokset sen määrittämiseksi, voittaako vai häviääkö ehdokas.
- Tenttitulokset, joiden avulla selvitetään, läpäiseekö kokeen vai ei.
Todennäköisyyskaava
Jos E on tapahtuma, jonka näyteavaruus on S ja suotuisten tulosten lukumäärä on n(E), tapahtuman E todennäköisyys eli P(E) saadaan kaavalla:
P(E) = n(E) / n(S)
Mikä on kortin todennäköisyys?
Todennäköisyyttä nostaa kortti tai kerätä korttipakasta kutsutaan kortin todennäköisyydeksi. Yksinkertaisesti sanottuna pelikortteihin liittyvää todennäköisyyttä kutsutaan kortin todennäköisyydeksi. Koska tämä on todennäköisyystyyppi, se on aina välillä 0 ja 1. Esimerkiksi, jos meidän on löydettävä todennäköisyys nostaa ässä korttipakasta, eli 4/52 = 1/13 [Koska ässää on 4 52 kortin pakassa].
Todennäköisesti korttipakka
Deck of Cards on 52 kortin kokoelma, jotka näyttävät olleen olemassa tuhansia vuosia. Korttipakan tai pelikorttien katsotaan olevan peräisin joko Intiasta tai Kiinasta, ensimmäinen dokumentoitu todiste näistä korteista löytyy 9.th-luvun Kiinassa Tang-dynastian aikana. Nämä kortit olivat samankaltaisia kuin nykyajan kortit ja jaettiin myös neljään makuun, mutta niiden nimet ja symbolit ovat erilaisia, eli kolikot, kolikkosarjat, myriadit ja myriadit kymmeniä.
Nykyään näitä kortteja on eri malleissa ja ne on jaettu neljään makuun, nimittäin Spade (♠), Club (♣), Heart (❤) ja Diamond (◆). Yhdelle valitulle kortille näytetila, jos 52, eli yhden valitun kortin tulosten kokonaismäärä pakasta on 52.
n(S) korttipakassa = 52
Korttityypit pakassa
Kaikki korttipakat voidaan luokitella monella tapaa, joitain parametreja, joiden perusteella kortit voidaan luokitella, ovat:
- Perustuu väreihin
- Perustuu Suits
Ymmärretään tämä luokittelu yksityiskohtaisesti seuraavasti:
Perustuu väreihin
Värien perusteella korttipakka voidaan luokitella kahteen luokkaan,
- Punaiset kortit
- Mustat kortit
Yhteensä 52 korttia on jaettu tasan punaisiin ja mustiin, mikä tarkoittaa, että pakassa on 26 punaista ja 26 mustaa korttia.
Perustuu Suits
Korttipakassa on neljä maata, jotka ovat:
- Sydämet (❤)
- Timantit (◆)
- Klubit (♣)
- Pata (♠)
Näiden lisäksi on olemassa vielä yksi korttiluokitus, joka perustuu korttien järjestykseen:
- Ässä
- Numerokortit
- Kasvokortit
Ässä
Ässä on yksi tällainen kortti, joka on joko tärkein tai vähiten tärkeä pelin perusteella. Tämä kortti A on kirjoitettu siihen ja jokaisessa maassa on yksi tällainen kortti eli neljä ässäkorttia.
Numerokortit
2-10 korttia on 9 per maata, joten tällaisia kortteja on yhteensä 36.
Kasvokortit
Kasvokortit, kuten nimestä voi päätellä, sisältävät hahmon tai hahmon kasvot kortissa. Jokaisesta maasta on kolme korttia eli Jack, Queen, King. Kasvokortteja on siis yhteensä 12.
Kaikki nämä luokitukset näkyvät seuraavassa taulukossa.
| Korttipakka (52 korttia) | ||||
|---|---|---|---|---|
| Värilliset kortit | Mustat kortit (26 korttia) | Punaiset kortit (26 korttia) | ||
| Puvut | Spade (13 korttia) | Club (13 korttia) | Sydän (13 korttia) | Timantti (13 korttia) |
| Kasvokortit (12 korttia pakassa ja 3 korttia jokaisessa maassa) | K (kuningas) | K (kuningas) | K (kuningas) | K (kuningas) |
| Q (kuningatar) | Q (kuningatar) | Q (kuningatar) | Q (kuningatar) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Numerokortit (36 korttia pakassa ja 9 korttia maassa) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Ässä-kortit (4 korttia pakassa ja 1 kortti maassa) | A (ässä) | A (ässä) | A (ässä) | A (ässä) |
Korttipakan kaavio
Seuraava taulukko esittää pelikorttipakan luokituksen:
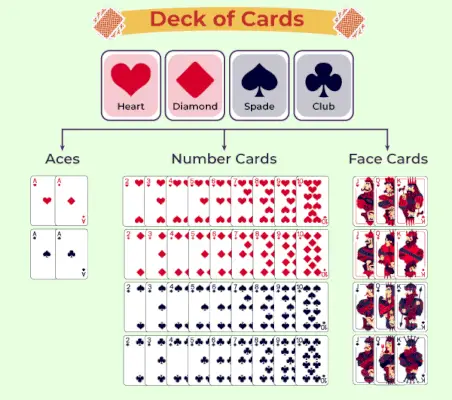
Pelikortin todennäköisyys
Joitakin yleisiä korttien todennäköisyyksien tapahtumia käsitellään seuraavassa taulukossa:
| Tapahtuma E kortin piirtämiseen | Todennäköisyys P(E) |
|---|---|
| Ässä | P(E) = 4/52 = 1/13 |
| Kuningas | P(E) = 4/52 = 1/13 |
| Numerokortti | P(E) = 36/52 = 9/13 |
| Kasvokortti | P(E) = 12/52 = 3/13 |
| Spade kortti | P(E) = 13/52 = 1/4 |
| Punainen kortti | P(E) = 26/52 = 1/2 |
Kuinka löytää korttien todennäköisyys?
Vaiheet kortteja sisältävien tapahtumien todennäköisyyden selvittämiseksi ovat samat kuin kaikki muutkin todennäköisyydet, jotka on annettu seuraavasti:
Vaihe 1: Selvitä ensin annetusta kysymyksestä saatujen myönteisten tulosten lukumäärä.
Vaihe 2: Etsi sitten tulosten kokonaismäärä.
Vaihe 3: Käytä todennäköisyyskaavaa löytääksesi kortin todennäköisyys.
Esimerkki: Mikä on todennäköisyys nostaa ässä korttipakasta?
Vastaus:
Tässä E on ässä-kortin nostaminen
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = ässäkortin nostaminen pakasta = 4 (Yhdessä pakassa on 4 ässäkorttia)
P(E) = n(E) / n(S) = 4/52
P(E) = 1/13
Todennäköisyys nostaa ässäkortti = 1/13
Esimerkkikysymyksiä kortin todennäköisyydestä
Tehtävä 1: Millä todennäköisyydellä nostetaan seuraavat kortit korttipakasta?
(i) lapio
(ii) musta kortti
(iii) numerokortti
Ratkaisu:
(i) Tässä E on lapiokortin nostaminen
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = lapiokortin nosto pakasta = 13 (Yhdessä pakassa on 13 korttia jokaisesta maasta)
P(E) = n(E) / n(S) = 13/52
P(E) = 1/4
Lapion piirtämisen todennäköisyys = 1/4
(ii) Tässä E on mustan kortin nostaminen
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = mustan kortin nostaminen pakasta = 26 (yhdessä pakassa on 26 mustaa korttia)
P(E) = n(E) / n(S) = 26/52
P(E) = 1/2
Todennäköisyys nostaa musta kortti = 1/2
(iii) Tässä E on numerokortin nostaminen
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = numerokortin nostaminen pakasta = 36 (Yhdessä pakassa on 36 numerokorttia)
P(E) = n(E) / n(S) = 36/52
P(E) = 9/13
Numerokortin piirtämisen todennäköisyys = 9/13
Tehtävä 2: Millä todennäköisyydellä nostetaan seuraavat kortit korttipakasta?
(i) Kuningas tai musta kortti
(ii) Punainen ja ässäkortti
Ratkaisu:
(i) Tässä E tarkoittaa kuninkaan tai mustan kortin nostamista
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = kuninkaan tai mustan kortin nostaminen pakkasta = 26 + 2 = 28 (On 26 mustaa korttia, joista 2 on kuningas ja jäljellä 2 mustaa kuningasta 1 pakassa)
P(E) = n(E) / n(S) = 28/52
P(E) = 7/13
Todennäköisyys nostaa kuningas tai musta kortti = 7/13
(ii) Tässä E on tapahtuma, jossa nostetaan punainen ja ässä kortti
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = punaisen ja ässäkortin nostaminen pakasta = 2 (Punaista korttia on 26, joista 2 on ässäkorttia)
Kysymyksen mukaan vedetyn kortin tulee olla punainen ja molemmat ässä. Siksi n(E) = 2
P(E) = n(E) / n(S) = 2/52
P(E) = 1/26
Todennäköisyys nostaa punainen ja ässä kortti = 1/26
Tehtävä 3: Millä todennäköisyydellä nostetaan seuraavat kortit korttipakasta?
(i) Ei-klubikortti
(ii) Ei-kasvokortti
saada taulukon pituus c
Ratkaisu:
(i) Tässä E on ei-klubikortin nostaminen
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = ei-seurakortin nostaminen pakasta = 39 (Yhdessä pakassa on 13 mailaa, ei-pakassa = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39/52
P(E) = 3/4
Todennäköisyys nostaa ei-klubikortti = 3/4
(ii) Tässä E on ei-face-kortin nostaminen
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = ei-kasvokortin nostaminen pakkasta = 40 (yhdessä pakassa on 12 kasvokorttia, ei-pakassa = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40/52
P(E) = 10/13
Todennäköisyys nostaa ei-klubikortti = 10/13
Tehtävä 4: Mikä on todennäköisyys nostaa kortti, joka ei ole punainen eikä kuvakortti?
Ratkaisu:
Tässä E on tapahtuma, jossa ei nosta punaista eikä kasvokorttia
Pakan tulosten kokonaismäärä n(S) = 52
Myönteisten tulosten lukumäärä = n(E) = ei punaista eikä kasvokorttia nostettu pakkasta.
Punaisia kortteja yhteensä = 26
Pakassa on yhteensä 12 kasvokorttia, mutta 6 punaista korttia on jo poistettu. Joten jäljellä olevat kuvakortit = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/52
P(E) = 8/13
Todennäköisyys nostaa ei punaista eikä kasvokorttia = 8/13
Tehtävä 5: Millä todennäköisyydellä korttipakasta nostetaan kaksi korttia korvaamalla, kun ensimmäinen kortti on sydän ja toinen timantti?
Ratkaisu:
Todennäköisyys nostaa ensimmäinen kortti sydämeksi = 13/52
Ensimmäisen kortin nostamisen jälkeen kortti poistetaan.
Todennäköisyys vetää toinen kortti timantiksi = 13/51
Todennäköisyys nostaa ensimmäinen kortti sydämeksi ja toinen timantiksi = (13 / 52) × (13 / 51)
Todennäköisyys vetää ensimmäinen kortti sydämeksi ja toinen timantiksi = 13/204
Usein kysytyt kysymykset kortin todennäköisyydestä
1. Mikä on kortin todennäköisyys?
Todennäköisyyttä nostaa kortti korttipakasta kutsutaan kortin todennäköisyydeksi.
2. Listaa korttipakan pukutyypit.
Korttipakassa on neljä erilaista maata. He ovat:
- Sydämiä
- Timantit
- Pata
- Klubit
3. Mikä on näytetila korttipakalle, kun korttipakasta vedetään yksi kortti?
Korttipakan näytetila, kun yksi kortti vedetään, sisältää 52 tulosta.
4. Kirjoita todennäköisyyden määrittämisen kaava.
Kaava todennäköisyyden löytämiseksi saadaan seuraavasta:
Tapahtuman todennäköisyys = myönteisten tapahtumien lukumäärä / tulosten kokonaismäärä
TAI
P(E) = n(E) / n(S)
5. Kuinka monta kasvokorttia on korttipakassa?
Korttipakassa on 12 kasvokorttia.
