Tiedämme a puu on epälineaarinen tietorakenne. Sillä ei ole rajoituksia lasten lukumäärälle. AMikä on täydellinen binaaripuu?

Täydellinen binääripuu on erityinen binääripuu, jossa kaikki puun tasot täytetään kokonaan paitsi alimman tason solmut, jotka täytetään mahdollisimman vasemmalta.

Täydellinen binääripuu

Jotkut täydellisen binaaripuun terminologiasta:

• Juuri – Solmu, jossa ei ole reunaa lähtöpäältä. Esimerkki -solmu A
• Lapsi – Solmua, jolla on jokin saapuva reuna, kutsutaan lapsiksi. Esimerkki – solmut B, F ovat A:n ja C:n lapsia.
• Sisarus – Solmut, joilla on sama vanhempi, ovat sisaruksia. Esimerkki - D, E ovat sisaruksia, koska heillä on sama vanhempi B.
• Solmun aste – Tietyn vanhemman lasten lukumäärä. Esimerkki: A:n aste on 2 ja C:n aste on 1. D:n aste on 0.
• Sisäiset/ulkoiset solmut – Lehtisolmut ovat ulkoisia solmuja ja muut kuin lehtisolmut sisäisiä solmuja.
• Taso – Laske polun solmut kohdesolmuun saavuttamiseksi. Esimerkki - Solmun D taso on 2, koska solmut A ja B muodostavat polun.
• Korkeus – Reunojen määrä kohdesolmuun saavuttamiseksi, juuri on korkeudella 0. Esimerkki – Solmun E korkeus on 2, koska sillä on kaksi reunaa juuresta.

Täydellisen binaaripuun ominaisuudet:

• Täydellisen binääripuun sanotaan olevan oikea binääripuu, jossa kaikilla lehdillä on sama syvyys.
• Täydellisessä binääripuussa solmujen lukumäärä syvyydessä d On 2 ^d .
• Täydellisessä binääripuussa n solmujen korkeus puun on log(n+1) .
• Kaikki tasot paitsi viimeinen taso ovat täysin täynnä.

Täydellinen binaaripuu vs täydellinen binääripuu:

Binääripuu, jonka korkeus on 'h' ja jolla on suurin määrä solmuja, on a täydellinen binäärinen puu.
Tietylle korkeudelle h , solmujen enimmäismäärä on 2 ^h+1 -1 .

A saattaa loppuun binääripuu, jonka korkeus on h, on täydellinen binääripuu korkeuteen asti h-1 , ja viimeisen tason elementit tallennetaan vasemmalta oikealle järjestyksessä.

Esimerkki 1:

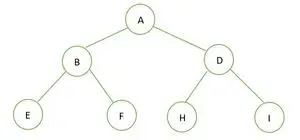
Binääripuu

Annetun binääripuun korkeus on 2 ja solmujen enimmäismäärä kyseisessä puussa on n= 2^h+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Tästä voimme päätellä, että se on täydellinen binääripuu .
Nyt täydellinen binääripuu, se on täynnä korkeuteen asti h-1 eli; 1, ja viimeiset tason elementit tallennetaan vasemmalta oikealle. Siksi se on myös täydellinen binaaripuu. Tässä on elementtien esitys, kun ne on tallennettu taulukkoon

Elementti tallennettu taulukkoon tasoittain

Matriisissa kaikki elementit tallennetaan jatkuvasti.

Esimerkki 2:

array lajitella java

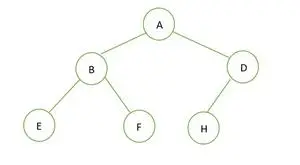
Binäärinen puu

Annetun binääripuun korkeus on 2 ja solmujen enimmäismäärä, jonka pitäisi olla, on 2^h+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Mutta solmujen lukumäärä puussa on 6 . Siksi se on ei täydellinen binääripuu .
Nyt täydellinen binääripuu, se on täynnä korkeuteen asti h-1 eli; 1 , ja viimeinen tason elementti tallennetaan vasemmalta oikealle. Siksi tämä on a täydellinen binääripuu . Tallenna elementti taulukkoon ja se on kuin;

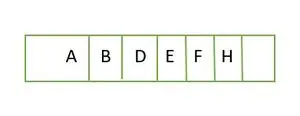
Elementti tallennettu taulukkoon tasoittain

Esimerkki 3:

kelvolliset tunnisteet javassa

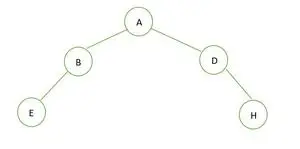
Binäärinen puu

Binääripuun korkeus on 2 ja siinä voi olla korkeintaan 7 solmua, mutta solmuja on vain 5, joten se on ei täydellinen binääripuu .
Täydellisen binääripuun tapauksessa näemme, että viimeisellä tasolla elementtejä ei täytetty vasemmalta oikealle. Niin se on ei täydellinen binääripuu .

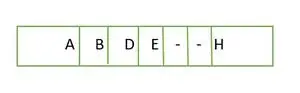
Elementti tallennettu taulukkoon tasoittain

Taulukon elementit eivät ole jatkuvia.

Täysi binaaripuu vs täydellinen binaaripuu:

Täydessä binääripuussa jokaisella solmulla on joko 2 lasta tai 0 lasta.

Esimerkki 1:

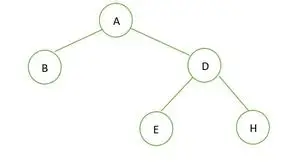
Binäärinen puu

Annetussa binääripuussa ei ole solmua, jolla on aste 1, joko 2 tai 0 lasta jokaiselle solmulle, joten se on täysi binääripuu .

Täydellisen binaaripuun elementit tallennetaan tasoittain eikä viimeisimmän tason vasemmalta puolelta. Siksi tämä on ei täydellinen binääripuu . Taulukon esitys on:

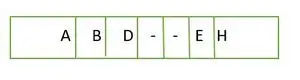
Elementti tallennettu taulukkoon tasoittain

Esimerkki 2:

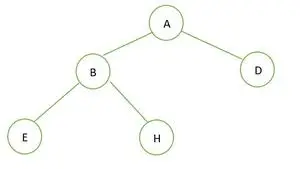
Binääripuu

Annetussa binääripuussa ei ole solmua, jonka aste on 1. Jokaisen solmun aste on joko 2 tai 0. Siksi se on täysi binääripuu .

Täydellisen binääripuun elementit tallennetaan taso kerrallaan ja täytetään viimeisen tason vasemmalta puolelta. Siksi tämä a täydellinen binääripuu . Alla on puun taulukkoesitys:

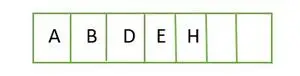
Elementti tallennettu taulukkoon tasoittain

Esimerkki 3:

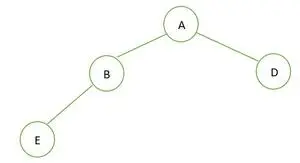
Binäärinen puu

Annetussa binääripuussa solmulla B on aste 1, mikä rikkoo täyden binääripuun ominaisuutta, joten se on ei täysi binaaripuu

vertaa merkkijonoja java

Täydellisen binääripuun elementit tallennetaan taso kerrallaan ja täytetään viimeisen tason vasemmanpuoleiselta puolelta. Siksi tämä on a täydellinen binääripuu . Binääripuun taulukkoesitys on:

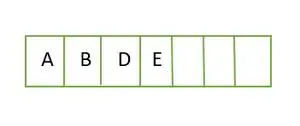
Elementti tallennettu taulukkoon tasoittain

Esimerkki 4:

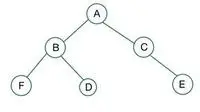
binäärinen puu

korvaa kaikki java

Annetussa binääripuun solmussa C on aste 1, mikä rikkoo täyden binääripuun ominaisuutta, joten se on ei täysi binaaripuu

Täydellisen binääripuun elementit tallennetaan taso kerrallaan ja täytetään viimeisen tason vasemmanpuoleiselta puolelta. Tässä solmu E rikkoo ehtoa. Siksi tämä on ei täydellinen binääripuu .

Täydellisen binaaripuun luominen:

Tiedämme a täydellinen binääripuu on puu, jossa viimeistä tasoa lukuun ottamatta (esim l )kaikella muulla tasolla on ( 2l ) solmut ja solmut ovat rivissä vasemmalta oikealle.
Se voidaan esittää taulukon avulla. Jos vanhempi on se hakemisto i joten vasen lapsi on klo 2i+1 ja oikea lapsi on 2i+2 .

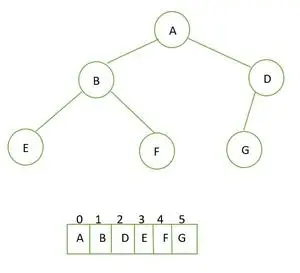
Täydellinen binääripuu ja sen taulukkoesitys

Algoritmi:

A:n luomiseen Täydellinen binääripuu , vaadimme a Vaihe 1: Alusta juuri uudella solmulla, kun puu on tyhjä.

Vaihe 2: Jos puu ei ole tyhjä, hanki etuelementti

• Jos etuelementillä ei ole vasenta alaosaa, aseta vasen lapsi uuteen solmuun
• Jos oikea lapsi ei ole läsnä, aseta oikea lapsi uudeksi solmuksi

Vaihe 3: Jos solmulla on molemmat lapset, niin pop se jonosta.

Vaihe 4: Aseta uudet tiedot jonoon.

Kuva:

Harkitse alla olevaa taulukkoa:

oho javassa

1. Ensimmäinen elementti on juuri (arvo indeksissä = 0 )

A otetaan juureksi

2. Seuraava elementti (indeksissä = 1 ) on vasen ja kolmas elementti (indeksi = 2 ) on oikea juuren lapsi

B vasen lapsi ja D oikea lapsi

3. neljäs (indeksi = 3 ) ja viides elementti (indeksi = 4 ) on B-solmun vasen ja oikea lapsi

E ja F ovat B:n vasen ja oikea lapsi

4. Seuraava elementti (indeksi = 5 ) jää solmun D lapseksi

G on D-solmun vasen lapsi

Näin luodaan täydellinen binääripuu.

Toteutus: Täydellisen binaaripuun rakentamista varten tasojärjestyksen läpikäyminen on annettu Tämä postaus .

Täydellisen binääripuun sovellus:

• Keon lajittelu
• Keon lajittelupohjainen tietorakenne

Tarkista, onko tietty binääripuu valmis vai ei: Seuraa Tämä postaus tarkistaaksesi, onko annettu binääripuu täydellinen vai ei.