Kompleksiluvut ovat reaalilukujen luonnollista jatkoa. Nykyaikana kompleksilukuja käytetään monilla aloilla, kuten digitaalisessa signaalinkäsittelyssä, kryptografiassa ja monilla tietokoneisiin liittyvillä aloilla.

Tässä artikkelissa opimme imaginaariluvuista, kompleksiluvuista ja niiden tyypeistä, erilaisista kompleksilukujen toiminnoista, kompleksilukujen ominaisuuksista, kompleksilukujen soveltamisesta jne.

Kompleksilukujen määritelmä

Monimutkaiset numerot ovat numeroita muodosta (a + i b) missä a & b ovat todellisia lukuja ja i on kuvitteellinen yksikkö nimeltä iota, joka edustaa √-1. Esimerkiksi 2 + 3i on kompleksiluku, jossa 2 on reaaliluku ja 3i on imaginaariluku. Kompleksiluvut voidaan kirjoittaa muodossa a + ib, missä a ja b ovat rationaalilukuja, jotka voidaan esittää numeroviivalla, joka ulottuu ääretön .

Kompleksiluvun moduuli

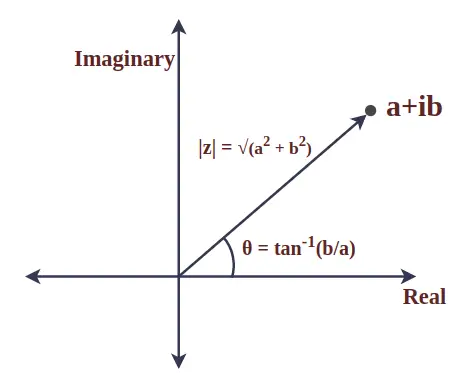
Kompleksiluvun moduuli on absoluuttinen arvo ja edustaa etäisyyttä origon ja annetun pisteen välillä. Se tunnetaan myös kompleksiluvun magnitudina. Tarkastellaan kompleksilukua z = a + ib, jolloin z:n moduuli määritellään seuraavasti:

|z| = √(a ² + b ² )

missä,

• a on kompleksiluvun z reaaliosa, ja
• b on kompleksiluvun z imaginaarinen osa.

Kompleksiluvun argumentti

Kompleksiluvun sädevektorin ja positiivisen x-akselin välistä kulmaa kutsutaan kompleksiluvun argumentiksi. Kompleksiluvulle z = a + ib se saadaan matemaattisesti seuraavasti:

θ = tan ^-1 (b/a)

missä,

• a on kompleksiluvun z reaaliosa, ja
• b on kompleksiluvun z imaginaarinen osa.

i(iota) voima

i(iota) määritellään -1:n neliöjuureksi. Siten mikä tahansa i:n potenssi voidaan ilmaista i:n toistuvana kertolaskuna itsestään, ts.

java esimerkki

• i = √(-1)
• i²= -1
• i³= – i
• i⁴= 1
• i⁵= i
• i⁶= -1
• ja niin edelleen..

Monimutkaisten lukujen tarve

Muinaisina aikoina ihmiset tiesivät vain luonnollisista luvuista sellaisina numeroita ovat luonteeltaan intuitiivisimpia, sillä ihmisaivoilla on jo käsitys niistä käyttämällä visuaalisia asioita, kuten lampaita ja ruokaa. Näin ollen meillä on vain joukko luonnollisia lukuja ( N ), mutta luonnollisissa luvuissa yhtälölle x + a = b (a> b) ja a, b ∈ N ei ole ratkaisua. Näin syntyi luonnollisten lukujen laajennus eli kokonaisluvut( minä ).

Nyt taas tässä lukujoukossa ei ole ratkaisua yhtälölle, ax = b (a ≠ 0) ja a, b ∈ I, missä a ja b ovat molemmat kokonaislukuja. Siten joukko kokonaislukuja (I) laajenee rationaalilukujen joukkoon ( K ).

Jälleen, tässä rationaalisten lukujen joukossa ei ole ratkaisua yhtälölle x²= a (a> 0) ja a ∈ Q. K on laajennettu sisältämään numerot siten, että x²= a(a> 0) eli irrationaaliset luvut. Tämä joukko on nimeltään Real Numbers ja sitä edustaa R .

Nyt ajateltiin pitkään, että meidän ei tarvitse laajentaa tätä reaalilukujoukkoa muodostaaksemme toisen suuremman joukon, koska tämä lukukokoelma näyttää olevan täydellinen. Mutta tässä lukujoukossa heräsi jälleen uusi ongelma, eli ei ole olemassa sellaista reaalilukua, että x²= a (a <0) ja a ∈ R. Siten reaalilukujen joukkoa laajennetaan edelleen sisältämään kaikki tällaiset arvotetut ja nimetyt kompleksiluvut, ja sitä edustaa C .

Kompleksilukujen luokitus

Kuten tiedämme, kompleksiluvun standardimuoto on z = (a + i b) missä a, b ∈ R ja i on iota (imaginaariyksikkö). Joten riippuen a:n (kutsutaan reaaliosaksi) ja b (kutsutaan imaginaariosaksi) arvoista, kompleksiluvut luokitellaan neljään tyyppiin:

• Nolla kompleksiluku
• Puhtaasti todellisia lukuja
• Puhtaasti kuvitteellisia numeroita
• Kuvitteellinen numero

Opitaanpa näistä tyypeistä yksityiskohtaisesti.

Nolla kompleksiluku

Minkä tahansa kompleksiluvun z = a + ib tapauksessa, jos a = 0 & b = 0, niin kompleksilukua kutsutaan nollakompleksiluvuksi. Esimerkiksi ainoa esimerkki tästä on 0.

Puhtaasti todellisia lukuja

Minkä tahansa kompleksiluvun z = a + ib tapauksessa, jos a ≠ 0 & b = 0, niin kompleksilukua kutsutaan puhtaasti reaaliluvuksi eli luvuksi, jossa ei ole imaginaariosaa. Kaikki reaaliluvut ovat esimerkkejä tästä, kuten 2, 3, 5, 7 jne.

Puhtaasti kuvitteellisia numeroita

Minkä tahansa kompleksiluvun z = a + ib tapauksessa, jos a = 0 & b ≠ 0, niin kompleksilukua kutsutaan puhtaasti imaginaariluvuksi eli luvuksi, jolla ei ole reaaliosaa. Kaikki luvut, joissa ei ole reaaliosia, ovat esimerkkejä tämäntyyppisistä luvuista, eli -7i, -5i, -i, i, 5i, 7i jne.

Kuvitteellinen numero

Mille tahansa kompleksiluvulle z = a + ib, jos a ≠ 0 & b ≠ 0, niin kompleksilukua kutsutaan kuvitteellinen luku . Esimerkiksi (-1 – i), (1 + i), (1 – i), (2 + 3i) jne.

Monimutkaisten lukujen eri muodot

On olemassa erilaisia ​​kompleksilukuja, jotka ovat

• Suorakaiteen muotoinen
• Polaarinen muoto
• Eksponentiaalinen muoto

Opitaanpa nyt niistä yksityiskohtaisesti.

Suorakaiteen muotoinen

Suorakaiteen muotoinen On kutsutaan myös Vakiolomake ja sitä edustaa (a + ib), jossa a ja b ovat reaalilukuja.

Esimerkiksi: (5 + 5i), (-7i), (-3 - 4i) jne.

Polaarinen muoto

Polaarinen muoto on kompleksiluvun esitys, jossa polaarikoordinaatit [jossa koordinaatit esitetään muodossa (r, θ), missä r on etäisyys origosta ja θ on pisteen ja origon yhdistävän suoran ja positiivisen x-akselin välinen kulma) käytetään edustamaan kompleksilukua. Mikä tahansa kompleksiluku esitetään muodossa r [cos θ + i sin θ].

Esimerkkejä: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] jne.

Eksponentiaalinen muoto

Kompleksilukujen eksponentiaaliset muodot on kompleksilukujen esitys käyttäen Eulerin kaavaa ja tässä muodossa kompleksilukua edustaa reⁱ, jossa r on pisteen etäisyys origosta ja θ on positiivisen x-akselin ja sädevektorin välinen kulma.

Esimerkkejä: e^minä(0), Se on^i(π/2), 5.e^i(π/6), jne.

Huomautus: Kaikki kolme edellä käsiteltyä kompleksilukujen muotoa ovat keskenään muunnettavissa, ts. ne voidaan muuntaa muodosta toiseen erittäin helposti.

Toiminnot kompleksiluvuilla

Kompleksiluvuille voidaan suorittaa seuraavat toiminnot:

• Lisäys
• Vähennyslasku
• Kertominen
• Division
• Konjugaatio

Kompleksinumeroiden lisääminen

Voimme lisätä kaksi kompleksilukua lisäämällä niiden reaali- ja imaginaariosat erikseen.

Esimerkiksi (3 + 2i) + (1 + 4i) = 4 + 6i.

Kompleksilukujen vähentäminen

Voimme vähentää kaksi kompleksilukua yksinkertaisesti vähentämällä niiden reaali- ja imaginaariosat erikseen.

Esimerkiksi (3 + 2i) – (1 + 4i) = 2 – 2i.

Monimutkaisten lukujen kertolasku

Voimme kertoa kaksi kompleksilukua käyttämällä distributiivista ominaisuutta ja sitä, että i²= -1.

Esimerkiksi (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Kompleksilukujen jako

Voimme jakaa yhden kompleksiluvun toisella yksinkertaisesti kertomalla sekä osoittajan että nimittäjän nimittäjän kompleksikonjugaatilla ja yksinkertaistamalla lauseketta entisestään.

Esimerkiksi (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Kompleksilukujen konjugointi

Löydämme helposti kompleksiluvun konjugaatti, yksinkertaisesti muuttamalla sen kuvitteellisen osan merkkiä. Kompleksiluvun konjugaattia merkitään usein pylvällä luvun yläpuolella, kuten z̄.

Esimerkiksi 3 + 2i:n konjugaatti on 3 – 2i.

Kompleksilukujen identiteetit

Mille tahansa kahdelle kompleksiluvulle z₁ja z₂seuraavat algebralliset identiteetit voidaan antaa:

• (Kanssa ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (Kanssa ₁ - Kanssa ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (Kanssa ₁ ) ² - (Kanssa ₂ ) ² = (z ₁ + z ₂ )(Kanssa ₁ - Kanssa ₂ )
• (Kanssa ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² Kanssa ₂ +3(z ₂ ) ² Kanssa ₁ + (z ₂ ) ³
• (Kanssa ₁ - Kanssa ₂ ) ³ = (z ₁ ) ³ – 3 (z ₁ ) ² Kanssa ₂ +3(z ₂ ) ² Kanssa ₁ - (Kanssa ₂ ) ³

Kompleksilukuihin liittyvät kaavat

Kompleksilukuihin liittyy joitain kaavoja, joista jotkin ovat seuraavat:

Eulerin kaava

Eulerin kaava näyttää eksponentin imaginaarisen tehon ja trigonometrisen suhteen sin ja cos välisen suhteen, ja se saadaan seuraavasti:

se on ^ix = cos x + i sin x

De Moivren kaava

De Moivren kaava ilmaisee n^thpolaarimuodossa olevan kompleksiluvun potenssi ja se saadaan kaavalla:

(cos x + i sin x) ⁿ = cos(nx) + i sin(nx)

Monimutkainen lentokone

Tasoa, jolla kompleksiluvut esitetään yksiselitteisesti, kutsutaan kompleksitasoksi tai Argandin tasoksi tai Gaussin tasoksi.

Kompleksitasossa on kaksi akselia:

• X-akseli tai todellinen akseli
• Y-akseli tai kuvitteellinen akseli

X-akseli tai todellinen akseli

• Kaikki puhtaasti todelliset kompleksiluvut esitetään yksiselitteisesti pisteellä.
• Kaikkien kompleksilukujen reaaliosa Re(z) piirretään sen suhteen.
• Siksi X-akselia kutsutaan myös nimellä Todellinen akseli .

Y-akseli tai kuvitteellinen akseli

• Kaikki puhtaasti imaginaariset kompleksiluvut esitetään yksiselitteisesti pisteellä.
• Kaikkien kompleksilukujen imaginaariosa Im(z) piirretään sen suhteen.
• Siksi Y-akselia kutsutaan myös nimellä Kuvitteellinen akseli .

Kompleksilukujen geometrinen esitys

Kuten tiedämme, jokaista kompleksilukua (z = a + i b) edustaa ainutlaatuinen piste p(a, b) kompleksitasolla ja jokainen kompleksitason piste edustaa ainutlaatuista kompleksilukua.

Jos haluat esittää mitä tahansa kompleksilukua z = (a + i b) kompleksitasolla, noudata näitä sopimuksia:

• Z:n reaaliosasta (Re(z) = a) tulee pisteen p X-koordinaatti

• z:n kuvitteellisesta osasta (Im(z) = b) tulee pisteen p Y-koordinaatti

Ja lopuksi z (a + i b) ⇒ p (a, b), joka on piste kompleksitasolla.

Kompleksilukujen ominaisuudet

Kompleksiluvuilla on useita ominaisuuksia, joista jotkin ovat seuraavat:

• Mille tahansa kompleksiluvulle z = a + ib, jos z = 0, niin a = 0 sekä b = 0.
• Neljälle reaaliluvulle a, b, c ja d siten, että z₁= a + ib ja z₂= c + id. Jos z₁= z₂silloin a = c ja b = d.
• Kompleksiluvun ja sen konjugaatin yhteenlaskemisesta saadaan puhtaasti reaaliluku, eli z + z̄ = Reaaliluku.

Olkoon z = a + ib,

leijuu css:ssä

z + z̄ = a + yksi + a – yksi

⇒ z + z̄ = 2a (joka on puhtaasti todellinen)

• Kompleksiluvun tulo konjugaattituloksineen on myös puhtaasti reaaliluku, eli z × z̄ = Reaaliluku

Olkoon sitten z = a + ib

z × z̄ = (a + yksi) × (a – yksi)

⇒ z × z̄= a²– i²b²

⇒ z × z̄ = a²+ b²(joka on puhtaasti totta)

• Kompleksiluvut ovat kommutatiivisia yhteen- ja kertolaskuoperaation alaisena. Tarkastellaan kahta kompleksilukua z₁ja z₂, ja sitten

Kanssa ₁ +z ₂ = z ₂ +z ₁

Kanssa ₁ × z ₂ = z ₂ × z ₁

• Kompleksiluvut ovat assosiatiivista yhteen- ja kertolaskuoperaatiolla. Tarkastellaan kolmea kompleksilukua z₁, Kanssa₂, ja z₃sitten

(Kanssa ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Kanssa ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Kompleksiluvut pitävät sisällään jakeluomaisuutta myös kertolaskua ja yhteenlaskua. Tarkastellaan kolmea kompleksilukua z₁, Kanssa₂, ja z₃sitten

Kanssa ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Lue lisää,

• Kompleksilukujen jakaminen
• Z-palkki kompleksiluvuissa

Esimerkkejä kompleksiluvuista

Esimerkki 1: Piirrä nämä kompleksiluvut z = 3 + 2i kompleksitasolla.

Ratkaisu:

Annettu:

Kanssa = 3 + 2 i

Joten piste on z(3, 2). Nyt piirrämme tämän pisteen alla olevaan kuvaajaan, tässä kaaviossa x-akseli edustaa reaaliosaa ja y-akseli edustaa imaginaarista osaa.

Esimerkki 2: Piirrä nämä kompleksiluvut z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 - 3 i), z ₄ = (1 – i) kompleksitasolla.

Ratkaisu:

Annettu:

Kanssa₁= (2 + 2 i)

Kanssa₂= (-2 + 3 i)

Kanssa₃= (-1 - 3 i)

Kanssa₄= (1-i)

Pisteet ovat siis z₁(2, 2), z₂(-2, 3), z₃(-1, -3) ja z₄(1, -1). Nyt piirrämme nämä pisteet alla olevaan kuvaajaan, tässä kaaviossa x-akseli edustaa reaaliosaa ja y-akseli edustaa imaginaariosaa.

Usein kysyttyä monimutkaisista numeroista

Määrittele kompleksiluvut.

Muodosta a+ib olevia lukuja kutsutaan kompleksiluvuiksi, joissa a ja b ovat reaaliluku ja i on imaginaariyksikkö, joka edustaa -1:n neliöjuurta.

Mitä eroa on reaaliluvulla ja kompleksiluvulla?

Ero todellisten ja kompleksilukujen välillä on, että tarvitsemme vain yhden luvun edustamaan mitä tahansa reaalilukua, mutta tarvitsemme kaksi reaalilukua edustamaan mitä tahansa kompleksilukua.

Mikä on kompleksiluvun reaaliosa ja imaginaariosa?

Kompleksiluvussa a + ib a on kompleksiluvun reaaliosa ja b:tä kutsutaan kompleksiluvun imaginaariosaksi.

Mikä on kompleksiluvun kompleksikonjugaatti?

Kompleksiluvun a + ib kohdalla a – ib kutsutaan sen kompleksikonjugaatiksi. Monimutkaiset konjugaatit löytyvät yksinkertaisesti muuttamalla imaginaariosan etumerkkiä.

Mikä on kompleksiluvun moduuli?

Etäisyyttä origon ja kompleksiluvun edustaman pisteen välillä argand-tasossa kutsutaan kyseisen kokonaisluvun moduuliksi ja z = a + ib se saadaan matemaattisesti kaavalla:

|z| = √(a ² + b ² )

Mikä on kompleksiluvun argumentti?

Kompleksiluvun sädevektorin ja positiivisen x-akselin välistä kulmaa kutsutaan kompleksiluvun argumentiksi ja jos z = a + ib, se saadaan matemaattisesti seuraavasti:

θ = tan ^-1 (b/a)

Mikä on kompleksiluvun polaarinen muoto?

Minkä tahansa kompleksiluvun, z = a + ib, polaarinen muoto saadaan seuraavasti:

r [cos θ + i sin θ]

Mikä on Eulerin kaava?

Eulerin kaava näyttää eksponentin imaginaarisen tehon ja trigonometrisen suhteen sin ja cos välisen suhteen, ja se saadaan seuraavasti:

se on ^ix = cos x + i sin x