COTANGENT FORMULA - TECHCODEVIEW.COM

Trigonometria on tärkeä matematiikan haara, joka käsittelee suorakulmaisen kolmion sivujen pituuksien ja kulmien välistä suhdetta. Sini, kosini, tangentti, kosekantti, sekantti ja kotangentti ovat kuusi trigonometristä suhdetta tai funktiota. Kun trigonometrinen suhde on kuvattu suorakulmaisen kolmion sivujen välisenä suhteena.

sin θ = vastakkainen puoli/hypotenuusa
cos θ = viereinen sivu/hypotenuusa
tan θ = vastakkainen puoli / viereinen puoli
cosec θ = 1/sin θ = hypotenuusa/vastakkainen puoli
sec θ = 1/cos θ = hypotenuusa / viereinen puoli
pinnasänky θ = 1/rusketus θ = viereinen puoli/vastakkainen puoli

Kotangentin kaava

Kotangenttifunktio on annetun tangenttifunktion käänteisfunktio. Suorakulmaisen kolmion kotangenttikulman arvo on annetun kulman vieressä olevan sivun pituuden suhde annettua kulmaa vastakkaisen sivun pituuteen. Kirjoitamme kotangentin funktiona cot.

Kolmio ABC

Nyt kulman θ kotangenttikaava on,

pinnasänky θ = (viereinen puoli)/(vastakkainen puoli)

Kotangenttifunktio on positiivinen ensimmäisessä ja kolmannessa kvadrantissa ja negatiivinen toisessa ja neljännessä neljänneksessä.

pinnasänky (2π + θ) = pinnasänky θ (1^stkvadrantti)
pinnasänky (π – θ) = – pinnasänky θ (2^ndkvadrantti)
pinnasänky (π + θ) = pinnasänky θ (3^rdkvadrantti)
pinnasänky (2π – θ) = – pinnasänky θ (4^thkvadrantti)

Kotangenttifunktio on negatiivinen funktio, koska negatiivisen kulman kotangentti on kotangentin positiivisen kulman negatiivinen.

pinnasänky (-θ) = – pinnasänky θ

Tangenttifunktion suhteen kotangenttifunktio kirjoitetaan seuraavasti,

pinnasänky θ = 1/tan θ

(tai)

pinnasänky θ = rusketus (90° – θ) (tai) rusketus (π/2 – θ)

Kotangenttifunktio sini- ja kosinifunktioiden suhteen voidaan kirjoittaa seuraavasti,

cot θ = cos θ/sin θ

Tiedämme, että pinnasänky θ = viereinen puoli/vastakkainen puoli

Jaa nyt sekä osoittaja että nimittäjä hypotenuusalla

⇒ pinnasänky θ = (viereinen puoli/hypotenuusa) / (vastakkainen puoli/hypotenuusa)

Tiedämme, että sin θ = vastakkainen puoli/hypotenuusa

cos θ = viereinen sivu/hypotenuusa

Siten cot θ = cos θ/sin θ

Kotangenttifunktio sinifunktiona voidaan kirjoittaa seuraavasti,

pinnasänky θ = (√1 – sin ² i)/synti i

Tiedämme, että cot θ = cos θ/sin θ

Pythagoralaisista identiteeteistä, joita meillä on;

cos²θ + synti²θ = 1

⇒ cos θ = √1 – sin²i

Siten pinnasänky θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Kotangenttifunktio kosinifunktiona voidaan kirjoittaa seuraavasti,

pinnasänky θ = cos θ/(√1 -cos ² i)
luettelon hakemisto

Tiedämme, että cot θ = cos θ/sin θ

Pythagoralaisista identiteeteistä, joita meillä on;

cos²θ + synti²θ = 1

sin θ = √1 – cos²i

Siten pinnasänky θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Sekantti- ja kosekanttifunktioiden kotangenttifunktio voidaan kirjoittaa seuraavasti,

cot θ = cosec θ/sec θ

Meillä on, cot θ = cos θ/sin θ

Tämä voidaan kirjoittaa seuraavasti: cot θ = (1/sin θ) / (1/cos θ)

⇒ pinnasänky θ = kosek θ/s θ

Kotangenttifunktio kosekanttifunktiona voidaan kirjoittaa seuraavasti:

pinnasänky θ = √(kosek ² - 1)

Pythagoralaisista identiteeteistä meillä on

cosec²θ – pinnasänky²θ = 1

⇒ pinnasänky²θ = 1 – kosek²- 1

Siten pinnasänky θ = √(kosek²- 1)

Sekanttifunktion kotangenttifunktio voidaan kirjoittaa seuraavasti:

pinnasänky θ = 1/(√s ² minä - 1)

Pythagoralaisista identiteeteistä meillä on

sek²θ – niin²θ = 1

tan θ = √s²minä - 1

Tiedämme, että pinnasänky θ = 1/tan θ

Siten, pinnasänky θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Trigonometrinen suhdetaulukko

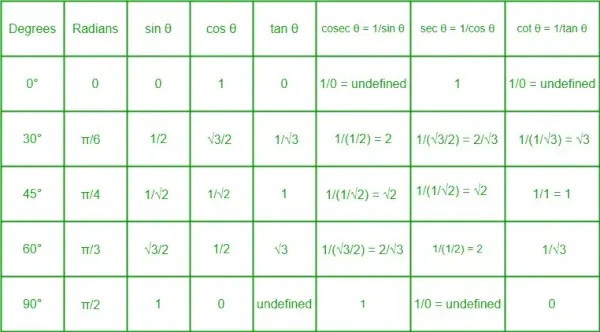
Trigonometrinen suhdetaulukko

Kotangentin laki tai kotangenttien laki

Kotangenttilaki näyttää samanlaiselta kuin sinilaki, mutta tässä se sisältää puolikulmia. Kotangenttien laki kuvaa kolmion sivujen pituuksien ja kolmen kulman puoliskojen kotangenttien välistä suhdetta. Tarkastellaan kolmiota ABC, jossa a, b ja c ovat kolmion sivujen pituudet.

Kotangenttien laki sanoo, että

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Missä s on kolmion ABC puolikehä ja r on sen kolmion piirretyn ympyrän säde.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Esimerkkiongelmat

Tehtävä 1: Etsi sängyn θ arvo, jos tan θ = 3/4.

Ratkaisu:

Annetut tiedot tan θ = 3/4

Tiedämme sen, pinnasänky θ = 1/tan θ

⇒ pinnasänky θ = 1/(3/4) = 4/3

Joten pinnasänky θ = 4/3

Tehtävä 2: Etsi cot α, sin α = 1/3 ja cos α = 2√2/3 arvo.

konekirjoitussarja

Ratkaisu:

Annetut tiedot sin α = 1/3 ja cos α = 2√2/3

Tiedämme sen, pinnasänky α = cos α/sin α

⇒ pinnasänky α = (2√2/3) / (1/3) = 2√2

Siten pinnasängyn arvo α = 2√2

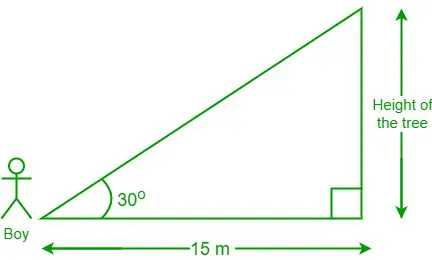
Tehtävä 3: Poika, joka seisoo 15 metrin päässä puusta, katsoo 30 asteen kulmassa puun latvaan. Mikä on puun korkeus?

Ratkaisu:

Kaavio annetuista tiedoista

Annetuilla tiedoilla pojan ja puun jalan välinen etäisyys = 15 m ja θ = 30°

Olkoon puun korkeus 'h'

Meillä on, pinnasänky θ = viereinen puoli/vastakkainen puoli

⇒ pinnasänky 30° = 15/h

⇒ √3 = 15/h [koska, pinnasänky 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Näin ollen puun korkeus = 5√3 m

Tehtävä 4: Etsi pinnasänky x:n arvo, jos sek x = 6/5.

Ratkaisu:

Annetut tiedot, sek x = 6/5

Meillä on, sek ² x - niin ² x = 1

⇒ (6/5)²-niin²x = 1

⇒ 36/25 – niin²x = 1

⇒ niin²x = 36/25 – 1

⇒ niin²x = 11/25

⇒ tan x = √(11/25) = √11/5

Tiedämme sen, pinnasänky x = 1/rusketus x

⇒ pinnasänky x = 1/(√11/5) = 5/√11

Siten pinnasänky x = 5/√11

Tehtävä 5: Etsi cot θ:n arvo, jos cosec θ = 25/24.

Ratkaisu:

Annetut tiedot, cosec θ = 25/24

Tiedämme sen, pinnasänky θ = √(kosek ² - 1)

⇒ pinnasänky θ = √(25/24)²- 1

⇒ pinnasänky θ = √(625 – 576)/576 = √49/576

⇒ pinnasänky θ = 7/24

Siten pinnasänky θ = 7/24

Tehtävä 6: Etsi pinnasängyn β arvo, jos sin β = 5/13.

Ratkaisu:

Annetuilla tiedoilla sin β = 5/13

Tiedämme sen, ilman ² β + cos ² β = 1

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

pinnasänky β = cosβ/sin β

= (12/13) / (5/13)

⇒ pinnasänky β = 12/5

Siten pinnasänky β = 12/5

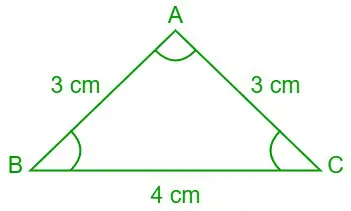
Tehtävä 7: Etsi kotangenttien lain avulla arvot ∠A, ∠B ja ∠C (asteina), jos kolmion ABC kolmen sivun pituudet ovat a = 4 cm, b= 3 cm ja c= 3 cm.

Ratkaisu:

Annettu a = 4 cm, b = 3 cm ja c = 3 cm

Kolmio ABC

Kotangenttien laista,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Nyt s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Kolmion säde r = 2/√5

Kotangenttien lain yhtälöstä,

pinnasänky (A/2)/1 = 1/(2/√5)

⇒ pinnasänky (A/2) = √5/2 ⇒ A/2 = pinnasänky^-1(√5/2)
verkkoselaimen asetukset

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

pinnasänky (B/2)/2 = 1/(2/√5)

⇒ pinnasänky(B/2)/2 = √5/2 ⇒ pinnasänky (B/2) = √5

⇒ (B/2) = pinnasänky^-1(√5) = 24,1° ⇒ ∠B = 48,2°

pinnasänky (C/2)/2 = 1/(2/√5)

⇒ pinnasänky(C/2) = √5 ⇒ (C/2) = pinnasänky^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Näin ollen kolmion ABC kulmat ovat ∠A = 83,6°, ∠B = 48,2° ja ∠C = 48,2°.