Euklidinen algoritmi on tapa löytää kahden positiivisen kokonaisluvun suurin yhteinen jakaja. Kahden luvun GCD on suurin luku, joka jakaa ne molemmat. Yksinkertainen tapa löytää GCD on kertoa molemmat luvut ja kertoa yleiset alkutekijät.
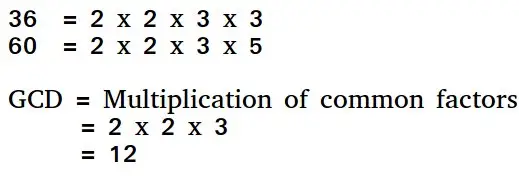
Euklidinen perusalgoritmi GCD:lle:
Algoritmi perustuu alla oleviin faktoihin.
- Jos vähennämme pienemmän luvun suuremmasta (vähennämme suurempaa lukua), GCD ei muutu. Joten jos vähennämme toistuvasti kahdesta suuremman, päädymme GCD:hen.
- Nyt vähennyksen sijaan, jos jaamme pienemmän luvun, algoritmi pysähtyy, kun löydämme jäännöksen 0.
Alla on rekursiivinen funktio gcd:n arvioimiseksi Euclidin algoritmilla:
C
// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 35, b = 10;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 31, b = 2;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >return> 0;> }> |
>
>
CPP
// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 35, b = 10;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 31, b = 2;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >return> 0;> }> |
>
java-indeksi
>
Java
// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a ==>0>)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver code> >public> static> void> main(String[] args)> >{> >int> a =>10>, b =>15>, g;> > >// Function call> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>35>;> >b =>10>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>31>;> >b =>2>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // Code Contributed by Mohit Gupta_OMG> |
>
>
Python 3
# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> >if> a>=>=> 0>:> >return> b> >return> gcd(b>%> a, a)> # Driver code> if> __name__>=>=> '__main__'>:> >a>=> 10> >b>=> 15> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 35> >b>=> 10> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 31> >b>=> 2> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> # Code Contributed By Mohit Gupta_OMG> |
>
>
C#
// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver Code> >static> public> void> Main()> >{> >int> a = 10, b = 15, g;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 35;> >b = 10;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 31;> >b = 2;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // This code is contributed by ajit> |
>
>
PHP
// php program to demonstrate Basic Euclidean Algorithm> // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) { if ($a == 0) return $b; return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ', gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ', gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ', gcd($a, $b); // This code is contributed by m_kit ?>>> |
>lista merkkijono java
// JavaScript program to demonstrate>// Basic Euclidean Algorithm>// Function to return>// gcd of a and b>function>gcd( a, b)>{>>if>(a == 0)>>return>b;>>return>gcd(b % a, a);>}>// Driver Code>>let a = 10, b = 15;>>document.write(>'GCD('>+ a +>', '>>+ b +>') = '>+ gcd(a, b) +>' '>);>>>a = 35, b = 10;>>document.write(>'GCD('>+ a +>', '>>+ b +>') = '>+ gcd(a, b) +>' '>);>>>a = 31, b = 2;>>document.write(>'GCD('>+ a +>', '>>+ b +>') = '>+ gcd(a, b) +>' '>);>// This code contributed by aashish1995>>>LähtöGCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1>Aika monimutkaisuus: O(Loki min(a, b))
Aputila: O(Loki (min(a,b))Laajennettu euklidinen algoritmi:
Laajennettu euklidinen algoritmi löytää myös kokonaislukukertoimet x ja y siten, että: ax + by = gcd(a, b)
Esimerkkejä:
Syöte: a = 30, b = 20
Lähtö: gcd = 10, x = 1, y = -1
(Huomaa, että 30*1 + 20*(-1) = 10)Syöte: a = 35, b = 15
Lähtö: gcd = 5, x = 1, y = -2
(Huomaa, että 35*1 + 15*(-2) = 5)Laajennettu euklidinen algoritmi päivittää gcd(a, b):n tulokset käyttämällä rekursiivisen kutsun gcd(b%a, a) laskemia tuloksia. Olkoon rekursiivisen kutsun laskemat x:n ja y:n arvot x1ja y1. x ja y päivitetään alla olevilla lausekkeilla.
Suositeltu käytännön laajennettu euklidinen algoritmi Kokeile!ax + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x1+ on1
ax + by = (b%a)x1+ on1
ax + by = (b – [b/a] * a)x1+ on1
ax + by = a(y1– [b/a] * x1) + bx1LHS:n ja RHS:n vertailu
x = y1– ?b/a? *x1
y = x1Alla on yllä olevan lähestymistavan toteutus:
C++
// C++ program to demonstrate working of>// extended Euclidean Algorithm>#include>using>namespace>std;>// Function for extended Euclidean Algorithm>int>gcdExtended(>int>a,>int>b,>int>*x,>int>*y)>{>>// Base Case>>if>(a == 0)>>{>>*x = 0;>>*y = 1;>>return>b;>>}>>int>x1, y1;>// To store results of recursive call>>int>gcd = gcdExtended(b%a, a, &x1, &y1);>>// Update x and y using results of>>// recursive call>>*x = y1 - (b/a) * x1;>>*y = x1;>>return>gcd;>}>// Driver Code>int>main()>{>>int>x, y, a = 35, b = 15;>>int>g = gcdExtended(a, b, &x, &y);>>cout <<>'GCD('><< a <<>', '><< b>><<>') = '><< g << endl;>>return>0;>}>>>C
// C program to demonstrate working of extended>// Euclidean Algorithm>#include>// C function for extended Euclidean Algorithm>int>gcdExtended(>int>a,>int>b,>int>*x,>int>*y)>{>>// Base Case>>if>(a == 0)>>{>>*x = 0;>>*y = 1;>>return>b;>>}>>int>x1, y1;>// To store results of recursive call>>int>gcd = gcdExtended(b%a, a, &x1, &y1);>>// Update x and y using results of recursive>>// call>>*x = y1 - (b/a) * x1;>>*y = x1;>>return>gcd;>}>// Driver Program>int>main()>{>>int>x, y;>>int>a = 35, b = 15;>>int>g = gcdExtended(a, b, &x, &y);>>printf>(>'gcd(%d, %d) = %d'>, a, b, g);>>return>0;>}>>>Java
// Java program to demonstrate working of extended>// Euclidean Algorithm>import>java.lang.*;>import>java.util.*;>class>GFG {>>// extended Euclidean Algorithm>>public>static>int>gcdExtended(>int>a,>int>b,>int>x,>>int>y)>>{>>// Base Case>>if>(a ==>0>) {>>x =>0>;>>y =>1>;>>return>b;>>}>>int>x1 =>1>,>>y1 =>1>;>// To store results of recursive call>>int>gcd = gcdExtended(b % a, a, x1, y1);>>// Update x and y using results of recursive>>// call>>x = y1 - (b / a) * x1;>>y = x1;>>return>gcd;>>}>>// Driver Program>>public>static>void>main(String[] args)>>{>>int>x =>1>, y =>1>;>>int>a =>35>, b =>15>;>>int>g = gcdExtended(a, b, x, y);>>System.out.print(>'gcd('>+ a +>' , '>+ b>>+>') = '>+ g);>>}>}>>>Python 3
# Python program to demonstrate working of extended># Euclidean Algorithm># function for extended Euclidean Algorithm>def>gcdExtended(a, b):>># Base Case>>if>a>=>=>0>:>>return>b,>0>,>1>>gcd, x1, y1>=>gcdExtended(b>%>a, a)>># Update x and y using results of recursive>># call>>x>=>y1>->(b>/>/>a)>*>x1>>y>=>x1>>return>gcd, x, y># Driver code>a, b>=>35>,>15>g, x, y>=>gcdExtended(a, b)>print>(>'gcd('>, a,>','>, b,>') = '>, g)>>>C#
// C# program to demonstrate working>// of extended Euclidean Algorithm>using>System;>class>GFG>{>>>// extended Euclidean Algorithm>>public>static>int>gcdExtended(>int>a,>int>b,>>int>x,>int>y)>>{>>// Base Case>>if>(a == 0)>>{>>x = 0;>>y = 1;>>return>b;>>}>>// To store results of>>// recursive call>>int>x1 = 1, y1 = 1;>>int>gcd = gcdExtended(b % a, a, x1, y1);>>// Update x and y using>>// results of recursive call>>x = y1 - (b / a) * x1;>>y = x1;>>return>gcd;>>}>>>// Driver Code>>static>public>void>Main ()>>{>>int>x = 1, y = 1;>>int>a = 35, b = 15;>>int>g = gcdExtended(a, b, x, y);>>Console.WriteLine(>'gcd('>+ a +>' , '>+>>b +>') = '>+ g);>>}>}>>>PHP
// PHP program to demonstrate // working of extended // Euclidean Algorithm // PHP function for // extended Euclidean // Algorithm function gcdExtended($a, $b, $x, $y) { // Base Case if ($a == 0) { $x = 0; $y = 1; return $b; } // To store results // of recursive call $gcd = gcdExtended($b % $a, $a, $x, $y); // Update x and y using // results of recursive // call $x = $y - floor($b / $a) * $x; $y = $x; return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>>>np.argmax>
>// Javascript program to demonstrate>// working of extended>// Euclidean Algorithm>// Javascript function for>// extended Euclidean>// Algorithm>function>gcdExtended(a, b,>>x, y)>{>>// Base Case>>if>(a == 0)>>{>>x = 0;>>y = 1;>>return>b;>>}>>// To store results>>// of recursive call>>let gcd = gcdExtended(b % a,>>a, x, y);>>// Update x and y using>>// results of recursive>>// call>>x = y - (b / a) * x;>>y = x;>>return>gcd;>}>// Driver Code>let x = 0;>let y = 0;>let a = 35;>let b = 15;>let g = gcdExtended(a, b, x, y);>document.write(>'gcd('>+ a);>document.write(>', '>+ b +>')'>);>document.write(>' = '>+ g);>>>>Lähtö:
gcd(35, 15) = 5>Aika monimutkaisuus: O(log N)
Aputila: O(log N)Miten laajennettu algoritmi toimii?
Kuten yllä näkyy, x ja y ovat tuloksia syötteille a ja b,
a.x + b.y = gcd —-(1)
Ja x1ja y1ovat tuloksia syötteille b%a ja a
(b%a).x1+ a.y1= gcd
Kun laitamme yllä olevaan kohtaan b%a = (b – (?b/a?).a),
saamme perässä. Huomaa, että ?b/a? on kerros (b/a)(b – (?b/a?).a).x1+ a.y1= gcd
Yllä oleva yhtälö voidaan kirjoittaa myös seuraavasti
b.x1+ a.(ja1– (?b/a?).x1) = gcd — (2)
Sen jälkeen kun on vertailtu kertoimia 'a' ja 'b' kohdassa (1) ja
(2), seuraamme,
x = y1– ?b/a? *x1
y = x1Miten laajennettu algoritmi on hyödyllinen?
Laajennettu euklidinen algoritmi on erityisen hyödyllinen, kun a ja b ovat koprime (tai gcd on 1). Koska x on a modulo b:n modulaarinen kertova käänteisluku ja y on b:n modulo a:n modulaarinen kertova käänteisluku. Erityisesti modulaarisen multiplikatiivisen käänteisarvon laskenta on olennainen vaihe RSA:n julkisen avaimen salausmenetelmässä.
