Regressio- ja todennäköisyysluokitusongelmat voidaan ratkaista käyttämällä Gaussin prosessia (GP), valvottua oppimistekniikkaa. Koska jokainen Gaussin prosessi voidaan ajatella monimuuttujan äärettömänä ulotteisena yleistyksenä Gaussin jakaumat , termi Gaussian esiintyy nimessä. Keskustelemme tässä viestissä Gaussin regression prosesseista, joita kutsutaan myös Gaussin prosessiregressioksi (GPR). Lukuisia materiaalitieteen, kemian, fysiikan ja biologian alan ongelmia on ratkaistu GPR:n avulla.
Sisällysluettelo
- Gaussin prosessin regressio (GPR)
- Gaussin prosessiregression (GPR) keskeiset käsitteet
- Gaussin prosessiregression (GPR) matemaattinen käsite
- Gaussin prosessin toteutus Pythonissa
Gaussin prosessin regressio (GPR)
Gaussin prosessiregressio (GPR) on tehokas ja joustava ei-parametrinen regressiotekniikka, jota käytetään koneoppiminen ja tilastot . Se on erityisen hyödyllinen käsiteltäessä ongelmia, joihin liittyy jatkuvaa dataa, kun tulomuuttujien ja tulosteen välistä suhdetta ei tunneta tarkasti tai se voi olla monimutkainen. GPR on Bayesin lähestymistapa, joka voi mallintaa ennusteiden varmuutta, mikä tekee siitä arvokkaan työkalun erilaisiin sovelluksiin, kuten optimointiin, aikasarjaennusteisiin ja muihin. GPR perustuu Gaussin prosessin käsitteeseen, joka on kokoelma satunnaismuuttujia, joiden millä tahansa äärellisellä määrällä on yhteinen Gaussin jakauma. Gaussin prosessia voidaan pitää funktioiden jakaumana.
Gaussin prosessiregression (GPR) keskeiset käsitteet
Gaussainin prosessi
Ei-parametrinen, todennäköisyysmalli, nimeltään a Gaussin prosessi (GP) käytetään tilastoissa ja koneoppimisessa regressioon, luokitukseen ja epävarmuuden kvantifiointiin. Se kuvaa ryhmän satunnaismuuttujia, joilla jokaisella on yhteinen Gaussin jakauma ja joilla voi olla äärellinen luku. Yleislääkärit ovat monipuolinen ja tehokas tekniikka tietojen monimutkaisten suhteiden mallintamiseen ja ennusteiden tuottamiseen, joihin liittyy epävarmuutta.
Gaussin prosessien ominaisuudet :
java perintö
- Ei-parametrinen luonne : Yleislääkärit voivat mukautua tietojen monimutkaisuuteen, koska he eivät luota tiettyyn määrään malliparametreja
- Todennäköisyysennusteet : Yleislääkärien ennusteet voidaan kvantifioida, koska ne toimittavat ennusteita todennäköisyysjakaumina.
- Interpolointi ja tasoitus : GP:t ovat hyödyllisiä kohinaisille tai epäsäännöllisille näytteille, koska ne ovat hyviä tasoittamaan kohinaisia tietoja ja interpoloimaan datapisteiden välillä.
- Hyperparametrien marginalisointi : Poistamalla vaatimuksen nimenomaisesta hyperparametrien säätämisestä ne marginalisoivat hyperparametrit, mikä tekee mallista yksinkertaisemman.
Keskimääräinen toiminto
Kussakin tulopisteessä mallinnettavan funktion ennustettua arvoa edustaa keskimääräinen toiminto Gaussin prosesseissa (GPs). Se toimii perustavanlaatuisena oletuksena taustalla olevasta tietorakenteesta. Keskiarvofunktio asetetaan usein oletuksena nollaan, ei välttämättä, ja sitä voidaan muokata tietojen ominaisuuksien tai toimialueen asiantuntemuksen perusteella. Ennusteiden keskeiseen suuntaukseen vaikuttamalla se auttaa yleislääkäreitä tunnistamaan tiedosta malleja tai trendejä. Yleislääkärit tarjoavat todennäköisyysennusteita, jotka sisältävät epävarmuutta, sekä pisteestimaatteja sisällyttämällä mukaan keskiarvon
Kovarianssi (ydin) -funktio
The kovarianssifunktio , jota kutsutaan myös ydinfunktioksi, mittaa, kuinka samankaltaisia tulodatapisteet ovat keskenään Gaussin prosesseissa (GPs). Se on olennainen GP-mallin käyttäytymisen karakterisoinnissa, mikä vaikuttaa edellisen jakauman funktioiden valintaan. Kovarianssifunktio mittaa pareittain yhtäläisyyksiä funktion arvojen välisen korrelaation varmistamiseksi. GP:t voivat mukautua monenlaisiin tietokuvioihin sujuvasta trendistä monimutkaisiin rakenteisiin, koska eri ytimen toiminnot sieppaavat erilaisia korrelaatioita. Ytimen valinta voi vaikuttaa suuresti mallin suorituskykyyn.
Aiemmat jakelut
The aiempi jakelu , Gaussin prosesseissa (GPs), on ymmärryksemme toiminnoista ennen tietojen havainnointia. Yleensä sitä kuvataan kovarianssifunktiolla (ydin) ja keskiarvofunktiolla. Kovarianssifunktio kuvaa samankaltaisuutta tai korrelaatiota funktioarvojen välillä eri syöttöpisteissä, kun taas keskiarvofunktio koodaa aikaisemmat odotuksemme. Yleislääkärit käyttävät tätä etukäteen luodakseen funktioiden jakautumisen. Yleislääkäreissä priorit voidaan valita edustamaan tietojen epävarmuutta, integroimaan aluetietoa tai osoittamaan sujuvuutta.
Jälkijakaumat
Gaussin prosessit myöhempää jakelua näyttää tarkistetut oletuksemme funktioista datan havainnoinnin jälkeen. Se kokoaa yhteen datan todennäköisyyden funktion ja edellisen jakauman perusteella. GP-regression posteriori tarjoaa jakauman funktioille, jotka vastaavat eniten havaittuja tietoja. Sallimalla todennäköisyysennusteet ja epävarmuuden kvantifioinnin, jälkijakauma heijastaa kompromissia aikaisempaan jakaumaan tallennettujen aikaisempien uskomusten ja datan tuottaman tiedon välillä.
Gaussin prosessiregression (GPR) matemaattinen käsite
Regressiotehtävissä käytetään ei-parametrista todennäköisyyspohjaista koneoppimismallia, jota kutsutaan Gaussin prosessin (GP) regressioksi. Kun mallinnetaan monimutkaisia ja moniselitteisiä vuorovaikutuksia tulo- ja lähtömuuttujien välillä, se on tehokas työkalu. Monimuuttujan Gaussin jakauman oletetaan tuottavan datapisteet GP-regressiossa, ja tavoitteena on päätellä tämä jakauma.
GP-regressiomallilla on seuraava matemaattinen lauseke. Oletetaan x1, x2,…..,xnovat syötetietopisteet , joissa x kuuluvat reaalilukuihin (-2,-1,0,1…), (xi
Oletetaan y1, ja2 ,……., janovat lähtöarvot, missä yikuuluu reaalilukuun (yi
GP-regressiomallissa oletetaan, että Gaussin prosessi, jolla on keskiarvofunktio (
Sitten testipaikkojen x* joukossa f:n jakauma saadaan seuraavasti:
Tyypillisesti ydinfunktioita käytetään määrittelemään keskiarvofunktio ja kovarianssifunktio. Esimerkkinä usein käytetty neliöllinen eksponentiaalinen ydin on kuvattu seuraavasti:
Missä,
k(x_{i}, x_{j}) = Tämä edustaa ydinfunktiota ja se laskee korrelaation tai samankaltaisuuden kahden syötetietopisteen välillä, xija xj.sigma^2 = Ytimen varianssiparametri on tämä. Se määrittää ydinfunktion mittakaavan tai vertikaalisen leviämisen. Se säätelee, kuinka voimakkaasti datapisteet korreloivat. Korkeampisigma^2 tuottaa ytimen funktion, jolla on suurempi varianssi.- exp: Eksponentiaalinen funktio on vastuussa e:n nostamisesta argumentin potenssiin.
||x_{i} – x_{j}||^2 : syöttötietopisteiden välinen ero, xija xj, on Euklidisen etäisyyden neliö. Piirreavaruuden pisteiden välinen geometrinen erotus mitataan.- l2: Tämä on esitys ytimen pituusasteikosta tai ominaispituudesta. Se säätelee nopeutta, jolla ydintoiminto heikkenee, kun datapisteet ovat kauempana toisistaan. Alempi l saa ytimen hajoamaan nopeammin.
GP-regressiomalli soveltaa Bayesin päättelyä määrittämään f:n jakauman, joka todennäköisimmin on tuottanut datan harjoitusdatajoukon (x, y) perusteella. Tätä varten on laskettava f:n posteriorijakauma annetulla tiedolla, joka määritellään seuraavasti:
rekisterin siirtologiikka
jossa datan marginaalitodennäköisyys on p(y|x), f:n ennakkojakauma on p(f) ja funktiolla f annetun datan todennäköisyys on (y|x,f).
Kun malli on oppinut f:n posteriorijakauman, se laskee posteriorisen ennustavan jakauman tehdäkseen ennusteita lisätestipisteissä x*. Se voidaan määritellä seuraavasti:
Missä,
p(f^*|x*, y, x) = Tämä näyttää, ottaen huomioon harjoitustiedot y ja x, ennustettujen funktioarvojen f ehdollisen todennäköisyyden*uudessa syöttöpisteessä x*Toisin sanoen se on todennäköisyysjakauma kaikkien mahdollisten funktioarvojen välillä uudessa syöttökohdassa x*, joka on sidottu havaittuun dataan y ja niiden vastaaviin syöttökohtiin x.int p(f^*|x^*, f)p(f|y,x)df = Integraalia käytetään tässä yhtälön osassa määrittämään ehdollinen todennäköisyys. Integraali sisältää kaikki funktion f potentiaaliset arvot.p(f^*|x^*, f) = Tämä on odotettujen funktioarvojen f ehdollinen todennäköisyysjakauma*klo x*, koska funktioarvot f joissakin välipaikoissa.p(f|y,x) = Tämä on funktioarvojen (f) ehdollinen todennäköisyysjakauma, kun otetaan huomioon havaitut tiedot (y) ja niiden syöttöpaikat (x).
Tehtävissä, kuten epävarmuustietoisessa päätöksenteossa ja aktiivisessa oppimisessa, tämä jakauma tarjoaa ennusteen epävarmuuden mittarin, josta voi olla apua.
Gaussin prosessin regression vaiheet
- Tiedonkeruu : Kerää regressio-ongelmasi syöte-lähtö-dataparit.
- Valitse ydinfunktio : Valitse ongelmaasi sopiva kovarianssifunktio (ydin). Ytimen valinta vaikuttaa niiden funktioiden muotoon, joita GPR voi mallintaa.
- Parametrien optimointi : Arvioi ytimen funktion hyperparametrit maksimoimalla tietojen todennäköisyys. Tämä voidaan tehdä käyttämällä optimointitekniikoita, kuten gradienttilaskua.
- Ennustus: Kun olet saanut uuden syötteen, käytä koulutettua GPR-mallia ennustamiseen. GPR tarjoaa sekä ennustetun keskiarvon että siihen liittyvän epävarmuuden (varianssin).
Gaussin prosessiregression (GPR) toteutus
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Lähtö:
Luo tässä koodissa ensin joitakin näytedatapisteitä, joihin on lisätty kohinaa, määritä sitten RBF-ydin ja luo a Gaussin prosessin regressori sen kanssa. Mallia opetetaan harjoitustietojen perusteella ja sitä käytetään testidatan ennusteiden tekemiseen. Lopuksi tulokset visualisoidaan kaaviolla, joka näyttää harjoitustiedot, ennustetun keskiarvon ja 95 %:n luottamusvälin.
Gaussin prosessin toteutus Pythonissa
Scikit Opi
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Pythonin Gaussian Process Regression (GPR) -kirjastot tuodaan tällä koodilla. nämä ovat SciPy lineaarisille algebrafunktioille, NumPy numeerisia operaatioita varten ja Matplotlib tietojen visualisointia varten. Varmistaakseen, että se on yhteensopiva tarvittavien pakettien kanssa, se tarkistaa lisäksi Python-version ja tulostaa sen sekä NumPy- ja scikit-learn-versiot (sklearn).
Ytimen valinta
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Lähtö:
java-piste
[RBF(length_scale=1),
RationalQuadratic(alfa=1, pituusaste=1),
ExpSineSquared(length_scale=1, periodicity=10),
PisteTuote(sigma_0=1)** 2,
Äiti(pituusmittakaava=1, nu=1,5)]
Koodi määrittää testipaikkojen lukumäärän (n) ja alustaa a satunnainen siemen . Valittujen ytimien näyttämiseksi se luo luettelon useista ytimen funktioista ja tulostaa luettelon.
Ytimen vertailu ja visualisointi
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Lähtö:
RBF
gp.kernel_ RBF(length_scale=1,93)
gp.log_marginal_likelihood: -3,444937833462133
--------------------------------------------------- -
Rational Quadratic

gp.kernel_ RationalQuadratic(alpha=1e+05, pituusmittakaava=1,93)
gp.log_marginal_likelihood: -3,4449718909150966
---------------------------------------------------
ExpSineSquared

nopea lajittelu java
gp.kernel_ ExpSineSquared(length_scale=0.000524, periodicity=2.31e+04)
gp.log_marginal_likelihood: -3,4449381454930217
---------------------------------------------------
Pistetuote

gp.kernel_ DotProduct(sigma_0=0,998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
---------------------------------------------------
Äidin

gp.kernel_ Matern(length_scale=1.99, nu=1.5)
gp.log_marginal_likelihood: -5.131637070524745
---------------------------------------------------
Koodi alkaa kiertämällä kernel_-luettelossa lueteltuja ytimen funktioita. Gaussian Process Regressor (gp) tehdään käyttämällä tiettyä ydintä jokaiselle ytimelle. Gaussin prosessille tämä määrittää kovarianssirakenteen. Edellisen jakauman arvioimiseksi muodostetaan joukko testitulopisteitä nimeltä x_test, joiden arvot vaihtelevat -5:stä 5:een. Tämä pistejoukko muunnetaan sarakevektoriksi.
npm välimuisti tyhjennetty
gp.predict-menetelmää käyttäen aiemman jakauman keskiarvo (mu_prior) ja keskihajonta (sd_prior) määritetään kussakin testipisteessä. Keskihajonnan arvoja pyydetään return_std=True-vaihtoehdolla. gp.sample_y (x_test, 3) käytetään kolmen funktion näytteen saamiseksi edellisestä jakaumasta.
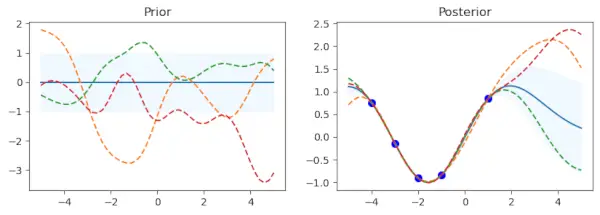
Ensimmäinen osakuvaaja näyttää edellisen jakauman keskiarvon, ja keskihajonnan edustaa varjostettu alue. Näytteet on asetettu päällekkäin katkoviivoina, kun taas keskiarvo näytetään yhtenäisenä viivana. Siellä on osajuoni nimeltä Prior. Niissä on määritetty joukko harjoitustietopisteitä (x_train) ja tavoitearvoja (y_train). Gaussin prosessin malli sovitetaan käyttämällä näitä pisteitä (gp.fit(x_train, y_train)). Viisi datapistettä vastaavilla siniarvoilla muodostavat harjoitustiedot tässä koodissa.
Harjoitteludatan sovitusvaiheen jälkeen menettely laskee posteriorisen jakauman keskiarvon (mu_post) ja keskihajonnan (sd_post) samoille testipisteille (x_test). gp.sample_y(x_test, 3) käytetään myös tuottamaan funktionäytteitä posteriorista jakaumasta. Toinen alikaavio peittää näytteistetyt funktiot katkoviivoina ja näyttää takajakauman keskiarvon, varjostettuna keskihajonnan kanssa. Harjoituksen datapisteet on merkitty sinisellä. Alajuonen nimi on Posterior.
Jos haluat nähdä nykyisen ytimen edelliset ja jälkeiset kaaviot ja saada visuaalisen käsityksen mallin toiminnasta, kutsu Matplotlibin plt.show()-funktio.
Koodi näyttää tiedot nykyisestä ytimestä, kuten gp.kernel_, joka osoittaa nykyisen ytimen, ja gp.log_marginal_likelihood (gp.kernel_.theta), joka antaa nykyistä ydintä käyttävän mallin logarin marginaalitodennäköisyyden jokaisen aikaisemman ja jälkeisen kaaviosarjan jälkeen.
Gaussin prosessiregression (GPR) edut
Gaussin prosessiregressiolla (GPR) on useita etuja useissa sovelluksissa:
- GPR tarjoaa todennäköisyyspohjaisen viitekehyksen regressiolle, mikä tarkoittaa, että se antaa pisteestimaattien lisäksi myös epävarmuusestimaatteja ennusteille.
- Se on erittäin joustava ja voi siepata monimutkaisia suhteita tiedoissa.
- GPR voidaan sovittaa erilaisiin sovelluksiin, mukaan lukien aikasarjaennuste, optimointi ja Bayesin optimointi.
Gaussin prosessiregression (GPR) haasteet
- GPR voi olla laskennallisesti kallista käsiteltäessä suuria tietojoukkoja, koska vaaditaan kovarianssimatriisin inversio.
- Ytimen funktion ja sen hyperparametrien valinta voi vaikuttaa merkittävästi mallin suorituskykyyn.
Hyviä esimerkkejä GPR-sovelluksista
- Osakkeen hinnan ennuste: GPR:llä voidaan mallintaa ja ennustaa osakekursseja ottaen huomioon rahoitusmarkkinoiden volatiliteetti ja epävarmuus.
- Tietokonekokeet: GPR on hyödyllinen optimoitaessa monimutkaisia simulaatioita mallintamalla tulo-lähtösuhteita ja tunnistamalla vaikutusvaltaisimmat parametrit.
- Anomalian tunnistus: GPR:ää voidaan soveltaa poikkeamien havaitsemiseen, jossa se tunnistaa aikasarjatiedon epätavalliset kuviot sieppaamalla normaalit datajakaumat.
Johtopäätös
Yhteenvetona voidaan todeta, että Gaussin prosessiregressio on arvokas työkalu tietojen analysointiin ja ennustamiseen tilanteissa, joissa ennusteiden epävarmuuden ymmärtäminen on välttämätöntä. Hyödyntämällä todennäköisyysmallinnusta ja ytimen toimintoja, GPR voi tarjota tarkkoja ja tulkittavia tuloksia. Laskennalliset kustannukset ja asiantuntijapanoksen tarve on kuitenkin ratkaisevan tärkeää ottaa huomioon GPR:n käytännössä.
