The Harmaa koodi on binäärilukujärjestelmien sarja, joka tunnetaan myös nimellä heijastuva binäärikoodi . Syy tämän koodin kutsumiseen heijastuneena binäärikoodina on ensimmäiset N/2-arvot verrattuna viimeisten N/2-arvojen arvoihin käänteisessä järjestyksessä. Tässä koodissa kaksi peräkkäistä arvoa eroavat toisistaan yhdellä binäärinumeron bitillä. Harmaita koodeja käytetään yleisessä laitteistolla luotujen binäärilukujen sarjassa. Nämä luvut aiheuttavat epäselvyyksiä tai virheitä, kun yhdestä numerosta peräkkäiseen siirrytään. Tämä koodi yksinkertaisesti ratkaisee tämän ongelman muuttamalla vain yhtä bittiä, kun siirtyminen numeroiden välillä on tehty.
Harmaa koodi on erittäin kevyt painotettu koodi, koska se ei riipu paikan määrittämän numeron arvosta. Tätä koodia kutsutaan myös sykliseksi muuttujakoodiksi, koska yhden arvon siirtyminen sen peräkkäiseen arvoon sisältää vain yhden bitin muutoksen.
Kuinka luoda harmaakoodi?
Etuliite- ja heijastusmenetelmää käytetään rekursiivisesti luomaan numeron harmaakoodi. Harmaan koodin luominen:
- Löydämme luvun esittämiseen tarvittavien bittien määrän.
- Seuraavaksi löydämme koodin 0:lle eli 0000:lle, joka on sama kuin binääri.
- Otetaan nyt edellinen koodi, eli 0000, ja muutetaan sen merkittävintä bittiä.
- Suoritamme tämän prosessin yksinomaisesti, kunnes kaikkia koodeja ei tunnisteta yksiselitteisesti.
- Jos merkitsevintä bittiä muuttamalla löydämme saman aiemmin saadun koodin, niin toiseksi merkitsevin bitti muutetaan ja niin edelleen.
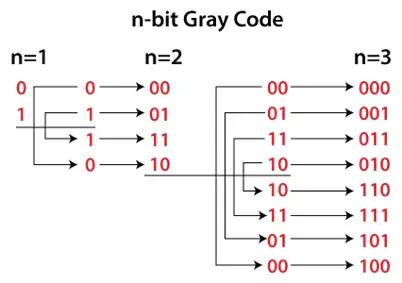
Gray Coden luontiprosessi

Harmaa kooditaulukko
| Desimaaliluku | Binääriluku | Harmaa koodi |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| yksitoista | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| viisitoista | 1111 | 1000 |
