Ahne menetelmä on yksi strategioista, kuten hajota ja hallitse, joita käytetään ongelmien ratkaisemiseen. Tätä menetelmää käytetään optimointiongelmien ratkaisemiseen. Optimointiongelma on ongelma, joka vaatii joko maksimi- tai minimituloksia. Ymmärretäänpä muutamien termien kautta.

Greedy-menetelmä on yksinkertaisin ja yksinkertaisin lähestymistapa. Se ei ole algoritmi, vaan se on tekniikka. Tämän lähestymistavan päätehtävä on, että päätös tehdään tällä hetkellä saatavilla olevan tiedon perusteella. Riippumatta nykyisestä tiedosta, päätös tehdään ilman huolta nykyisen päätöksen vaikutuksista tulevaisuudessa.

ero illallisen ja illallisen välillä

Tätä tekniikkaa käytetään periaatteessa sen toteuttamiskelpoisen ratkaisun määrittämiseen, joka voi olla tai ei ole optimaalinen. Toteutettava ratkaisu on osajoukko, joka täyttää annetut kriteerit. Optimaalinen ratkaisu on ratkaisu, joka on osajoukon paras ja edullisin ratkaisu. Toteutettavuuden tapauksessa, jos useampi kuin yksi ratkaisu täyttää annetut kriteerit, niitä pidetään toteuttamiskelpoisina, kun taas optimaalinen ratkaisu on paras ratkaisu kaikista ratkaisuista.

Greedy-menetelmän ominaisuudet

Seuraavat ovat ahneelle menetelmälle ominaisia ​​piirteitä:

• Ratkaisun muodostamiseksi optimaalisella tavalla tämä algoritmi luo kaksi joukkoa, joista yksi sisältää kaikki valitut kohteet ja toinen joukko hylätyt kohteet.
• Greedy-algoritmi tekee hyviä paikallisia valintoja siinä toivossa, että ratkaisun tulisi olla joko toteuttamiskelpoinen tai optimaalinen.

Greedy Algorithmin osat

Komponentit, joita voidaan käyttää ahneessa algoritmissa, ovat:

jos muuten silmukka javassa

Ehdokassarja:Joukosta luotu ratkaisu tunnetaan ehdokasjoukona.Valintatoiminto:Tällä funktiolla valitaan ehdokas tai osajoukko, joka voidaan lisätä ratkaisuun.Toteutettavuustoiminto:Funktio, jota käytetään määrittämään, voidaanko ehdokasta tai osajoukkoa käyttää osallistumaan ratkaisuun vai ei.Objektiivinen toiminto:Toimintoa käytetään antamaan arvo ratkaisulle tai osaratkaisulle.Ratkaisutoiminto:Tätä toimintoa käytetään selvittämään, onko täydellinen toiminto saavutettu vai ei.

Greedy-algoritmin sovellukset

• Sitä käytetään lyhimmän polun löytämiseen.
• Sitä käytetään minimivirittävän puun etsimiseen primin tai Kruskal-algoritmin avulla.
• Sitä käytetään työjärjestyksissä, joissa on määräaika.
• Tätä algoritmia käytetään myös murto-osien reppuongelman ratkaisemiseen.

Greedy Algorithmin pseudokoodi

 Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } 

Yllä oleva on ahne algoritmi. Aluksi ratkaisulle annetaan arvo nolla. Välitämme taulukon ja elementtien lukumäärän ahneessa algoritmissa. For-silmukan sisällä valitsemme elementin yksitellen ja tarkistamme, onko ratkaisu toteutettavissa vai ei. Jos ratkaisu on toteuttamiskelpoinen, toteutamme liiton.

Ymmärretään esimerkin kautta.

Oletetaan, että on ongelma 'P'. Haluan matkustaa paikasta A paikkaan B seuraavasti:

P: A → B

Ongelmana on, että meidän täytyy matkustaa tämä matka paikasta A paikkaan B. On olemassa erilaisia ​​​​ratkaisuja mennä paikasta A paikkaan B. Voimme mennä paikasta A paikkaan B kävely, auto, pyörä, juna, lentokone jne. Matkalla on rajoitus, jonka mukaan meidän on kuljettava tämä matka 12 tunnin sisällä. Jos menen junalla tai lentokoneella, voin kattaa tämän matkan 12 tunnissa. Tähän ongelmaan on monia ratkaisuja, mutta vain kaksi ratkaisua täyttää rajoituksen.

Jos sanomme, että meidän on katettava matka minimikustannuksin. Tämä tarkoittaa, että meidän on kuljettava tämä matka mahdollisimman vähän, joten tämä ongelma tunnetaan minimointiongelmana. Toistaiseksi meillä on kaksi toteuttamiskelpoista ratkaisua, eli yksi junalla ja toinen lentoteitse. Koska junalla matkustaminen johtaa mahdollisimman pieniin kustannuksiin, se on optimaalinen ratkaisu. Optimaalinen ratkaisu on myös toteuttamiskelpoinen ratkaisu, mutta parhaan tuloksen tarjoava ratkaisu on optimaalinen ratkaisu pienin kustannuksin. Olisi vain yksi optimaalinen ratkaisu.

Ongelma, joka vaatii joko minimi- tai maksimituloksen, tunnetaan optimointiongelmana. Ahne menetelmä on yksi strategioista, joita käytetään optimointiongelmien ratkaisemiseen.

python-ohjelmat

Greedy-algoritmin käytön haitat

Ahne algoritmi tekee päätökset jokaisessa vaiheessa saatavilla olevan tiedon perusteella ottamatta huomioon laajempaa ongelmaa. Joten voi olla mahdollista, että ahne ratkaisu ei anna parasta ratkaisua jokaiseen ongelmaan.

Se seuraa paikallista optimivalintaa kussakin vaiheessa tavoitteenaan löytää globaali optimi. Ymmärretään esimerkin kautta.

yritä saada java kiinni

Harkitse alla olevaa kaaviota:

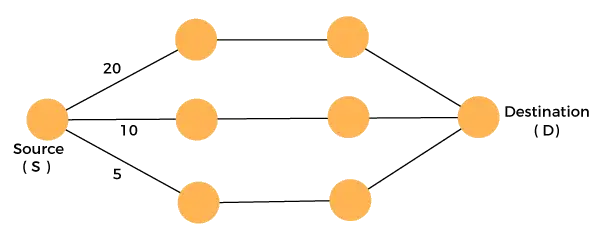
Meidän täytyy matkustaa lähteestä määränpäähän pienin kustannuksin. Koska meillä on kolme toteuttamiskelpoista ratkaisua, joiden kustannuspolut ovat 10, 20 ja 5, 5 on pienin kustannuspolku, joten se on optimaalinen ratkaisu. Tämä on paikallinen optimi, ja tällä tavalla löydämme paikallisen optimin jokaisessa vaiheessa globaalin optimaalisen ratkaisun laskemiseksi.