Esittely:

Puolisummain on digitaalinen logiikkapiiri, joka suorittaa kahden yksibittisen binaariluvun binäärilisäyksen. Siinä on kaksi tuloa, A ja B, ja kaksi lähtöä, SUM ja CARRY. SUM-lähtö on tuloksen vähiten merkitsevä bitti (LSB), kun taas CARRY-lähtö on tuloksen merkittävin bitti (MSB), joka osoittaa, onko kahden tulon lisäämisestä aiheutunut siirtoa. Puolisummain voidaan toteuttaa käyttämällä perusportteja, kuten XOR- ja AND-portteja.

Toki tässä on syvällisempi selitys puolisummainpiiristä:

Puolisummain on perusrakennuspalikka monimutkaisemmille summainpiireille, kuten täyssummaimille ja monibitisille summaimille. Se suorittaa kahden yksibittisen tulon A ja B binaarilisäyksen ja tarjoaa kaksi lähtöä, SUM ja CARRY.

SUM-lähtö on tuloksen vähiten merkitsevä bitti (LSB), joka on kahden tulon A ja B XOR. XOR-portti toteuttaa binäärinumeroiden yhteenlaskuoperaation, jossa SUM-lähtöön generoidaan 1 vain, kun yksi tuloista on 1.

CARRY-lähtö on tuloksen merkittävin bitti (MSB), joka osoittaa, onko kahden tulon lisäämisestä tapahtunut siirtoa. CARRY-lähtö on AND kahdesta tulosta A ja B. AND-portti luo 1:n CARRY-lähtöön vain, kun molemmat tulot ovat 1.

Half Adder (HA):

Puolisummain on yksinkertaisin summainpiireistä. Puolisummain on yhdistelmäaritmeettinen piiri, joka summaa kaksi numeroa ja tuottaa sekä summabitin (s) että siirtobitin (c) ulostulona. 2 bitin lisääminen tehdään käyttämällä yhdistelmäpiiriä, jota kutsutaan puolisummaimeksi. Syöttömuuttujat ovat augend- ja addend-bittejä ja lähtömuuttujat ovat summa & carry -bittejä. A ja B ovat kaksi tulobittiä.

Tarkastellaan kahta tulobittiä A ja B, jolloin summabitti (s) on A:n ja B:n X-OR. puolisummaimen funktiosta käy ilmi, että se vaatii yhden X-TAI-portin ja yhden AND-portin. rakentaminen.

Totuustaulukko:

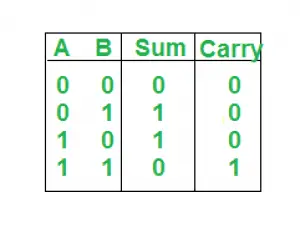
Tässä suoritetaan kaksi operaatiota Sum ja Carry, joten tarvitsemme kaksi K-mapsia, yksi kummallekin lausekkeen johtamiseksi.

Looginen lauseke:

Summa:

Summa = A XOR B

hashset java

Kantamiseen:

Kanto = A JA B

Toteutus:

Huomautus: Puolisummaimella on vain kaksi sisääntuloa, eikä alemman kertaluvun biteistä tulevaa siirtoa ole mahdollista lisätä, kun suoritetaan usean lisäyksen.

Half Adderin edut ja haitat digitaalisessa logiikassa:

Half Adderin edut digitaalisessa logiikassa:

1. Yksinkertaisuus: Puoliviper on suoraviivainen piiri, joka vaatii pari perusosaa, kuten XOR JA sisäänkäynti. Se ei ole vaikea toteuttaa ja sitä voidaan käyttää useissa edistyneissä kehyksissä.

2. Nopeus: Puoliviper toimii erittäin nopeasti, mikä tekee siitä kohtuullisen käytettävän nopeissa tietokonepiireissä.

Half Adderin haitat digitaalisessa logiikassa:

1. Rajoitettu käyttökelpoisuus: Puolikas kyy voi lisätä kaksi yksiosaista numeroa ja tuottaa kokonais- ja välitysbitin. Se ei voi suorittaa monibittisten lukujen laajentamista, mikä edellyttää monimutkaisten lisäpiirien, kuten täyden summaimen, käyttöä.

2. Välittämistietojen puute: Puolikäärmeellä ei ole välityssyöttöä, mikä rajoittaa sen arvoa hämmästyttävämmissä laajennustehtävissä. Välityssyöte on tärkeä monibittisten lukujen laajentamiseksi ja useiden summainten ketjuttamiseksi yhteen.

3. Levityksen lykkäys: Puolikäärmepiirissä on leviämisviive, joka on aika, joka kuluu tuloksen muuttumiseen tiedon säätämisen valossa. Tämä voi aiheuttaa ajoitusongelmia tietokonepiireissä, erityisesti nopeissa kehyksissä.

Half Adderin käyttö digitaalisessa logiikassa:

1. Aritmeettiset piirit: Puolisummaimia käytetään numeronmurskauspiireissä kaksoislukujen lisäämiseen. Siinä vaiheessa, kun eri puolisummaimia liittyy ketjuun, ne voivat lisätä monibittisiä kaksoislukuja.

2. Tietojen käsittely: Puolisummaimia käytetään tiedonkäsittelysovelluksissa, kuten tietokoneistettu signaalinkäsittely, tiedon salaus ja virhesäätö.

3. Osoitteen purkaminen: Muistiin pyrkivässä puolisummaimia käytetään osoitteiden salauspiireissä tietyn muistialueen sijainnin tuottamiseksi.

4. Enkooderi- ja dekooderipiirit: Puolisummaimia käytetään kooderi- ja dekooderipiireissä tietokoneistettuihin vastaavuuskehyksiin.

5. Multiplekserit ja demultiplekserit: Puolisummaimia käytetään multipleksereissä ja demultipleksereissä kurssitietojen valitsemiseen.

6. Laskurit: Puolisummaimia käytetään laskureissa lisäämään lukemaa yhdellä.

satunnainen c