Kulma mitataan asteina (°) ja radiaaneina. Se muodostuu monikulmion kahden vierekkäisen sivun väliin. Jokaisella polygonilla on eri sivut ja eri määrä kulmia. Kaava kulmien löytämiseksi asteina on hyödyllinen geometriassa ja trigonometriassa. On välttämätöntä ymmärtää muita matematiikan käsitteitä, kuten kaari, ympyrän keskikulma jne.

1. Täysi ympyrä = 360°
2. Suora = 180°
3. Puoliympyrä = 180°
4. A Neljännesympyrä = 90°

Kulmien laskeminen asteina

On olemassa kolme erilaista tapaa löytää kulmat asteina, jotka ovat seuraavat:

1. Suojan käyttö D
2. Pythagoras-lauseen ja trigonometriafunktion käyttäminen suorakulmaisessa kolmiossa
3. Kulmien summakaavan käyttäminen
4. Ympyrän keskikulma

Suojan käyttö D

Suoja on eräänlainen viivain tai asteikko, jota käytetään mittaamaan etäisyyttä senttimetreinä tai millimetreinä. Kulmien mittaamiseen käytetty suojus on 'D':n muotoinen, ja kulmien arvot on merkitty 0 - 180° kummasta tahansa suunnasta (oikealle tai vasemmalle). Meidän on kohdistettava akseli D-viivan kanssa kulman mittaamiseksi. Suojan keskiympyrä on kohdistettu mitattavan kulman kärjen kanssa. Kulman kärkeä pitkin kulkevat säteet auttavat löytämään kulman asteina.

Pythagoras-lauseen ja trigonometriafunktion käyttäminen suorakulmaisessa kolmiossa

Trigonometriassa on kuusi funktiota, sini, cos, cosec, tan, pinnasänky, ja sek. Suorakulmaisella kolmiolla on kolme sivua, kanta, kohtisuora ja hypotenuusa.

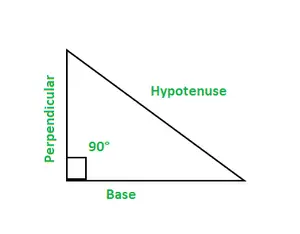
Pohja: Se on 90° kulman viereinen sivu. Kohtisuora: Se on myös 90° kulman viereinen sivu. Hypotenuusa: Se on 90° kulman vastainen sivu.

Suorakulmaista kolmiota edustaa 90°:n kulma yhtenä kulmista. Kolmion kulmien kokonaissumma on 180°.

Cosecθ: Se esitetään hypotenuusana jaettuna kohtisuoralla.

Cosecθ =

Cotθ: Se esitetään kantana jaettuna kohtisuoralla.

Cotθ =

Muut trigonometriset funktiot esitetään seuraavasti:

sinθ =

Cosθ =

tanθ =

secθ =

Cosecθ voidaan esittää myös muodossa 1/sinθ

secθ voidaan esittää myös muodossa 1/cosθ

Cotθ voidaan esittää myös muodossa 1/tanθ

Missä,

Θ on kulma

Pythagoraan lause

Jos tunnetaan suoran kulman kaksi sivua, voimme helposti laskea suorakulmaisen kolmion kolmannen sivun. Suorakulmaisessa kolmiossa Pythagoras-lause on annettu seuraavasti:

(Hypotenuusa)²= (Perus)²+ (pystysuorassa)²

Kulmien summan kaava

Kulmien summa tarkoittaa monikulmion sisäisten kulmien kokonaissummaa, joka muodostuu kahden sivun väliin. Jos monikulmion sivuja on kuusi, kulmaa on noin kuusi. Kulman löytäminen auttaa, jos muut kulmat ja monikulmion kulmien summa tunnetaan.

Kaava monikulmion kulmien kokonaissumman löytämiseksi saadaan seuraavasta:

Kulmien kokonaissumma = 180 (n – 2)

Missä,

n on monikulmion sivujen lukumäärä

Esimerkki:

• Jos n = 4,

Kulmien kokonaissumma = 180 (4–2)

= 180 (2)

= 360°

Jos n = 5,

Kulmien kokonaissumma = 180 (5–2)

= 180 (3)

= 540°

• Jos n = 6

Kulmien kokonaissumma = 180 (6–2)

= 180 (4)

= 720°

Ympyrän keskikulma

Ympyrä on pyöreä muoto, jonka raja on yhtä kaukana sen keskipisteestä. Keskipisteen ja rajan välinen etäisyys tunnetaan ympyrän säteenä. Ympyrän kahden säteen muodostama kulma tunnetaan keskikulmana. Ympyrän keskikulman arvo on välillä 0 - 360 astetta.

Kaava ympyrän keskikulman laskemiseksi saadaan seuraavasta:

Kaaren pituus = 2πr × (θ/360)

Θ = 360L/2pr

Missä,

r on ympyrän säde

AB on kaari

Theta on kulma asteina.

L = Kaaren pituus

Esimerkkiongelmat

Kysymys 1: Löydä keskikulma ympyrälle, jonka säde on 2 m ja kaaren pituus 4 m?

Ratkaisu :

Kaava ympyrän keskikulman laskemiseksi saadaan seuraavasta:

Θ = 360L/2pr

Missä,

r on ympyrän säde

Theta on kulma asteina.

L = Kaaren pituus

Θ = Kulma asteina

r = 2m

L = 4 m

Θ = 360 × 4 /2 × π × 2

Θ = 114,6°

Siten ympyrän keskikulma on 114,6°.

Kysymys 2: Löydä keskikulma ympyrälle, jonka säde on 10 cm ja kaaren pituus 18 cm?

Ratkaisu :

Kaava ympyrän keskikulman laskemiseksi saadaan seuraavasta:

Θ = 360L/2pr

Missä,

r on ympyrän säde

Theta on kulma asteina.

L = Kaaren pituus

r = 10 cm

L = 18 cm

Θ = Kulma asteina

Θ = 360 × 18 /2 × π × 10

Θ = 103,13°

Siten ympyrän keskikulma on 103,13°.

Kysymys 3: Etsi suunnikkaan kulma, jos muut kolme kulmaa ovat 80°, 95° ja 105°?

Ratkaisu :

Suunnikkaassa on neljä sivua, joiden kulmien kokonaissumma on 360°.

merkkijono vertaa javaa

Kaava kulmien summan löytämiseksi = 180 (n – 2)

Missä,

n on monikulmion sivujen lukumäärä

Tässä n = 4,

Kulmien kokonaissumma = 180 (4-2)

uri vs url

= 180 (2)

= 360°

Kokonaissumma = kulma 1 + kulma 2 + kulma 3 + kulma 4

360 = 80+ 95+ 105+ Kulma 4

360 = 280 + Kulma 4

Kulma 4 = 360–280

Kulma 4 = 80°

Kysymys 4: Etsi kulma A annetusta kuvasta.

Ratkaisu :

Annettu: Hypotenuusa = 12

kohtisuora = 6

Trigonometriafunktio kulman laskemiseksi saadaan seuraavasti:

sinA = 6/12

A = 30°

Kysymys 5: Etsi kulma A annetusta kuvasta.

Ratkaisu :

Annettu: Hypotenuusa = 10

Pohja = 5

Trigonometriafunktio kulman laskemiseksi saadaan seuraavasti:

CosA = 5/10

A = 60°

Kysymys 6: Etsi viisikulmion kulma, jos muut neljä kulmaa ovat 115°, 100°, 105° ja 100°?

Ratkaisu :

Viisikulmiossa on viisi sivua, joiden kulmien yhteissumma on 540°.

Kaava kulmien summan löytämiseksi = 180 (n – 2)

Missä,

n on monikulmion sivujen lukumäärä

Tässä n = 5,

Kulmien kokonaissumma = 180 (5–2)

= 180 (3)

= 540°

Kokonaissumma = kulma 1 + kulma 2 + kulma 3 + kulma 4 + kulma 5

540 = 115° + 100° + 105° + 100° + kulma 5

540 = 420 + Kulma 5

Kulma 5 = 540–420

Kulma 5 = 120°

Kysymys 7: Etsi kulma A annetusta kuvasta.

Ratkaisu :

Annettu: kanta = √3

kohtisuora = 1

Trigonometriafunktio kulman laskemiseksi saadaan seuraavasti:

tanθ =

tanθ = 1/√3

A = 30°

Kysymys 8: Etsi suunnikkaan kulma, jos muut kolme kulmaa ovat 100°, 70° ja 80°?

Ratkaisu :

Suunnikkaassa on neljä sivua, joiden kulmien kokonaissumma on 360°.

Kaava kulmien summan löytämiseksi = 180 (n – 2)

Missä,

n on monikulmion sivujen lukumäärä

Tässä n = 4,

Kulmien kokonaissumma = 180 (4–2)

= 180 (2)

= 360°

Kokonaissumma = kulma 1 + kulma 2 + kulma 3 + kulma 4

360 = 100 + 70 + 80 + Kulma 4

360 = 250 + Kulma 4

Kulma 4 = 360–250

Kulma 4 = 110°

Siten toinen kulma on 110°.

Kysymys 9: Etsi kuusikulmion kulma, jos muut viisi kulmaa ovat 120°, 115°, 110°, 125° ja 105°?

Ratkaisu :

Kuusikulmiossa on kuusi sivua, joiden kulmien kokonaissumma on 720°.

Kaava kulmien summan löytämiseksi = 180 (6 – 2)

Missä,

n on monikulmion sivujen lukumäärä

Tässä n = 6,

Kulmien kokonaissumma = 180 (6–2)

= 180 (4)

= 720°

Kokonaissumma = kulma 1 + kulma 2 + kulma 3 + kulma 4 + kulma 5 + kulma 6

720 = 120 + 115 + 110 + 125 + 105 + kulma 6

720 = 575 + Kulma 6

Kulma 6 = 720–575

Kulma 6 = 145°

Siten kuusikulmion kuudes kulma on 145°.