Kolmiot ovat kolmisivuisia suljettuja polygoneja, jotka muodostuvat kolmen suoran leikkauspisteestä. Sitä kohtaa paljon jokapäiväisessä elämässä. Se on yksi geometrian perusmuodoista. Siinä on kolme sivua, kolme kulmaa ja kolme kärkeä. Suorakulmainen kolmio on sellainen, jossa yksi kulmista on aina yhtä suuri kuin 90°. Pythagoraan lause on johdettu suorakulmaisille kolmioille, joka kertoo, että hypotenuusan neliö (pisin sivu) on yhtä suuri kuin kanta- ja kohtisuoran neliöiden summa.

Kun otetaan huomioon suorakulmaisen kolmion vähintään kahden sivun pituus, voimme löytää suorakulmaisen kolmion minkä tahansa kulman arvon. Tätä varten käytämme erilaisia ​​trigonometrisiä funktioita, kuten sini, kosini, tangentti, kotangentti, sek ja kosek. Nämä auttavat meitä suhteuttamaan suorakulmaisen kolmion kulmat sen sivuihin.

Ominaisuudet

• Kolmen kärjen joukossa on suorakulmainen kärki
• Suorakulmaisen kärjen vastakkaista puolta kutsutaan nimellä hypotenuusa .
• Sivujen pituus noudattaa Pythagoras-lausetta, jonka mukaan

hypotenuusa ² = pohja ² + korkeus ²

• Hypotenuusa on suorakulmaisen kolmion pisin sivu.
• Muut kulmat kuin suora kulma ovat teräviä kulmia, koska arvo on pienempi kuin 90^O

Trigonometriset funktiot

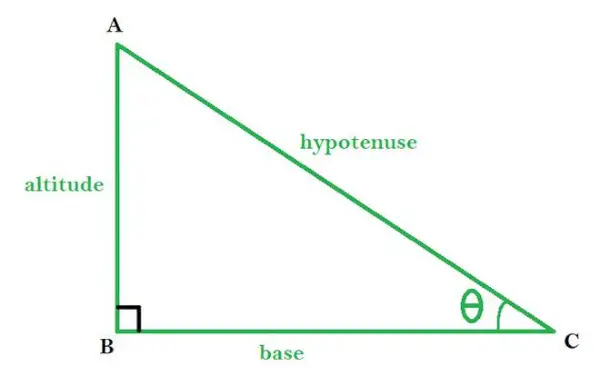
ABC on suorakulmainen kolmio, jossa ∠B on suorakulmainen

ota kiinni ja kokeile javaa

• cosθ: Tämä antaa kannan suhteen suorakulmaisen kolmion hypotenuusan mukaan.

cosθ = kanta / hypotenuusa

• sinθ: Tämä antaa korkeuden suhteen suorakulmaisen kolmion hypotenuusan mukaan.

sinθ = korkeus / hypotenuusa

• tanθ: Se on korkeuden suhde suorakulmaisen kolmion kantaan.

tanθ = korkeus / tukikohta

• cotθ: Se on tanθ:n käänteisarvo
• sekθ: Se on cosθ:n käänteisarvo
• cosecθ: Se on sinθ:n käänteiskohta

Suorakulmaisen kolmion kulmien löytämiseksi voimme ottaa trigonometrisen käänteisen kolmion annettujen sivujen suhteen.

Esimerkki:

Jos sinθ = x, voimme kirjoittaa

θ = synti ^-1 x.

Tämä palauttaa kulman, jonka kulman siniarvo on x.

Samoin on olemassa cos^-1θ, niin^-1minä, pinnasänky^-1θ, sek^-1θ ja kosek^-1i

Esimerkkiongelmat

Kysymys 1. Annettu suorakulmainen kolmio, jonka kanta on 10 cm ja hypotenuusa 20 cm. Etsi peruskulman arvo.

Ratkaisu:

Annettu pohja = 10 cm

Hypotenuusa = 20 cm

Olkoon kantakulman arvo θ. Voimme kirjoittaa

cosθ = kanta / hypotenuusa = 10/20 = 1/2

θ = cos^-1(1/2) = 60^O

Siten peruskulman arvo on 60 ^O .

Tehtävä 2. Laske suorakulmaisen kolmion kulmien arvo, kun yksi teräväkulmaisista kulmista on kaksi kertaa toinen.

Ratkaisu:

Koska tiedämme, että kolmion kaikkien kolmen kulman summa on 180^O.

Koska yksi kulmista on 90^Oja yksi terävistä kulmista on kaksi kertaa toinen, voimme pitää niitä arvoina θ ja 2θ.

Joten voimme kirjoittaa

90^O+ θ + 2θ = 180^O

3θ = 180^O– 90^O

3θ = 90^O

θ = 90^O/3 = 30 ^O

2θ = 2 × 30^O= 60 ^O

Kulmat ovat siis 30 ^O , 60 ^O , ja 90 ^O .

Kysymys 3. Laske 5 m pitkien tikkaiden korkeuskulman arvo, kun tikkaiden kanta on 3 m etäisyydellä seinästä.

Ratkaisu:

Koska tikkaat toimivat suorakulmaisen kolmion hypotenuusana ja kantaetäisyys on 3 m, voimme kirjoittaa

Hypotenuusa = 5m

Pohja = 3m

Olkoon korkeuskulma θ. Joten voimme kirjoittaa

cosθ = emäs / hypotenuusa = 3/5

θ = cos^-1(3/5)

θ = 53^O

Siten korkeuskulman arvo on 53^O.

Kysymys 4. Laske hypotenuusan arvo, koska korkeuden pituus on 8 m ja kantakulma on 30 ^O .

Ratkaisu:

Tällöin peruskulma on yhtä suuri kuin 30^Oja korkeus on 8 m, voimme käyttää sinifunktiota hypotenuusan pituuden löytämiseksi.

synti30 ^O = korkeus / hypotenuusa

hypotenuusa = korkeus / sin30^O

Koska arvo sin30^Oon yhtä kuin 1/2, voimme kirjoittaa

hypotenuusa = korkeus / (1/2) = 2 × korkeus

Siten hypotenuusa = 2 × 8 = 16 m

Siten hypotenuusan pituus on 16 m.