Kolmion keskipiste on kolmion kaikkien kolmen kulman puolittajan leikkauspiste. Keskipiste on tärkeä piste kolmiossa, jossa viivat, jotka leikkaavat kulmia puoliksi, kohtaavat. Tämä piste on myös Incircle-nimisen ympyrän keskus, joka sopii täydellisesti kolmion sisään ja koskettaa kaikkia kolmea sivua samalla tavalla. Tämä artikkeli käsittelee erilaisia ​​käsitteitä kolmion keskipisteestä, kuten miksi tämä piste on tärkeä, kuinka se löytää kompassin tai numeroiden avulla ja ympyrän keskipisteen ominaisuudet.

Sisällysluettelo

• Mikä on kolmion keskipiste?
• Kolmion incenterin ominaisuudet
• Kolmiokaavan keskipiste
• Kuinka löytää kolmion keskipiste
• Centroid, Circumcenter, Incenter, Orthocenter

Mikä on kolmion keskipiste?

Kolmion keskipiste, kuten nimestä voi päätellä, on kolmion keskipiste. Tämä piste, jota kutsumme keskipisteeksi, muodostuu risteyksestä, jossa kaikki sisäkulmat jakavat suorat kohtaavat. Pisteen etäisyys kolmion kaikista kolmesta sivusta on sama. Kolmion sisäympyrä sopii myös täydelliseen ympyrään kolmion sisälle ja tätä ympyrää kutsutaan kolmion ympyräksi.

Incent määritelmä

Kolmion keskipiste on kolmion sisällä oleva piste, jossa kaikki kolme sen sisäkulmat puoliksi leikkaavaa suoraa kohtaavat. Tämä piste on samalla etäisyydellä kolmion kolmesta sivusta, joten se on kuin kolmion keskikohta. Se on myös suurimman ympyrän keskipiste, joka voi sopia tiukasti kolmion sisään, jota kutsumme ympyräksi. Symboloimaan keskikohtaa käytämme yleensä kirjainta I,

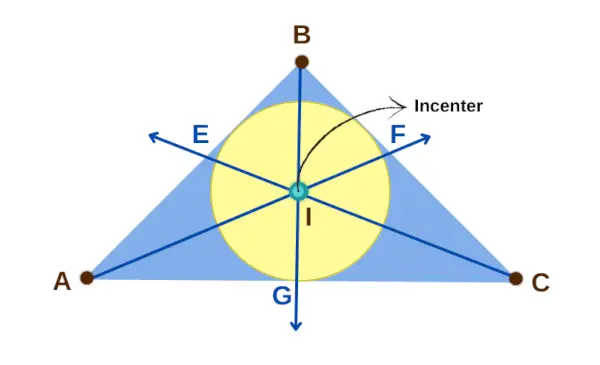
Kolmion keskipiste

Kolmion incenterin ominaisuudet

Alla on joitain tärkeitä kolmion keskikohdan ominaisuuksia:

Omaisuus 1: Jos minä on kolmion ABC keskipiste, silloin kolme janaparia ovat yhtä pitkiä: AE ja AG, CG ja CF sekä BF ja BE. Tämä tarkoittaa, että AE = AG, CG = CF ja BF = BE.

Omaisuus 2: Keskusta minä on myös erityinen suhde kolmion kulmiin. Se saa kulmat ∠BAI ja ∠CAI olemaan yhtä suuret, ∠BCI ja ∠ACI yhtä suuret ja ∠ABI ja ∠CBI yhtä suuret. Tämä seuraa kulman puolittajalausetta.

Omaisuus 3: Keskusta minä on ympyrän keskipiste, joka koskettaa kolmion kaikkia kolmea sivua, ja etäisyydet minä kolmion sivuille (EI, FI, GI) ovat kaikki samat. Näitä etäisyyksiä kutsutaan insäteiksi tai ympyrän säteeksi.

Omaisuus 4: Voit laskea kolmion pinta-alan puolikehän (s) ja säteen (r) avulla. Kaava on A = sr, jossa A on pinta-ala, s on puolikehä (s = (a + b + c)/2, missä a, b ja c ovat kolmion sivujen pituudet) ja r on säde.

Omaisuus 5: Kolmion keskipiste pysyy aina kolmion sisällä. Toisin kuin ortosentti, joka voi joissain tapauksissa olla kolmion ulkopuolella, keskipiste on aina kolmion rajojen sisällä.

Kolmiokaavan keskipiste

Kaava löytääksesi kaavan keskikohdan 3 koordinaatilla (x₁, ja₁), (x₂, ja₂), ja (x₃, ja₃) On:

{(kirves ₁ + bx ₂ + cx ₃ )/(a + b + c), (on ₁ + tekijältä ₂ + c ₃ )/(a + b + c)}

Yksinkertaisesti sanottuna, saadaksesi keskipisteen:

• Kerro pisteen A x-koordinaatti sivun pituudella a, pisteen B x-koordinaatti sivun pituudella b ja pisteen C x-koordinaatti sivun pituudella c. Lisää sitten nämä yhteen.
• Jaa tulos sivujen pituuksien a, b ja c summalla.
• Toista sama prosessi y-koordinaateille, mutta käyttämällä sivun pituuksia a, b ja c.

Kolmiokulmakaavan keskipiste

Kaava kolmion kulman keskipisteen löytämiseksi on seuraava:

Olkoon, Kolmiossa D, F ja G ovat pisteet, joissa kulmien A, B ja C kulman puolittajat kohtaavat sivut BC, AC ja AB.

Kulma ∠AIB (jossa I on kolmion keskipiste) voidaan laskea kaavalla:

∠AIB = 180° – (puolet kulmien A ja B summasta)

TAI

∠AIB = 180° – (∠A + ∠B)/2

Kuinka löytää kolmion keskipiste

On kaksi tapaa löytää kolmion keskipiste. Rakentamisessa paikannamme keskipisteen piirtämällä kolmion kulman puolittajat. Koordinaattigeometriassa käytämme kaavaa keskipisteen määrittämiseen.

Koordinaattigeometrian käyttö : Etsi kolmion keskipiste, jonka koordinaatit ovat: A(2, 2), B(6, 2) ja C(4, 5)

Annettujen tietojen mukaan

• (x₁, ja₁) = (2, 2)
• (x₂, ja₂) = (6, 2)
• (x₃, ja₃) = (4, 5)

Tiedämme, että kolmion keskipiste on:

I(x, y) = {(kirves ₁ + bx ₂ + cx ₃ )/(a + b + c), (on ₁ + tekijältä ₂ + c ₃ )/(a + b + c)}

Sivulle a: Pisteiden B ja C välinen etäisyys = √((6 – 4)²+ (2–5)²) = √8

Sivulle b: Pisteiden A ja C välinen etäisyys = √((2 – 4)²+ (2–5)²) = √13

Sivulle c: Pisteiden A ja B välinen etäisyys = √((6 – 2)²+ (2–2)²) = 4

Laittamalla a, b, c arvot keskipisteen kaavaan, saamme:

I(x, y) = {(8 × 2 + 13 × 5 + 4 × 4)/(8 + 13 +4), (8 × 2 + 13 × 2 + 4 × 5) / (8 + 13 +4 )}

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Kolmion ABC keskipiste koordinaatteineen on (22/5,62/25)

Kuinka rakentaa kolmion keskipiste?

Kolmion keskipisteen muodostaminen edellyttää kompassin käyttöä. Käytä kompassia seuraavasti:

Vaihe 1: Aseta kompassin toinen pää kolmion kärkeen ja toinen pää koskettaa toista sivua.

Vaihe 2: Piirrä kompassin avulla kaksi kaarta kolmion kahdelle sivulle.

Vaihe 3: Tee samalla etäisyydellä kompassista kaksi kaarta kolmion sisään. Näiden kaarien tulee ylittää toistensa kohdasta, jossa ne koskettavat sivuja.

Vaihe 4: Piirrä viiva kolmion kärjestä kahden sisäkaaren risteykseen.

Vaihe 5: Toista samat vaiheet kolmion toisesta kärjestä.

Vaihe 6: Kohta, jossa kaksi viivaa kohtaavat tai leikkaavat, on kolmion keskipiste.

Suorakulmaisen kolmion keskipiste

Keskipiste jos a Suorakulmainen kolmio on piste, jossa kaikki suorakulmaisen kolmion kulman puolittajat kohtaavat. Jos suorakulmaisen kolmion sivujen mitat ovat a, b ja c, niin sisäympyrän säde 'r' annetaan muodossa r = (ab)/(a + b + c). Oikean kolmion keskikohta on kuvattu alla:

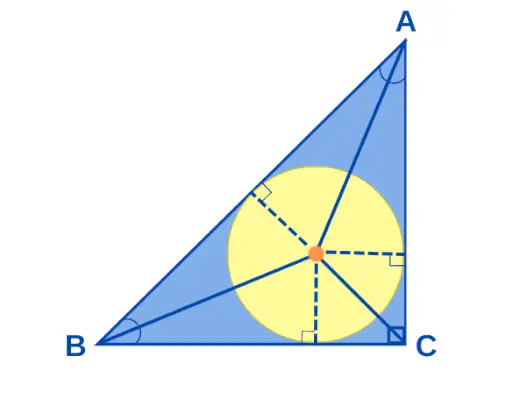
Suorakulmaisen kolmion keskipiste

Centroid, Circumcenter, Incenter, Orthocenter

Centroid, Circumcenter, Incenter ja Orthocenter ovat neljä tärkeää kolmioon liittyvää pistettä. Vertailu Centroidin, Circumcenterin, Incenterin ja Orthocenterin välillä on taulukoitu alla:

python tai

Myös Tarkista

• Kolmion alue
• Kolmion kehä
• Kulman summan ominaisuus kolmion

Esimerkkejä kolmion keskipisteestä

Esimerkki 1: Laske kolmion ABC keskipiste. AB = 8 cm, BC = 15 cm, CA = 17 cm.

Ratkaisu:

Käyttämällä kaavaa kolmion keskipiste = (aA + bB + cC)/(a + b + c)

missä,

• a = 8
• b = 15
• c = 17

Ja kulmat ovat,

• A = 30°
• B = 60°
• C = 90°

Laittamalla nämä arvot kaavaan saadaksesi

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Esimerkki 2: Jane laski kolmion muotoisen kentän pinta-alaksi 120 neliömetriä. Kentän ympärysmitta on 36 metriä. Jos ympyrä piirretään kolmion sisälle siten, että se koskettaa kolmion jokaista sivua, auta Janea laskemaan kolmion säde.

Ratkaisu:

Annettujen tietojen mukaan

Kolmion pinta-ala = 120 neliömetriä

Kolmion ympärysmitta = 36 metriä

Tiedämme, että kolmion pinta-ala = r × s

s = puolikehä

s = p/2 = 36/2 = 18

A = r × s

r = A/s

r = 120/18

r = 6,67 metriä

Harjoittele ongelmia kolmion keskipisteessä

Tehtävä 1: Kun on annettu kolmio PQR, jonka kärjet ovat P(1, 2), Q(4, 6) ja R(7, 2), etsi keskipisteen koordinaatit.

Tehtävä 2: Muodosta kolmio ABC, jossa ∠A = 45°, ∠B = 60° ja ∠C = 75°. Käytä rakennusmenetelmää löytääksesi keskipiste.

Tehtävä 3: Jos kolmiossa LMN ∠L = 75°, ∠M = 60° ja ∠N = 45°, etsi keskipisteen koordinaatit.

Tehtävä 4: Muodosta kolmio XYZ, jossa ∠X = 80°, ∠Y = 50° ja ∠Z = 50°. Käytä rakennusmenetelmää löytääksesi keskipiste.

Kolmion keskipiste: UKK

Mikä on kolmion keskipiste?

Kolmion keskipiste on piste, jossa sisäkulmien puolittajat leikkaavat. Se on yhtä kaukana kolmion kaikista kolmesta sivusta.

Mikä on keskipisteen merkitys kolmiossa?

Keskipiste on merkittävä, koska se on kolmion ympyrän keskipiste, suurin ympyrä, joka sopii kolmion sisään. Sillä on ominaisuus olla yhtä kaukana kaikista puolista.

Voiko incenter olla kolmion ulkopuolella?

Ei, keskipiste on aina kolmion sisällä. Se on kulman puolittajien samanaikaisuuspiste, ja määritelmän mukaan sen on oltava kolmion rajojen sisällä.

Kuinka Incenter muodostetaan käyttämällä kompassia ja suoraa reunaa?

Luodaksesi keskipisteen, piirrä kulman puolittajat kompassin avulla jokaisesta kärjestä vastakkaiselle puolelle. Keskipiste on piste, jossa nämä puolittajat leikkaavat.

Mikä on Incenter Formula?

Kolmion keskipisteen kaava voidaan kirjoittaa seuraavasti:

frac{(aA+bB+cC)}{a+b+c}

Mitkä ovat kolmion keskipisteen ominaisuudet?

Keskuksella on joitain tärkeitä ominaisuuksia. Se on yhtä kaukana kolmion sivuista, mikä tarkoittaa, että etäisyydet sivuihin ovat yhtä suuret. Se on myös kulman puolittajien leikkauspiste, joka jakaa kulmat kahteen yhtä suureen osaan.

Miten keskus määritetään?

Incenterin määrittämiseksi sinun on löydettävä kulman puolittajien leikkauskohta. Tämä voidaan tehdä käyttämällä keskityskaavaa tai piirtämällä kulman puolittajat ja etsimällä niiden leikkauspiste.

Mitä eroa on Incentren ja Circumcentren välillä?

Suurin ero incenterin ja circumcenterin välillä on niiden keskittyminen. Incenter käsittelee kulman puolittajia ja on piirretyn ympyrän keskipiste, kun taas ympyräkeskus käsittelee kohtisuoraa puolittajaa ja on rajatun ympyrän keskipiste.

Onko Incentre ja Centroid sama?

Ei, keskipiste ja painopiste ovat erilaisia. Keskipiste on paikka, jossa kulman puolittajat kohtaavat, kun taas keskipiste on kohta, jossa mediaanit leikkaavat. Mediaanit yhdistävät kärjet vastakkaisen puolen keskipisteeseen.

Onko Incentre ja Orthocentre sama?

Ei, keskipiste ja ortosentti eivät ole sama asia. Incenter on piste, jossa kulma puolittaa toisensa, kun taas ortosentti sisältää korkeudet - viivat jokaisesta kärjestä kohtisuorassa vastakkaiseen sivuun. Ne ovat eri pisteitä kolmiossa.