priority_queue < int, vector , suurempi > minH;>> 
2. Min-Heap Javassa 
Javassa min kaso voidaan toteuttaa käyttämällä    PriorityQueue    luokasta alkaen    java.util-paketti    . PriorityQueue-luokka on prioriteettijono, joka tarjoaa tavan tallentaa elementtejä jonomaiseen tietorakenteeseen, jossa jokaiselle elementille on liitetty prioriteetti.
on yhtä kuin merkkijono javassa
 
    Syntaksi    :
JavaMin-Heap Pythonissa  
Pythonissa min kaso voidaan toteuttaa käyttämällä  kasaq  moduuli, joka tarjoaa toimintoja kasojen toteuttamiseen. Tarkemmin sanottuna    kasaq    moduuli tarjoaa tavan luoda ja käsitellä kasatietorakenteita.
 
 

 
    Syntaksi:    
PythonC#:ssa minikeko voidaan toteuttaa käyttämällä PriorityQueue-luokkaa osoitteesta System.Collections.Generic namespace . PriorityQueue-luokka on prioriteettijono, joka tarjoaa tavan tallentaa elementtejä jonomaiseen tietorakenteeseen, jossa jokaiselle elementille on liitetty prioriteetti.
 
    Syntaksi:    
C# 
var minHeap = new PriorityQueue ();>> 
5. Min-keop JavaScriptissä
Vähimmäiskeko on binääripuu, jossa jokaisella solmulla on arvo pienempi tai yhtä suuri kuin sen lapsi. JavaScriptissä voit toteuttaa minikeon käyttämällä taulukkoa, jossa ensimmäinen elementti edustaa juurisolmua ja solmun lapsia indeksissä.    i    sijaitsevat indekseissä    2i+1    ja    2i+2.    
 
    Syntaksi:    
JavaScript    Ero Min-keon ja Max-keon välillä:      
 
 
 
Min Kasko
 
Max Heap
 
 
1.
 
Min-Keapissa juurisolmussa olevan avaimen on oltava pienempi tai yhtä suuri kuin kaikissa sen lapsissa olevien avainten joukossa.
 
Max-Keapissa juurisolmussa olevan avaimen on oltava suurempi tai yhtä suuri kuin kaikissa sen lapsissa olevien avainten joukossa.
 
 
2.
 
Min-Keapissa minimiavainelementti on juuressa.
alimerkkijono java
 
Max-Keapissa suurin avainelementti on juuressa.
 
 
3.
 
Min-Heap käyttää nousevaa prioriteettia.
 
Max-Heap käyttää laskevaa prioriteettia.
 
 
4.
 
Min-Heapin rakenteessa pienin elementti on etusijalla.
 
Max-Heapin rakenteessa suurin elementti on etusijalla.
 
 
5.
 
Min-keossa pienin elementti ponnahtaa ensimmäisenä kasasta.
 
Max-Keossa suurin elementti ponnahtaa kasasta ensimmäisenä.
 
Min-Heap-tietorakenteen sisäinen toteutus:
 
A    Vähimmäiskeko esitetään tyypillisesti taulukkona    .
 
Juurielementti on osoitteessa    Arr[0]    .
Kaikille i:lle solmulle    Arr[i]    :
    Arr[(i -1) / 2]    palauttaa yläsolmunsa.
    Arr[(2 * i) + 1]    palauttaa vasemman alisolmunsa.
    Arr[(2 * i) + 2]    palauttaa oikean lapsisolmunsa.
Min-Heapin sisäinen käyttöönotto vaatii kolme päävaihetta:
 
    Lisäys    : Jos haluat lisätä elementin minimikekoon, lisäämme elementin ensin taulukon loppuun ja säädämme sitten keon ominaisuutta vaihtamalla elementtiä toistuvasti emo-elementin kanssa, kunnes se on oikeassa paikassa.
    Poistaminen    : Jos haluat poistaa minimielementin min-keosta, vaihdamme ensin juurisolmun taulukon viimeiseen elementtiin, poistamme viimeisen elementin ja säädämme sitten keon ominaisuutta vaihtamalla elementtiä toistuvasti vaihtamalla elementtiä sen pienimmällä alatasolla, kunnes se on oikea asento.
    Kasata kasaan    : Kekotusoperaatiolla voidaan luoda minikeko lajittelemattomasta taulukosta.
Min-keap-tietorakenteen toiminnot ja niiden toteutus:
Tässä on joitain yleisiä toimintoja, jotka voidaan suorittaa keon tietorakenteelle,
 
1. Lisäys Min-Heap-tietorakenteeseen :
Elementit voidaan lisätä kasaan noudattamalla samanlaista lähestymistapaa kuin edellä on käsitelty poistoa varten. Ideana on:
 
Lisääminen min-keoon sisältää seuraavat vaiheet:
Lisää uusi elementti kasan loppuun, seuraavaan käytettävissä olevaan kohtaan puun viimeisellä tasolla.
Vertaa uutta elementtiä sen pääelementtiin. Jos yläelementti on suurempi kuin uusi elementti, vaihda ne.
Toista vaihetta 2, kunnes yläelementti on pienempi tai yhtä suuri kuin uusi elementti tai kunnes uusi elementti saavuttaa puun juuren.
Uusi elementti on nyt oikeassa paikassaan min-keossa ja kasan ominaisuus täyttyy.
    Kuva:    
iskcon täysi lomake
  
    Oletetaan, että kasa on Min-Heap:    
 
Lisäys Min-Heapiin
 
Lisäystoiminnon toteutus Min-Heapissa:
C++ 
#include  #include  using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & pino, int arvo) { // Lisää uusi elementti keon loppuun.push_back(value);  // Hae viimeisen elementin indeksi int index = heap.size() - 1;  // Vertaa uutta elementtiä sen emoelementtiin ja vaihda tarvittaessa // vaihtamalla (indeksi> 0 && pino[(indeksi - 1) / 2]> pino[index]) { swap(keko[index], kaso[(indeksi - 1) / 2]);  // Siirrä puussa ylös nykyisen // elementin yläpäähän index = (indeksi - 1) / 2;  } } // Pääfunktio insert_min_heap-funktion testaamiseen int main() { vektori pino;  int arvot[] = { 10, 7, 11, 5, 4, 13 };  int n = koko(arvot) / koko(arvot[0]);  for (int i = 0; i< n; i++) {  insert_min_heap(heap, values[i]);  cout << 'Inserted ' << values[i]  << ' into the min-heap: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  }  return 0; }>
 Java 
import java.util.*; public class GFG {  // Function to insert a new element into the min-heap  public static void insertMinHeap(int[] heap, int size,  int value)  {  // Add the new element to the end of the heap  heap[size] = value;  // Get the index of the last element  int index = size;  // Compare the new element with its parent and swap  // if necessary  while (index>0 && kasa[(indeksi - 1) / 2]> kasa[indeksi]) { swap(keko, indeksi, (indeksi - 1) / 2);  // Siirrä puussa ylös nykyisen // elementin yläpäähän index = (indeksi - 1) / 2;  } } // Toiminto vaihtaa kaksi elementtiä taulukossa public static void swap(int[] arr, int i, int j) { int temp = arr[i];  arr[i] = arr[j];  arr[j] = lämpötila;  } // Pääfunktio insertMinHeap-funktion testaamiseen public static void main(String[] args) { int[] kaso = new int[6];  int[] arvot = { 10, 7, 11, 5, 4, 13 };  int koko = 0;  for (int i = 0; i< values.length; i++) {  insertMinHeap(heap, size, values[i]);  size++;  System.out.print('Inserted ' + values[i]  + ' into the min-heap: ');  for (int j = 0; j < size; j++) {  System.out.print(heap[j] + ' ');  }  System.out.println();  }  } }>
 Python 3 
def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 ja kasa[(indeksi - 1) // 2]> kasa[indeksi]: kasa[indeksi], kaso[(indeksi - 1) // 2] = kasa[(indeksi - 1) // 2], kasa[ index] # Siirrä puussa ylös nykyisen elementin yläpäähän index = (indeksi - 1) // 2 pino = [] arvot = [10, 7, 11, 5, 4, 13] arvoille arvoissa: insert_min_heap( pino, arvo) print(f'Lisätty {arvo} min-keoon: {keko}')>
 C# 
using System; using System.Collections.Generic; public class Program {  // Function to insert a new element into the min-heap  static void InsertMinHeap(List pino, int arvo) { // Lisää uusi elementti keon loppuun.Add(arvo);  // Hae viimeisen elementin indeksi int index = heap.Count - 1;  // Vertaa uutta elementtiä sen emoelementtiin ja vaihda // tarvittaessa while (indeksi> 0 && kasa[(indeksi - 1) / 2]> pino[indeksi]) { int temp = pino[indeksi];  kasa[indeksi] = kasa[(indeksi - 1) / 2];  kasa[(indeksi - 1) / 2] = lämpötila;  // Siirrä puussa ylös nykyisen // elementin yläpäähän index = (indeksi - 1) / 2;  } } // Pääfunktio InsertMinHeap-funktion testaamiseen public static void Main() { List kasa = uusi lista ();  int[] arvot = { 10, 7, 11, 5, 4, 13 };  foreach(int arvo arvoissa) { InsertMinHeap(keko, arvo);  Console.Write('Lisätty ' + arvo + ' min-keoon: ');  foreach(int elementti kasassa) { Console.Write(element + ' ');  } Console.WriteLine();  } } }>
 Javascript 
function insertMinHeap(heap, value) {  heap.push(value);  let index = heap.length - 1;  let parentIndex = Math.floor((index - 1) / 2);  while (index>0 && pino[emoindeksi]> pino[indeksi]) { [keko[indeksi], keko[emoindeksi]] = [keko[emoindeksi], kaso[indeksi]];  indeksi = emoindeksi;  parentIndex = Math.floor((indeksi - 1) / 2);  } } // Käyttöesimerkki const heap = []; const-arvot = [10, 7, 11, 5, 4, 13]; for (arvojen jatkuva arvo) { insertMinHeap(keko, arvo);  console.log(`Lisätty ${value} min-keoon: ${heap}`); }>
   
  Lähtö  
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
 
    Aika monimutkaisuus: O(log(n)) (    missä n on keon elementtien lukumäärä    )     
    Aputila:    Päällä)
 
2. Poisto Min-Heap-tietorakenteessa :
Pienimmän elementin (juuren) poistaminen min-keosta. Juuri korvataan keon viimeisellä elementillä, ja sitten keon ominaisuus palautetaan vaihtamalla uusi juuri sen pienimmällä alatasolla, kunnes vanhempi on pienempi kuin molemmat alat tai kunnes uusi juuri saavuttaa lehtisolmun.
 
Korvaa poistettava juuri tai elementti viimeisellä elementillä.
Poista viimeinen elementti keosta.
Koska viimeinen elementti on nyt sijoitettu juurisolmun paikkaan. Joten se ei välttämättä seuraa keon ominaisuutta. Siksi kasaa viimeinen juuren paikkaan sijoitettu solmu.
    Kuva    :
käyttöliittymä javassa
  
    Oletetaan, että kasa on Min-Heap:    
  
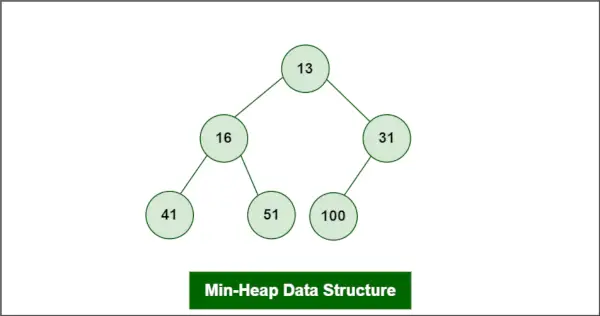
Min-Heap-tietorakenne
 
    Poistettava elementti on root, eli 13.    
 
    Käsitellä asiaa    :
 
Viimeinen elementti on 100.
 
    Vaihe 1:         Korvaa viimeinen elementti root-elementillä ja poista se.    
  
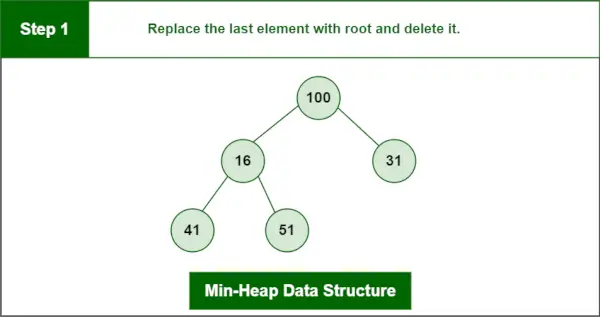
Min-Heap-tietorakenne
 
    Vaihe 2    :    Kasaa juuri.    
 
Viimeinen kasa:
  
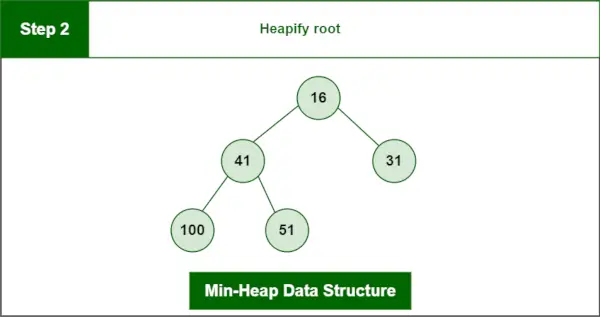
Min-Heap-tietorakenne
 
 
 
Poistotoiminnon toteutus Min-Heapissa:
C++ 
#include  #include  using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & pino, int arvo) { // Lisää uusi elementti keon loppuun.push_back(value);  // Hae viimeisen elementin indeksi int index = heap.size() - 1;  // Vertaa uutta elementtiä sen emoelementtiin ja vaihda tarvittaessa // vaihtamalla (indeksi> 0 && pino[(indeksi - 1) / 2]> pino[index]) { swap(keko[index], kaso[(indeksi - 1) / 2]);  // Siirrä puussa ylös nykyisen // elementin yläpäähän index = (indeksi - 1) / 2;  } } // Toiminto solmun poistamiseksi min-keosta void delete_min_heap(vector & pino, int arvo) { // Etsi poistettavan elementin indeksi int index = -1;  for (int i = 0; i< heap.size(); i++) {  if (heap[i] == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last  // element  heap[index] = heap[heap.size() - 1];  // Remove the last element  heap.pop_back();  // Heapify the tree starting from the element at the  // deleted index  while (true) {  int left_child = 2 * index + 1;  int right_child = 2 * index + 2;  int smallest = index;  if (left_child < heap.size()  && heap[left_child] < heap[smallest]) {  smallest = left_child;  }  if (right_child < heap.size()  && heap[right_child] < heap[smallest]) {  smallest = right_child;  }  if (smallest != index) {  swap(heap[index], heap[smallest]);  index = smallest;  }  else {  break;  }  } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() {  vector pino;  int arvot[] = { 13, 16, 31, 41, 51, 100 };  int n = koko(arvot) / koko(arvot[0]);  for (int i = 0; i< n; i++) {  insert_min_heap(heap, values[i]);  }  cout << 'Initial heap: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  delete_min_heap(heap, 13);  cout << 'Heap after deleting 13: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  return 0; }>
 Java 
import java.util.*; public class GFG {  // Function to insert a new element into the min-heap  public static void insertMinHeap(List pino, int arvo) { // Lisää uusi elementti keon loppuun.add(arvo);  // Hae viimeisen elementin indeksi int index = heap.size() - 1;  // Vertaa uutta elementtiä emoelementtiin ja vaihda // tarvittaessa while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (indeksi - 1) / 2);  // Siirrä puussa ylös nykyisen // elementin yläpäähän index = (indeksi - 1) / 2;  } } // Toiminto solmun poistamiseksi min-keosta julkisesta static void deleteMinHeap(List pino, int arvo) { // Etsi poistettavan elementin indeksi int index = -1;  for (int i = 0; i< heap.size(); i++) {  if (heap.get(i) == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last  // element  heap.set(index, heap.get(heap.size() - 1));  // Remove the last element  heap.remove(heap.size() - 1);  // Heapify the tree starting from the element at the  // deleted index  while (true) {  int leftChild = 2 * index + 1;  int rightChild = 2 * index + 2;  int smallest = index;  if (leftChild < heap.size()  && heap.get(leftChild)  < heap.get(smallest)) {  smallest = leftChild;  }  if (rightChild < heap.size()  && heap.get(rightChild)  < heap.get(smallest)) {  smallest = rightChild;  }  if (smallest != index) {  Collections.swap(heap, index, smallest);  index = smallest;  }  else {  break;  }  }  }  // Main function to test the insertMinHeap and  // deleteMinHeap functions  public static void main(String[] args)  {  List kasa = uusi ArrayList ();  int[] arvot = { 13, 16, 31, 41, 51, 100 };  int n = arvot.pituus;  for (int i = 0; i< n; i++) {  insertMinHeap(heap, values[i]);  }  System.out.print('Initial heap: ');  for (int j = 0; j < heap.size(); j++) {  System.out.print(heap.get(j) + ' ');  }  System.out.println();  deleteMinHeap(heap, 13);  System.out.print('Heap after deleting 13: ');  for (int j = 0; j < heap.size(); j++) {  System.out.print(heap.get(j) + ' ');  }  System.out.println();  } }>
 Python 3 
def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 ja kasa[(indeksi - 1) // 2]> kasa[indeksi]: kasa[indeksi], kaso[(indeksi - 1) // 2] = kasa[(indeksi - 1) // 2], kasa[ index] index = (indeksi - 1) // 2 def delete_min_heap(heap, value): index = -1 for i in range(len(heap)): if pino[i] == arvo: index = i break if index == -1: paluu pino[indeksi] = kaso[-1] kasa.pop() ja tosi: vasen_lapsi = 2 * indeksi + 1 oikea_lapsi = 2 * indeksi + 2 pienin = indeksi, jos vasen_lapsi< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)>
 C# 
using System; using System.Collections.Generic; class MinHeap {  private List kasa = uusi lista ();  public void Lisää(int arvo) { pino.Lisää(arvo);  int indeksi = kasa.Laskuri - 1;  while (indeksi> 0 && kasa[(indeksi - 1) / 2]> kasa[indeksi]) { Vaihda(indeksi, (indeksi - 1) / 2);  indeksi = (indeksi - 1) / 2;  } } public void Poista(int arvo) { int indeksi = pino.IndeksiOf(arvo);  if (indeksi == -1) { return;  } kasa[indeksi] = kasa[kasa.Laskuri - 1];  kasa.PoistaAt(kasa.Laskuri - 1);  while (tosi) { int vasenLapsi = 2 * indeksi + 1;  int rightLapsi = 2 * indeksi + 2;  int pienin = indeksi;  jos (vasenLapsi< heap.Count  && heap[leftChild] < heap[smallest]) {  smallest = leftChild;  }  if (rightChild < heap.Count  && heap[rightChild] < heap[smallest]) {  smallest = rightChild;  }  if (smallest != index) {  Swap(index, smallest);  index = smallest;  }  else {  break;  }  }  }  private void Swap(int i, int j)  {  int temp = heap[i];  heap[i] = heap[j];  heap[j] = temp;  }  public void Print()  {  for (int i = 0; i < heap.Count; i++) {  Console.Write(heap[i] + ' ');  }  Console.WriteLine();  } } class Program {  static void Main(string[] args)  {  MinHeap heap = new MinHeap();  int[] values = { 13, 16, 31, 41, 51, 100 };  for (int i = 0; i < values.Length; i++) {  heap.Insert(values[i]);  }  Console.Write('Initial heap: ');  heap.Print();  heap.Delete(13);  Console.Write('Heap after deleting 13: ');  heap.Print();  } }>
 Javascript 
function insertMinHeap(heap, value) {  // Add the new element to the end of the heap  heap.push(value);  // Get the index of the last element  let index = heap.length - 1;  // Compare the new element with its parent and swap if necessary  for (let flr = Math.floor((index - 1) / 2); index>0 && kasa[flr]> kasa[indeksi]; flr = Math.floor((indeksi - 1) / 2)) { [kasa[indeksi], kaso[flr]] = [ kasa[flr], kasa[indeksi], ];  // Siirrä puussa ylös nykyisen elementin yläpäähän index = Math.floor((indeksi - 1) / 2);  } } funktio deleteMinHeap(keko, arvo) { // Etsi poistettavan elementin indeksi anna index = -1;  for (olkoon i = 0; i< heap.length; i++) {  if (heap[i] == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last element  heap[index] = heap[heap.length - 1];  // Remove the last element  heap.pop();  // Heapify the tree starting from the element at the deleted index  while (true) {  let left_child = 2 * index + 1;  let right_child = 2 * index + 2;  let smallest = index;  if (left_child < heap.length && heap[left_child] < heap[smallest]) {  smallest = left_child;  }  if (right_child < heap.length && heap[right_child] < heap[smallest]) {  smallest = right_child;  }  if (smallest != index) {  [heap[index], heap[smallest]] = [heap[smallest], heap[index]];  index = smallest;  } else {  break;  }  } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) {  insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));>
   
  Lähtö  
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
 
    Aika monimutkaisuus    : O(log n) missä n on keon elementtien lukumäärä  
    Aputila:    Päällä)
 
3. Min-Heap-tietorakenteen kurkistustoiminto:
Minimielementin (eli keon juuren) saamiseksi palautetaan juurisolmun arvo. Kurkistamisen aikamonimutkaisuus min-keossa on O(1).
  
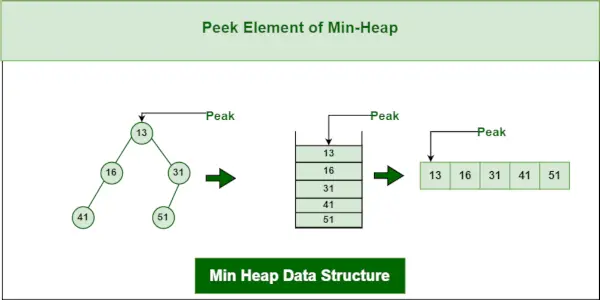
Vähimmäiskeon tietorakenne
 
Peek-operaation käyttöönotto Min-Heapissa:
C++ 
#include  #include  #include  using namespace std; int main() {  // Create a max heap with some elements using a  // priority_queue  priority_queue , suurempi > minHeap;  minHeap.push(9);  minHeap.push(8);  minHeap.push(7);  minHeap.push(6);  minHeap.push(5);  minHeap.push(4);  minHeap.push(3);  minHeap.push(2);  minHeap.push(1);  // Hanki huippuelementti (eli suurin elementti) int peakElement = minHeap.top();  // Tulosta huippuelementin cout<< 'Peak element: ' << peakElement << std::endl;  return 0; }>
 Java 
import java.util.PriorityQueue; public class GFG {  public static void main(String[] args)  {  // Create a max heap with some elements using a  // PriorityQueue  PriorityQueue minHeap = uusi PriorityQueue();  minHeap.add(9);  minHeap.add(8);  minHeap.add(7);  minHeap.add(6);  minHeap.add(5);  minHeap.add(4);  minHeap.add(3);  minHeap.add(2);  minHeap.add(1);  // Hanki huippuelementti (eli suurin elementti) int peakElement = minHeap.peek();  // Tulosta huippuelementti System.out.println('Peak element: ' + peakElement);  } }>
 Python 3 
import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)>
 C# 
using System; using System.Collections.Generic; public class GFG {  public static void Main()  {  // Create a min heap with some elements using a  // PriorityQueue  var minHeap = new PriorityQueue ();  minHeap.Enqueue(9);  minHeap.Enqueue(8);  minHeap.Enqueue(7);  minHeap.Enqueue(6);  minHeap.Enqueue(5);  minHeap.Enqueue(4);  minHeap.Enqueue(3);  minHeap.Enqueue(2);  minHeap.Enqueue(1);  // Hanki huippuelementti (eli pienin elementti) int peakElement = minHeap.Peek();  // Tulosta huippuelementti Console.WriteLine('Peak element: ' + peakElement);  } }>
 Javascript 
const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Hanki huippuelementti (eli pienin elementti) const peakElement = minHeap.peek(); // Tulosta huippuelementti console.log(`Peak element: ${peakElement}`);>>  
  Lähtö  
Peak element: 1>
  
    Aika monimutkaisuus    : Matriisin tai listan avulla toteutetussa min-keossa huippuelementtiin pääsee käsiksi vakioajassa, O(1), koska se sijaitsee aina keon juuressa.  
Binääripuulla toteutetussa min-keossa huippuelementtiin pääsee käsiksi myös O(1)-ajassa, koska se sijaitsee aina puun juuressa.
 
    Aputila:    Päällä)
 
4. Min-Keap-tietorakenteen kekotustoiminto:
Kasko-operaatiolla voidaan luoda minikeko lajittelemattomasta taulukosta. Tämä tehdään aloittamalla viimeisestä ei-lehtisolmusta ja suorittamalla toistuvasti kupla alas -toiminto, kunnes kaikki solmut täyttävät kasan ominaisuuden.
 
Heapify-toiminto Min Heapissa
 
    Heapify-operaation toteutus Min-Heapissa:    
C++ 
#include  #include  using namespace std; void minHeapify(vector &arr, int i, int n) { int pienin = i;  int l = 2*i + 1;  int r = 2*i + 2;  jos (l< n && arr[l] < arr[smallest])  smallest = l;  if (r < n && arr[r] < arr[smallest])  smallest = r;  if (smallest != i) {  swap(arr[i], arr[smallest]);  minHeapify(arr, smallest, n);  } } int main() {  vector arr = {10, 5, 15, 2, 20, 30};  cout<< 'Original array: ';  for (int i = 0; i < arr.size(); i++)  cout << arr[i] << ' ';  // Perform heapify operation on min-heap  for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size());  cout<< '
Min-Heap after heapify operation: ';  for (int i = 0; i < arr.size(); i++)  cout << arr[i] << ' ';  return 0; }>
 Java 
// Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main {  // Function to maintain the min-heap property of the heap rooted at index 'i'  public static void minHeapify(List arr, int i, int n) { // Oletetaan, että juuri on alun perin pienin alkio int pienin = i;  // Laske nykyisen solmun vasemman ja oikean lapsen indeksit int l = 2 * i + 1;  int r = 2 * i + 2;  // Vertaa vasenta lasta nykyiseen pienimpään if (l< n && arr.get(l) < arr.get(smallest))  smallest = l;  // Compare the right child with the current smallest  if (r < n && arr.get(r) < arr.get(smallest))  smallest = r;  // If the current node is not the smallest, swap it with the smallest child  if (smallest != i) {  int temp = arr.get(i);  arr.set(i, arr.get(smallest));  arr.set(smallest, temp);  // Recursively heapify the subtree rooted at the smallest child  minHeapify(arr, smallest, n);  }  }  public static void main(String[] args) {  // Create a list representing the array  List arr = Arrays.asList(10, 5, 15, 2, 20, 30);  System.out.print('Alkuperäinen taulukko: ');  // Tulosta alkuperäinen matriisi kohteelle (int i = 0; i< arr.size(); i++)  System.out.print(arr.get(i) + ' ');  // Perform heapify operation on the min-heap  // Start from the last non-leaf node and go up to the root of the tree  for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size());  System.out.print('
Min-Heap pinotuksen jälkeen: ');  // Tulosta min-keon kekotuksen jälkeen kohteelle (int i = 0; i< arr.size(); i++)  System.out.print(arr.get(i) + ' ');  } }>
 Python 
def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)>
 C# 
using System; using System.Collections.Generic; class GFG {  // Function to perform the minHeapify operation on a min-heap.  static void MinHeapify(List arr, int i, int n) { int pienin = i;  int vasen = 2 * i + 1;  int oikea = 2 * i + 2;  // Vertaa vasenta alaosaa nykyiseen pienimpään solmuun.  jos (vas< n && arr[left] < arr[smallest])  smallest = left;  // Compare the right child with the current smallest node.  if (right < n && arr[right] < arr[smallest])  smallest = right;  // If the current node is not the smallest  // swap it with the smallest child.  if (smallest != i)  {  int temp = arr[i];  arr[i] = arr[smallest];  arr[smallest] = temp;  // Recursively call minHeapify on the affected subtree.  MinHeapify(arr, smallest, n);  }  }  static void Main(string[] args)  {  List arr = uusi lista { 10, 5, 15, 2, 20, 30 };  Console.Write('Alkuperäinen taulukko: ');  foreach (int num in arr) Console.Write(num + ' ');  // Suorita kasaantumisoperaatio min-keossa.  for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count);  Console.Write('
Min-Heap kekotustoiminnon jälkeen: ');  foreach (int num in arr) Console.Write(num + ' ');  } }>
 Javascript 
// Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) {  let smallest = i;  let l = 2 * i + 1;  let r = 2 * i + 2;  // Check if left child is smaller than the current smallest element  if (l < n && arr[l] < arr[smallest])  smallest = l;  // Check if right child is smaller than the current smallest element  if (r < n && arr[r] < arr[smallest])  smallest = r;  // If the smallest element is not the current element, swap them  if (smallest !== i) {  [arr[i], arr[smallest]] = [arr[smallest], arr[i]];  minHeapify(arr, smallest, n);  } } // Main function function main() {  const arr = [10, 5, 15, 2, 20, 30];  // Print the original array  console.log('Original array: ' + arr.join(' '));  // Perform heapify operation on the min-heap  for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length);  // Tulosta min-keon keonmuodostusoperaation jälkeen console.log('Min-Heap pinonmuodostuksen jälkeen: ' + arr.join(' ')); } // Kutsu main-funktiota aloittaaksesi prosessin main();>>  
  Lähtö  Min-keon kasan aikamonimutkaisuus on O(n).
 
5. Hakutoiminto Min-Heap-tietorakenteessa:
Elementin etsimiseksi min-keosta voidaan suorittaa lineaarinen haku kasaa edustavan taulukon yli. Lineaarisen haun aikamonimutkaisuus on kuitenkin O(n), mikä ei ole tehokasta. Siksi etsiminen ei ole yleisesti käytetty operaatio min kasossa.
 
Tässä on esimerkkikoodi, joka näyttää, kuinka voit etsiä elementtiä minimikekosta käyttämällä    std::find()    :
shloka mehta koulutus
C++ 
#include  using namespace std; int main() {  priority_queue , suurempi > min_heap;  // esimerkki max kasa min_heap.push(10);  min_heap.push(9);  min_heap.push(8);  min_heap.push(6);  min_heap.push(4);  int elementti = 6; // elementti, josta etsitään bool löytyi = false;  // Kopioi minimikeko väliaikaiseen jonoon ja etsi // elementti std::priority_queue , suurempi > lämpötila = min_keko;  while (!temp.empty()) { if (temp.top() == elementti) { löytyi = tosi;  tauko;  } temp.pop();  } if (löytyi) { std::cout<< 'Element found in the min heap.'  << std::endl;  }  else {  std::cout << 'Element not found in the min heap.'  << std::endl;  }  return 0; }>
 Java 
import java.util.PriorityQueue; public class GFG {  public static void main(String[] args)  {  PriorityQueue min_heap = uusi PriorityQueue();  min_heap.add(3); // lisää elementtejä prioriteettijonoon min_heap.offer(1);  min_kean.tarjous(4);  min_kean.tarjous(1);  min_kean.tarjous(6);  int elementti = 6; // elementti, jolla etsitään loogista löydetty = false;  // Kopioi minimikeko väliaikaiseen jonoon ja etsi // elementti PriorityQueue temp = uusi PriorityQueue(min_keko);  while (!temp.isEmpty()) { if (temp.poll() == elementti) { löytyi = tosi;  tauko;  } } if (löytyi) { System.out.println( 'Elementti löytyi minikeosta.');  } else { System.out.println( 'Elementtiä ei löydy min-keosta.');  } } }>
 Python 3 
import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')>
 C# 
using System; using System.Collections.Generic; public class GFG {  public static void Main()  {  var minHeap = new PriorityQueue ();  // esimerkki min-keko minHeap.Enqueue(4);  minHeap.Enqueue(6);  minHeap.Enqueue(8);  minHeap.Enqueue(9);  minHeap.Enqueue(10);  int elementti = 6; // elementti, josta etsitään bool löytyi = false;  // Kopioi minimikeko väliaikaiseen jonoon ja etsi // elementti var temp = new PriorityQueue (minHeap);  while (temp.Count> 0) { if (temp.Peek() == elementti) { löytyi = tosi;  tauko;  } temp.Dequeue();  } if (löytyi) { Console.WriteLine( 'Elementti löytyi minikeosta.');  } else { Console.WriteLine( 'Elementtiä ei löydy min-keosta.');  } } }>
 Javascript 
// Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == elementti) { löytyi = tosi;  tauko;  } temp.dequeue(); } if (löytyi) { console.log('Elementti löytyi minimikeosta.'); } else { console.log('Elementtiä ei löydy min-keosta.'); }>
   
  Lähtö  The    aika monimutkaisuus    tästä ohjelmasta on    O(n log n)    , missä    n    on prioriteettijonon elementtien lukumäärä.
 
Lisäystoiminnolla on aika monimutkaisuus    O(log n)    pahimmassa tapauksessa, koska kasan omaisuus on säilytettävä. Hakutoiminto sisältää prioriteetin jonon kopioimisen väliaikaiseen jonoon ja sitten väliaikaisen jonon läpikäymisen, mikä vie    O(n log n)    pahimmassa tapauksessa aikaa, koska jokainen elementti on kopioitava ja pompattava jonosta ja prioriteettijono on rakennettava uudelleen jokaista toimintoa varten.
 
The    tilan monimutkaisuus    ohjelmasta on    Päällä)    koska se varastoi    n    elementit prioriteettijonossa ja luo väliaikaisen jonon kanssa    n    elementtejä.
 
Min-Heap-tietorakenteen sovellukset:
    Keon lajittelu:    Vähimmäiskekoa käytetään avainkomponenttina keon lajittelualgoritmissa, joka on tehokas lajittelualgoritmi, jonka aikamonimutkaisuus on O(nlogn).
    Prioriteettijono:    Prioriteettijono voidaan toteuttaa käyttämällä min-keon tietorakennetta, jossa pienimmän arvon omaava elementti on aina juuressa.
    Dijkstran algoritmi:    Dijkstran algoritmissa minikekoa käytetään tallentamaan graafin kärjet minimietäisyydellä aloituspisteestä. Piste, jolla on pienin etäisyys, on aina kasan juuressa.
    Huffman koodaus:    Huffman-koodauksessa minimikekoa käytetään toteuttamaan prioriteettijono optimaalisen etuliitekoodin rakentamiseksi tietylle merkkijoukolle.
    Yhdistä K-lajitellut taulukot:    K-lajiteltujen taulukoiden avulla voimme yhdistää ne yhdeksi lajiteltuun taulukkoon tehokkaasti käyttämällä minikeon tietorakennetta.
Min-keap-tietorakenteen edut:
    Tehokas lisäys ja poisto    : Vähimmäiskeko mahdollistaa elementtien nopean lisäämisen ja poistamisen aikamonimutkaisuuden ollessa O(log n), missä n on keon elementtien lukumäärä.
    Tehokas minimielementin haku:    Minimikeon minimielementti on aina keon juuressa, joka voidaan noutaa O(1) ajassa.
    Tilatehokas:    Min-keo on kompakti tietorakenne, joka voidaan toteuttaa taulukon tai binääripuun avulla, mikä tekee siitä tilatehokkaan.
    Lajittelu:    Min-keon avulla voidaan toteuttaa tehokas lajittelualgoritmi, kuten keon lajittelu, jonka aikamonimutkaisuus on O(n log n).
    Prioriteettijono:    Min-keon avulla voidaan toteuttaa prioriteettijono, jossa minimiprioriteetin omaava elementti voidaan noutaa tehokkaasti O(1)-ajassa.
    Monipuolisuus:    Min heapilla on useita sovelluksia tietojenkäsittelytieteessä, mukaan lukien graafialgoritmit, tietojen pakkaus ja tietokantajärjestelmät.
Kaiken kaikkiaan min heap on hyödyllinen ja monipuolinen tietorakenne, joka tarjoaa tehokkaan toiminnan, tilatehokkuuden ja jolla on useita sovelluksia tietojenkäsittelytieteessä.