Javassa, Kaavio on tietorakenne, joka tallentaa tiettyä dataa. Käsite kaavio on varastettu matematiikasta, joka täyttää tietojenkäsittelytieteen alan tarpeet. Se edustaa verkkoa, joka yhdistää useita pisteitä toisiinsa. Tässä osiossa opimme yksityiskohtaisesti Java Graph -tietorakenteen. Lisäksi opimme graafin tyypit , niiden täytäntöönpano ja läpikulku kaavion yli.
Kaavio
A kaavio on graafinen terminologia
Vertex: Vertices ovat piste, joka yhdistää reunat. Se edustaa dataa. Se tunnetaan myös solmuna. Se on merkitty ympyrällä ja se on merkittävä. Graafin muodostamiseksi täytyy olla vähintään solmu. Esimerkiksi talo, bussipysäkki jne.
Reuna: Reuna on viiva, joka yhdistää kaksi kärkeä. Se edustaa kärkien välistä suhdetta. Reunat on merkitty viivalla. Esimerkiksi polku bussipysäkille talostasi.
Paino: Se on merkitty reunaan asti. Esimerkiksi kahden kaupungin välinen etäisyys on 100 km, jolloin etäisyyttä kutsutaan reunan painoksi.
Polku: Polku on tapa päästä määränpäähän sarjan alkupisteestä.
Graafisten tyypit
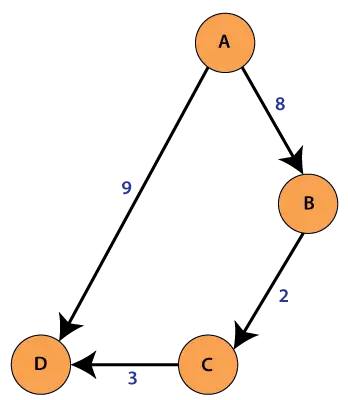




Yhdistettyjä kaavioita on kahdenlaisia.






Java Graph -toteutus
Kaavioiden toteuttamiseen Java aiomme käyttää Yleinen luokkaa. Luodaksemme Java Generic -luokan objektin käytämme seuraavaa syntaksia:
BaseType obj = new BaseType ();
Muista, että emme voi käyttää primitiivityyppiä parametrityypillä.
Luodaan Java-ohjelma, joka toteuttaa Graphin.
GraphImplementation.java
import java.util.*; class Graph { //creating an object of the Map class that stores the edges of the graph private Map<t, list> map = new HashMap(); //the method adds a new vertex to the graph public void addNewVertex(T s) { map.put(s, new LinkedList()); } //the method adds an edge between source and destination public void addNewEdge(T source, T destination, boolean bidirectional) { // if (!map.containsKey(source)) addNewVertex(source); if (!map.containsKey(destination)) addNewVertex(destination); map.get(source).add(destination); if (bidirectional == true) { map.get(destination).add(source); } } //the method counts the number of vertices public void countVertices() { System.out.println('Total number of vertices: '+ map.keySet().size()); } //the method counts the number of edges public void countEdges(boolean bidirection) { //variable to store number of edges int count = 0; for (T v : map.keySet()) { count = count + map.get(v).size(); } if (bidirection == true) { count = count / 2; } System.out.println('Total number of edges: '+ count); } //checks a graph has vertex or not public void containsVertex(T s) { if (map.containsKey(s)) { System.out.println('The graph contains '+ s + ' as a vertex.'); } else { System.out.println('The graph does not contain '+ s + ' as a vertex.'); } } //checks a graph has edge or not //where s and d are the two parameters that represent source(vertex) and destination (vertex) public void containsEdge(T s, T d) { if (map.get(s).contains(d)) { System.out.println('The graph has an edge between '+ s + ' and ' + d + '.'); } else { System.out.println('There is no edge between '+ s + ' and ' + d + '.'); } } //prints the adjacencyS list of each vertex //here we have overridden the toString() method of the StringBuilder class @Override public String toString() { StringBuilder builder = new StringBuilder(); //foreach loop that iterates over the keys for (T v : map.keySet()) { builder.append(v.toString() + ': '); //foreach loop for getting the vertices for (T w : map.get(v)) { builder.append(w.toString() + ' '); } builder.append('
'); } return (builder.toString()); } } //creating a class in which we have implemented the driver code public class GraphImplementation { public static void main(String args[]) { //creating an object of the Graph class Graph graph=new Graph(); //adding edges to the graph graph.addNewEdge(0, 1, true); graph.addNewEdge(0, 4, true); graph.addNewEdge(1, 2, true); graph.addNewEdge(1, 3, false); graph.addNewEdge(1, 4, true); graph.addNewEdge(2, 3, true); graph.addNewEdge(2, 4, true); graph.addNewEdge(3, 0, true); graph.addNewEdge(2, 0, true); //prints the adjacency matrix that represents the graph System.out.println('Adjacency List for the graph:
'+ graph.toString()); //counts the number of vertices in the graph graph.countVertices(); //counts the number of edges in the graph graph.countEdges(true); //checks whether an edge is present or not between the two specified vertices graph.containsEdge(3, 4); graph.containsEdge(2, 4); //checks whether vertex is present or not graph.containsVertex(3); graph.containsVertex(5); } } </t,> Lähtö:

Suunnatun graafin toteutus
DirectedGraph.java
aakkoset ja numerot
import java.util.*; //Creating a class named Edge that stores the edges of the graph class Edge { //the variable source and destination represent the vertices int s, d; //creating a constructor of the class Edge Edge(int s, int d) { this.s = s; this.d = d; } } //a class to represent a graph object class Graph { //note that we have created an adjacency list (i.e. List of List) List<list> adjlist = new ArrayList(); //creating a constructor of the class Graph that construct a graph public Graph(List edges) { int n = 0; //foreach loop that iterates over the edge for (Edge e: edges) { //determines the maximum numbered vertex n = Integer.max(n, Integer.max(e.s, e.d)); } //reserve the space for the adjacency list for (int i = 0; i <= 1 n; i++) { adjlist.add(i, new arraylist()); } adds the edges to undirected graph for (edge current: edges) allocate node in adjacency list from source destination adjlist.get(current.s).add(current.d); function print representation of a public static void showgraph(graph graph) int s="0;" determines size n="graph.adjlist.size();" while (s ' + d ') '); system.out.println(); increments by s++; implementing driver code class directedgraph main (string args[]) creating edge(0, 1), edge(1, 2), edge(2, 4), edge(4, 1),new edge(3, 5), edge(5, 1)); construct given graph(edges); prints that represents graph.showgraph(graph); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-13.webp" alt="Java Graph"> <h2>Implementation of Weighted Graph</h2> <p> <strong>WeightedGraph.java</strong> </p> <pre> import java.util.*; //the class stores the edges of the graph class Edge { int s, d, w; //creating a constructor of the class Edge Edge(int src, int dest, int weight) { this.s = src; this.d = dest; this.w = weight; } } //a class to store adjacency list nodes class Node { int value, weight; //creating a constructor of the class Vertex Node(int value, int weight) { this.value = value; this.weight = weight; } //overrides the toString() method @Override public String toString() { return this.value + ' (' + this.weight + ')'; } } //a class to represent a graph object class Graph { //note that we have created an adjacency list (i.e. List of List) List<list> adjlist = new ArrayList(); //creating a constructor of the class Graph that creates graph public Graph(List edges) { //find the maximum numbered vertex int n = 0; //iterates over the edges of the graph for (Edge e: edges) { //determines the maximum numbered vertex n = Integer.max(n, Integer.max(e.s, e.d)); } //reserve the space for the adjacency list for (int i = 0; i <= 1 n; i++) { adjlist.add(i, new arraylist()); } adds the edges to undirected graph for (edge e: edges) creating a node (from source destination) in adjacency list adjlist.get(e.s).add(new node(e.d, e.w)); uncomment following statement adj.get(e.dest).add(new node(e.src, e.weight)); method that prints of public static void printgraph(graph graph) int src="0;" n="graph.adjlist.size();" system.out.printf('adjacency is: '); while (src %s ', src, edge); system.out.println(); increments by src++; implementing driver code class weightedgraph main (string args[]) with their associated weight edge(1, 4, 3), edge(4, 2, 5), edge(2, 5, 10), edge(5, 1, 6), edge(3, 9), 1), 2)); creates declared above graph(edges); corresponding graph.printgraph(graph); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-14.webp" alt="Java Graph"> <h2>Graph Traversal</h2> <p>Traversal over the graph means visit each and every vertex and edge at least once. To traverse over the graph, Graph data structure provides two algorithms:</p> <ul> <li>Depth-First Search (DFS)</li> <li>Breadth-First Search (DFS)</li> </ul> <h3>Depth-First Search (DFS)</h3> <p> <a href="/dfs-algorithm">DFS algorithm</a> is a recursive algorithm that is based on the backtracking concept. The algorithm starts from the initial node and searches in depth until it finds the goal node (a node that has no child). Backtracking allows us to move in the backward direction on the same path from which we have traversed in the forward direction.</p> <p>Let's implement the DFS algorithm in a Java program.</p> <p> <strong>DepthFirstSearch.java</strong> </p> <pre> import java.io.*; import java.util.*; //creates an undirected graph class Graph { //stores the number of vertices private int Vertices; //creates a linked list for the adjacency list of the graph private LinkedList adjlist[]; //creating a constructor of the Graph class Graph(int count_v) { //assigning the number of vertices to the passed parameter Vertices = count_v; adjlist = new LinkedList[count_v]; //loop for creating the adjacency lists for (int i=0; i<count_v; 3 10 ++i) adjlist[i]="new" linkedlist(); } method that adds a new edge to the graph void addnewedge(int v, int w) { adjlist[v].add(w); add w v's list. logic of dfs traversal starts from root node traversaldfs(int boolean vnodelist[]) if current (root node) is visited, it vnodelist vnodelist[v]="true;" system.out.print(v+' '); detrmines negihboring nodes iterates over list iterator i="adjlist[v].listIterator();" while (i.hasnext()) returns next element in iteration and store variable n (!vnodelist[n]) calling function performs depth first traversaldfs(n, vnodelist); dfs(int v) creates an array type for visited initially all are unvisited visited[]="new" boolean[vertices]; call recursive traversaldfs() traversaldfs(v, visited); implementing driver code public class depthfirstsearch static main(string args[]) having vertices g="new" graph(10); edges g.addnewedge(1, 2); g.addnewedge(2, 3); g.addnewedge(3, 4); g.addnewedge(4, 5); g.addnewedge(5, 7); 6); print sequencnce which bfs done system.out.println('depth-first is: (as g.dfs(1); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-15.webp" alt="Java Graph"> <h3>Breadth First Search (BFS)</h3> <p> <a href="/bfs-algorithm">BFS algorithm</a> is the most common approach to traverse over the graph. The traversal starts from the source node and scans its neighboring nodes (child of the current node). In short, traverse horizontally and visit all the nodes of the current layer. After that, move to the next layer and perform the same.</p> <p>Let's implement the BFS algorithm in a Java program.</p> <p> <strong>BreadthFirstSearch.java</strong> </p> <pre> import java.io.*; import java.util.*; //creates an undirected graph class Graph { //stores the number of vertices private int vertices; //creates a linked list for the adjacency list of the graph private LinkedList adjlist[]; //creating a constructor of the Graph class Graph(int count_v) { //assigning the number of vertices to the passed parameter vertices = count_v; adjlist = new LinkedList[count_v]; //loop for creating the adjacency lists for (int i=0; i<count_v; 10 ++i) adjlist[i]="new" linkedlist(); } method that adds a new edge to the graph void addnewedge(int v, int w) { adjlist[v].add(w); traversal starts from root node traversalbfs(int rnode) creates an array of boolean type for visited initially all nodes are unvisited visitednode[]="new" boolean[vertices]; creating another list storing linkedlist vnodelist="new" if current (root node) is visited, add it visitednode[rnode]="true;" inserts into vnodelist.add(rnode); while loop executes until we have (vnodelist.size() !="0)" deque entry queue and process poll() retrieves removes head (first element) this rnode="vnodelist.poll();" system.out.print(rnode+' '); detrmines negihboring iterates over iterator i="adjlist[rnode].listIterator();" (i.hasnext()) returns next element in iteration store variable n checks or not (!visitednode[n]) above if-statement true, visits visitednode[n]="true;" vnodelist.add(n); implementing driver code public class breadthfirstsearch static main(string args[]) having vertices graph(10); edges graph.addnewedge(2, 5); graph.addnewedge(3, graph.addnewedge(1, 2); 4); graph.addnewedge(4, 1); graph.addnewedge(6, graph.addnewedge(5, 6); 3); graph.addnewedge(7, 7); print sequence which bfs execute system.out.println('breadth-first is: graph.traversalbfs(2); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-16.webp" alt="Java Graph"> <hr></count_v;></pre></count_v;></pre></=></list></pre></=></list>