Lineaarinen ohjelmointi on matemaattinen käsite, jota käytetään lineaarifunktion optimaalisen ratkaisun löytämiseen. Tämä menetelmä käyttää yksinkertaisia oletuksia annetun funktion optimointiin. Lineaarisella ohjelmoinnilla on valtava reaalimaailman sovellus ja sitä käytetään erilaisten ongelmien ratkaisemiseen.
Lineaarista ohjelmointia käytetään useilla toimialoilla, kuten laivateollisuudessa, valmistusteollisuudessa, kuljetusteollisuudessa, televiestinnässä ja muilla.
Termi lineaarinen ohjelmointi koostuu kahdesta sanasta lineaarinen ja ohjelmointi, sana lineaarinen kertoo ongelmassa käytettyjen erityyppisten ykkösasteisten muuttujien välisen suhteen ja sana ohjelmointi kertoo vaiheittaisen prosessin näiden ongelmien ratkaisemiseksi.
Tässä artikkelissa opimme yksityiskohtaisesti lineaarisesta ohjelmoinnista, sen esimerkeistä, kaavoista ja muista käsitteistä.
Sisällysluettelo
- Mitä on lineaarinen ohjelmointi?
- Lineaarisen ohjelmoinnin komponentit
- Lineaarisen ohjelmoinnin esimerkkejä
- Lineaarisen ohjelmoinnin ongelmat
- Lineaarisen ohjelmoinnin ongelmien tyypit
- Lineaarinen ohjelmointikaava
- Kuinka ratkaista lineaarisen ohjelmoinnin ongelmia?
- Lineaariset ohjelmointimenetelmät
- Lineaarinen ohjelmointi Simplex-menetelmä
- Lineaarinen ohjelmoinnin graafinen menetelmä
- Lineaariset ohjelmointisovellukset
- Lineaarisen ohjelmoinnin merkitys
- Lineaarisen ohjelmoinnin ajantasaiset sovellukset
- Lineaarinen ohjelmointi operaatiotutkimuksessa
- Yksinkertainen menetelmä
Mitä on lineaarinen ohjelmointi?
Lineaarinen ohjelmointi tai Lineaarinen optimointi on tekniikka, joka auttaa meitä löytämään optimaalisen ratkaisun tietylle ongelmalle, optimaalinen ratkaisu on ratkaisu, joka on paras mahdollinen lopputulos tietylle ongelmalle.
Yksinkertaisesti sanottuna se on tapa saada selville, miten jotain tehdään parhaalla mahdollisella tavalla. Rajallisilla resursseilla sinun on käytettävä resursseja optimaalisesti ja saavutettava paras mahdollinen tulos tietyssä tavoitteessa, kuten pienin kustannukset, korkein marginaali tai vähiten aikaa.
Tilanne, joka vaatii tiettyjen rajoitusten alaisten muuttujien parhaiden arvojen etsimistä, on tilanne, jossa käytämme lineaarisia ohjelmointitehtäviä. Näitä tilanteita ei voida käsitellä tavallisilla laskennalla ja numeerisilla tekniikoilla.
Lineaarisen ohjelmoinnin määritelmä
Lineaarinen ohjelmointi on tekniikka, jota käytetään tietyn skenaarion optimointiin. Lineaarisen ohjelmoinnin käyttö antaa meille parhaan mahdollisen lopputuloksen tietyssä tilanteessa. Se käyttää kaikkia käytettävissä olevia resursseja siten, että ne tuottavat optimaalisen tuloksen.
Lineaarisen ohjelmoinnin komponentit
Lineaarisen ohjelmoinnin (LP) ongelman peruskomponentit ovat:
- Päätösmuuttujat: Muuttujat, jotka haluat määrittää optimaalisen ratkaisun saavuttamiseksi.
- Tavoitetehtävä: M atemaattinen yhtälö, joka edustaa tavoitetta, jonka haluat saavuttaa
- Rajoitukset: Rajoitukset, joita päätösmuuttujien on noudatettava.
- Ei-negatiivisuuden rajoitukset: Joissakin tosielämän skenaarioissa, päätösmuuttujat eivät voi olla negatiivisia
Lineaarisen ohjelmoinnin lisäominaisuudet
- Rajallisuus: Päätösmuuttujien ja rajoitusten määrä LP-tehtävässä on äärellinen.
- Lineaarisuus: Tavoitefunktion ja kaikkien rajoitusten on oltava päätösmuuttujien lineaarisia funktioita . Se tarkoittaa, että muuttujien asteen tulee olla yksi.
Lineaarisen ohjelmoinnin esimerkkejä
Pystymme ymmärtämään tilanteet, joissa lineaarista ohjelmointia sovelletaan alla käsitellyn esimerkin avulla,
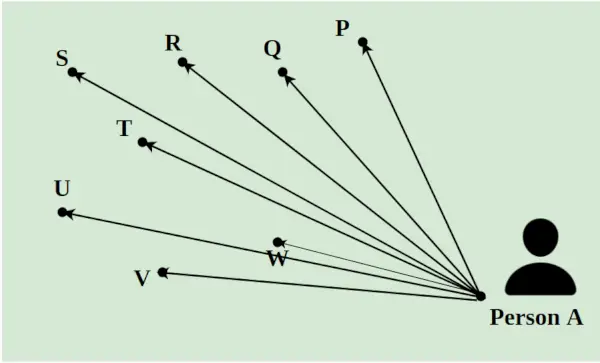
Oletetaan, että jakelumiehen on toimitettava 8 pakettia päivässä kaupungin eri paikkoihin. Hänen on poimittava kaikki paketit A:sta ja toimitettava ne pisteisiin P, Q, R, S, T, U, V ja W. Niiden välinen etäisyys osoitetaan alla olevan kuvan viivoilla. Lyhin tie, jota toimitusmies seuraa, lasketaan käyttämällä lineaarisen ohjelmoinnin käsitettä.
git status -s
Lineaarisen ohjelmoinnin ongelmat
Lineaariset ohjelmointiongelmat (LPP) sisältää lineaarisen funktion optimoinnin funktion optimaalisen arvoratkaisun löytämiseksi. Optimaalinen arvo voi olla joko enimmäisarvo tai pienin arvo.
LPP:ssä lineaarisia funktioita kutsutaan tavoitefunktiot. Tavoitefunktiolla voi olla useita muuttujia, jotka ovat ehtojen alaisia ja joiden on täytettävä lineaariset rajoitukset .
Lineaarisen ohjelmoinnin ongelmien tyypit
On olemassa monia erilaisia lineaarisen ohjelmoinnin ongelmia (LPP), mutta käsittelemme tässä artikkelissa kolmea suurta lineaarista ohjelmointiongelmaa.
Valmistusongelmat
Valmistusongelmat ovat ongelma, joka koskee yksiköiden määrää, joka tulisi tuottaa tai myydä voiton maksimoimiseksi, kun jokainen tuote vaatii kiinteää työvoimaa, konetunteja ja raaka-aineita.
Ruokavalio-ongelmat
Sitä käytetään ruokavalioon sisällytettävien erilaisten ainesosien määrän laskemiseen vähimmäiskustannusten saamiseksi elintarvikkeiden saatavuuden ja hintojen mukaan.
Kuljetusongelmat
Sitä käytetään kuljetusaikataulujen määrittämiseen, jotta löydetään halvin tapa kuljettaa tuote eri paikoissa sijaitsevilta tehtailta/tehtailta eri markkinoille.
Lineaarinen ohjelmointikaava
Lineaarinen ohjelmointiongelma koostuu
- Päätöksen muuttujat
- Objektiivinen toiminto
- Rajoitukset
- Ei-negatiiviset rajoitukset
Päätöksen muuttujat ovat muuttujat x ja y, jotka päättävät lineaarisen ohjelmointitehtävän lähdön ja edustavat lopullista ratkaisua.
The tavoitefunktio , jota yleensä edustaa Z, on lineaarinen funktio, joka on optimoitava annetun ehdon mukaan lopullisen ratkaisun saamiseksi.
The rajoituksia Päätösmuuttujia, jotka rajoittavat niiden arvoja, kutsutaan rajoituksiksi.
Lineaarisen ohjelmointiongelman yleinen kaava on nyt
Objektiivinen toiminto : Z = kirves + by
Rajoitukset: cx + dy ≥ e, px + qy ≤ r
Ei-negatiiviset rajoitukset: x ≥ 0, y ≥ 0
Yllä olevassa ehdossa x ja y ovat päätösmuuttujia.
Kuinka ratkaista lineaarisen ohjelmoinnin ongelmia?
Ennen lineaarisen ohjelmoinnin tehtävien ratkaisemista meidän on ensin muotoiltava tehtävät standardiparametrien mukaan. Lineaarisen ohjelmoinnin ongelmien ratkaisemisen vaiheet ovat
Vaihe 1: Merkitse ratkaisumuuttujat tehtävään.
Vaihe 2: Rakenna tehtävän tavoitefunktio ja tarkista, pitääkö funktio minimoida vai maksimoida.
Vaihe 3: Kirjoita muistiin kaikki lineaaristen tehtävien rajoitteet.
Vaihe 4: Varmista päätösmuuttujien ei-negatiiviset rajoitukset.
Vaihe 5: Ratkaise nyt lineaarisen ohjelmoinnin ongelma millä tahansa menetelmällä, yleensä käytämme joko simpleksi- tai graafista menetelmää.
Lineaariset ohjelmointimenetelmät
Käytämme erilaisia menetelmiä lineaarisen ohjelmoinnin ongelmien ratkaisemiseen. Kaksi yleisintä käytettyä menetelmää ovat
- Yksinkertainen menetelmä
- Graafinen menetelmä
Opitaanpa näistä kahdesta menetelmästä yksityiskohtaisesti tässä artikkelissa,
Lineaarinen ohjelmointi Simplex-menetelmä
Yksi yleisimmistä menetelmistä lineaarisen ohjelmoinnin ongelman ratkaisemiseksi on simpleksimenetelmä. Tässä menetelmässä toistamme tietyn ehdon 'n' useita kertoja, kunnes saavutetaan optimaalinen ratkaisu.
Lineaarisen ohjelmoinnin ongelmien ratkaisemiseen simplex-menetelmällä vaadittavat vaiheet ovat:
Vaihe 1: Muotoile lineaarisen ohjelmoinnin tehtävät annettujen rajoitusten perusteella.
Vaihe 2: Muunna kaikki annetut epäyhtälöt lineaaristen ohjelmointiongelmien yhtälöiksi tai yhtälöiksi lisäämällä löysä muuttuja jokaiseen epäyhtälöön aina tarvittaessa.
Vaihe 3: Muodosta alkuperäinen simpleksitaulukko. Esittämällä jokainen rajoitusyhtälö rivillä ja kirjoittamalla tavoitefunktio alimmalle riville. Näin saatua taulukkoa kutsutaan Simplex-taulukoksi.
Vaihe 4: Tunnista alarivin suurin negatiivinen merkintä, sen elementin saraketta, jolla on suurin negatiivinen merkintä, kutsutaan pivot-sarakkeeksi
Vaihe 5: Jaa oikeanpuoleisen sarakkeen merkinnät vastaavan pivot-sarakkeen merkintöihin, pois lukien alimman rivin merkinnät. Nyt sitä riviä, joka sisältää vähiten merkinnän, kutsutaan pivot-riviksi. Pivot-elementti saadaan pivot-rivin ja sarakkeen leikkauspisteestä.
Vaihe 6: Tee matriisioperaatiolla ja pivot-elementin avulla kaikki pivot-sarakkeen merkinnät nollaksi.
Vaihe 7: Tarkista ei-negatiiviset merkinnät alimmalla rivillä, jos alimmalla rivillä ei ole negatiivisia merkintöjä, lopeta prosessi tai aloita prosessi uudelleen vaiheesta 4.
Vaihe 8: Näin saatu lopullinen simpleksitaulukko antaa ratkaisun ongelmaamme.
Lineaarinen ohjelmoinnin graafinen menetelmä
Graafinen menetelmä on toinen menetelmä kuin Simplex-menetelmä, jota käytetään lineaaristen ohjelmointiongelmien ratkaisemiseen. Kuten nimestä voi päätellä, tämä menetelmä käyttää kaavioita annettujen lineaaristen ohjelmointiongelmien ratkaisemiseen. Tämä on paras tapa ratkaista lineaarisen ohjelmoinnin ongelmia ja vaatii vähemmän vaivaa kuin simpleksimenetelmä.
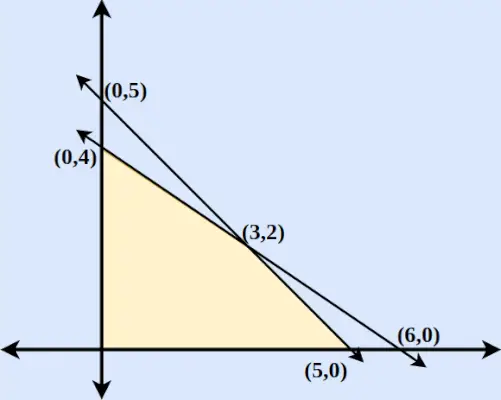
Tätä menetelmää käytettäessä piirrämme kaikki epäyhtälöt annetuissa lineaarisissa ohjelmointitehtävissä rajoituksille. Heti kun kaikki annetun LPP:n epäyhtälöt on piirretty XY-kaavioon, kaikkien epäyhtälöiden yhteinen alue antaa optimaalisen ratkaisun. Kaikki mahdollisen alueen kulmapisteet lasketaan ja tavoitefunktion arvo kaikissa näissä pisteissä lasketaan, sitten näitä arvoja vertaamalla saadaan LPP:n optimaalinen ratkaisu.
Esimerkki: Etsi z = 6x + 9y maksimi- ja minimiarvo, kun rajoitusehdot ovat,
- 2x + 3v ≤ 12
- x ja y ≥ 0
- x + y ≤ 5
Ratkaisu:
Vaihe 1 : Muunna ensin yhtälöt normaaliyhtälöiksi. Näin ollen yhtälöt ovat 2x+3y = 0, x = 0, y = 0 ja x + y = 5.
Vaihe 2 : Etsi pisteet, joissa 2x + 3y ja x + y = 5 leikkaavat x-akselin ja y-akselin. Löytääksesi x-akselin leikkauspisteen, laita y = 0 vastaavaan yhtälöön ja etsi piste. Samoin y-akselin leikkauspisteille laita x = 0 vastaavaan yhtälöön.
Vaihe 3 : Piirrä kaksi viivaa, jotka leikkaavat x-akselin ja y-akselin. Havaitsemme, että kaksi akselia leikkaavat toisensa kohdassa (3,2).
Vaihe 4 : Kun x ≥ 0 ja y ≥ 0, havaitsemme, että molempia yhtälöjä noudatetaan. Siten alue sisältää alueen, jota ympäröi kaksi akselia ja molempia linjoja, mukaan lukien origo. Piirretty alue on esitetty alla kuvassa.
Vaihe 5 : Etsi Z jokaiselle pisteelle ja maksimille ja minimille.
Koordinaatit Z = 6x + 9v (0,5) Z = 45 (0,4) Z = 36 (5.0) Z = 30 (6.0) Z = 36 (3.2) Z = 36 Näin ollen havaitsemme, että Z = 6x + 9y on maksimi kohdassa (0,5) ja minimi kohdassa (5,0).
Lineaariset ohjelmointisovellukset
Lineaarisella ohjelmoinnilla on sovelluksia useilla aloilla. Sitä käytetään prosessin vähimmäiskustannusten löytämiseen, kun kaikki ongelmien rajoitteet on annettu. Sitä käytetään optimoimaan ajoneuvon kuljetuskustannukset jne. Lineaarisen ohjelmoinnin eri sovelluksia ovat
Engineering Industries
Engineering Industries käyttää lineaarista ohjelmointia ratkaistakseen suunnittelu- ja valmistusongelmia ja saadakseen maksimaalisen tuoton tietystä tilasta.
Teollisuusteollisuus
Manufacturing Industries käyttää lineaarista ohjelmointia maksimoidakseen yritysten voiton ja alentaakseen valmistuskustannuksia.
Energiateollisuus
Energiayhtiöt käyttävät lineaarista ohjelmointia tuotantonsa optimoimiseksi.
Liikenneteollisuus
Lineaarista ohjelmointia käytetään myös kuljetusteollisuudessa etsimään polkua kuljetuskustannusten minimoimiseksi.
Lineaarisen ohjelmoinnin merkitys
Lineaarisella ohjelmoinnilla on valtava merkitys eri toimialoilla, sillä se maksimoi tuotosarvon ja minimoi syöttöarvot erilaisten rajoitusten mukaan.
LP on erittäin käyttökelpoinen, kun ongelman ratkaisemisessa on useita ehtoja ja meidän on optimoitava ongelman tulos, eli joko meidän on löydettävä minimi- tai maksimiarvo tietyn ehdon mukaan.
Lue lisää,
- Lineaariset epäyhtälöt
- Lineaaristen epäyhtälöiden algebrallinen ratkaisu
Lineaarisen ohjelmoinnin ongelmat
Ongelma 1: Yritys valmistaa ja myy kahdentyyppisiä tuotteita, ja kunkin yksikön a ja b tuotantokustannukset ovat 200 rupiaa ja 150 rupiaa, kukin tuoteyksikkö tuottaa 20 rupiaa ja jokainen tuote b yksikkö tuottaa 15 rupiaa myytäessä. . Yhtiö arvioi A:n ja B:n kuukausikysynnän olevan korkeintaan korjatun yksikön rajoissa koko kuukauden tuotantobudjetissa on 50 000 rupiaa. Kuinka monta yksikköä yrityksen tulee valmistaa saadakseen maksimivoiton kuukausittaisesta myynnistään ja b?
Ratkaisu:
Olkoon x = A-tyypin yksiköiden lukumäärä
y = B-tyypin yksiköiden lukumäärä
Maksimoi Z = 40x + 50v
Rajoitusten mukaan
3x + y ≤ 9
x + 2y ≤ 8
ja x, y ≥ 0
Harkitse yhtälöä,
3x + y = 9
x = 3
y = 0
ja x + 2y = 8
x = 8
y = 0
Nyt voimme määrittää Z:n maksimiarvon arvioimalla Z:n arvon neljässä pisteessä (pisteessä) on esitetty alla.
Vertices
Z = 40x + 50 v
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Suurin voitto, Z = Rs. 230
∴ A-tyypin yksiköiden lukumäärä on 2 ja tyypin B yksiköiden lukumäärä on 3.
Tehtävä 2: Maksimoi Z = 3x + 4y.
Rajoituksista riippuen x + y ≤ 450, 2x + y ≤ 600 ja x, y ≤ 0.
Ratkaisu:
Meillä on annettu
Rajoitukset (1)
X + Y = 450
Laitetaan x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Laitetaan y = 0, ⇒ x + 0 = 450 ⇒ x = 450
alkaen, Rajoitukset (2)
2x + y = 600
Laitetaan x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Laitetaan y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Nyt meillä on pistekoordinaatit Z = 3x + 4y
| Vertices | Z = 3x + 4v |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300 + 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 merkkijono char javaan |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Siksi optimaalinen ratkaisumaksimi Z = 1800 koordinaatilla x = 0 ja y = 450. Kaavio on esitetty alla.

Lineaarisen ohjelmoinnin ajantasaiset sovellukset
Lineaarista ohjelmointia, tehokasta matemaattista tekniikkaa, käytetään optimointiongelmien ratkaisemiseen eri toimialoilla. Tässä on joitain nykyaikaisia sovelluksia:
- Toimitusketjun optimointi : Lineaarinen ohjelmointi auttaa yrityksiä minimoimaan kustannukset ja maksimoimaan toimitusketjunsa tehokkuuden. Sitä käytetään kustannustehokkaimpien kuljetusreittien, varastotoimintojen ja varastonhallintastrategioiden määrittämiseen.
- Energian hallinta : Energia-alalla käytetään lineaarista ohjelmointia energiantuotantomenetelmien yhdistelmän optimointiin. Tähän sisältyy perinteisten energialähteiden ja uusiutuvien energialähteiden tasapainottaminen kustannusten ja ympäristövaikutusten vähentämiseksi samalla kun kysyntä vastataan.
- Tietoliikenneverkkojen suunnittelu : Lineaarinen ohjelmointi auttaa tehokkaiden tietoliikenneverkkojen suunnittelussa. Se auttaa varaamaan kaistanleveyttä, suunnittelemaan verkkoasetelmia ja optimoimaan tietovirran nopean tiedonsiirron varmistamiseksi pienemmillä kustannuksilla.
- Taloussuunnittelu : Yritykset ja talousanalyytikot käyttävät lineaarista ohjelmointia salkun optimointiin, riskienhallintaan ja pääomabudjetointiin. Se auttaa tekemään sijoituspäätöksiä, jotka maksimoivat tuoton ja minimoivat riskin.
- Terveydenhuollon logistiikka : Terveydenhuollossa lineaarista ohjelmointia käytetään optimoimaan resurssien, kuten sairaalasänkyjen, hoitohenkilökunnan ja laitteiden, allokointi. Se on ratkaisevan tärkeää potilaiden hoidon parantamisen, odotusaikojen lyhentämisen ja kustannusten tehokkaan hallinnan kannalta.
- Valmistusprosessin optimointi : Lineaarista ohjelmointia käytetään määrittämään optimaaliset tuotantotasot useille tuotteille tuotantolaitoksessa ottaen huomioon rajoitukset, kuten työvoiman, materiaalien ja koneiden saatavuuden.
- Maatalouden suunnittelu : Maanviljelijät ja maataloussuunnittelijat käyttävät lineaarista ohjelmointia päättääkseen viljelykasvien valinnasta, maankäytöstä ja resurssien allokoinnista sadon ja voiton maksimoimiseksi resursseja säästäen.
- Lentoyhtiön miehistön aikataulut : Lentoyhtiöt käyttävät lineaarista ohjelmointia aikatauluttaakseen miehistöt tehokkaasti, varmistaen, että lennoilla on määräysten mukainen henkilökunta ja minimoiden toimintakustannukset.
Nämä sovellukset osoittavat lineaarisen ohjelmoinnin monipuolisuuden ja tehon monimutkaisten optimointiongelmien ratkaisemisessa eri sektoreilla ja osoittavat sen merkityksen nykypäivän datalähtöisessä maailmassa.
Lineaarinen ohjelmointi operaatiotutkimuksessa
- Ydintyökalu : Lineaarinen ohjelmointi on perustyökalu operaatiotutkimuksessa resurssien optimointiin.
- Päätöksenteko : Auttaa tekemään parhaat päätökset resurssien allokoinnista, voittojen maksimoinnista tai kustannusten minimoimisesta.
- Laajat sovellukset : Käytetään useilla aloilla, kuten logistiikassa, valmistuksessa, rahoituksessa ja terveydenhuollossa monimutkaisten ongelmien ratkaisemiseen.
- Tosimaailman ongelmien mallintaminen : Muuntaa reaalimaailman ongelmat matemaattisiksi malleiksi löytääkseen tehokkaimmat ratkaisut.
Yksinkertainen menetelmä
- Optimointialgoritmi : Simplex-menetelmä on tehokas algoritmi, jota käytetään lineaarisessa ohjelmoinnissa optimaalisen ratkaisun löytämiseksi lineaarisille epäyhtälöille.
- Vaiheittainen lähestymistapa : Se etenee iteratiivisesti kohti parasta ratkaisua navigoimalla rajoitusten määrittelemän mahdollisen alueen reunoja.
- Tehokkuus : Tunnettu tehokkuudestaan suurten lineaaristen ohjelmointiongelmien ratkaisemisessa.
- Monipuolisuus : Sovellettavissa useilla aloilla, kuten ruokavalion suunnittelussa, verkkovirrassa, tuotannon ajoituksessa ja muissa, mikä osoittaa sen monipuolisuuden.
Lineaarinen ohjelmointi – UKK
Mitä on lineaarinen ohjelmointi?
Lineaarinen ohjelmointi on matemaattinen käsite, jota käytetään tietyn lineaarisen ongelman optimointiin, jolla on useita rajoituksia. Lineaarista ohjelmointia käyttämällä saadaan annetun ongelman optimaalinen tulos
Mitä ovat lineaarisen ohjelmoinnin ongelmat?
Lineaariset ohjelmointiongelmat (LPP) ovat ongelmia, jotka antavat optimaalisen ratkaisun annettuihin olosuhteisiin.
Mikä on lineaarinen ohjelmointikaava?
Yleiset lineaariset ohjelmointikaavat ovat
- Tavoitefunktio: Z = ax + by
- Rajoitukset: px + qy ≤ r, sx + ty ≤ u
- Ei-negatiiviset rajoitukset: x ≥ 0, y ≥ 0
Mitä erilaisia lineaariohjelmointityyppejä on?
Erilaisia lineaarisia ohjelmointimenetelmiä ovat mm.
- Lineaarinen ohjelmointi Simplex-menetelmällä
- Lineaarinen ohjelmointi R-menetelmällä
- Lineaarinen ohjelmointi graafisella menetelmällä
Mitkä ovat lineaarisen ohjelmoinnin vaatimukset?
Lineaaristen ohjelmointiongelmien erilaiset vaatimukset ovat,
- Lineaarisuus
- Objektiivinen toiminto
- Rajoitukset
- Ei-negatiivisuus
Mitkä ovat lineaarisen ohjelmoinnin edut?
Lineaarisen ohjelmoinnin monia etuja ovat mm.
- Se tarjoaa optimaalisen ratkaisun mihin tahansa lineaariseen ongelmaan.
- Se on helppokäyttöinen ja antaa aina tasaisen tuloksen
- Se auttaa maksimoimaan voiton ja alentamaan tuotantokustannuksia.