Lineaarinen regressio ja logistinen regressio ovat kaksi kuuluisaa koneoppimisalgoritmia, jotka kuuluvat valvotun oppimistekniikan piiriin. Koska molemmat algoritmit ovat luonteeltaan valvottuja, nämä algoritmit käyttävät merkittyä tietojoukkoa ennusteiden tekemiseen. Mutta tärkein ero niiden välillä on se, miten niitä käytetään. Lineaarista regressiota käytetään regressioongelmien ratkaisemiseen, kun taas logistista regressiota käytetään luokitusongelmien ratkaisemiseen. Molempien algoritmien kuvaus on annettu alla yhdessä erotaulukon kanssa.
Lineaarinen regressio:
- Lineaarinen regressio on yksi yksinkertaisimmista koneoppimisalgoritmeista, joka kuuluu valvotun oppimisen tekniikkaan ja jota käytetään regressioongelmien ratkaisemiseen.
- Sitä käytetään jatkuvan riippuvan muuttujan ennustamiseen riippumattomien muuttujien avulla.
- Lineaarisen regression tavoitteena on löytää paras sovitusviiva, joka voi ennustaa tarkasti jatkuvan riippuvan muuttujan ulostulon.
- Jos ennustamiseen käytetään yhtä riippumatonta muuttujaa, sitä kutsutaan yksinkertaiseksi lineaariseksi regressioksi ja jos riippumattomia muuttujia on enemmän kuin kaksi, niin tällaista regressiota kutsutaan moninkertaiseksi lineaariksi regressioksi.
- Löytämällä parhaan sovitusviivan algoritmi määrittää riippuvan muuttujan ja riippumattoman muuttujan välisen suhteen. Ja suhteen tulee olla luonteeltaan lineaarinen.
- Lineaarisen regression tulosten tulee olla vain jatkuvia arvoja, kuten hinta, ikä, palkka jne. Riippuvaisen muuttujan ja riippumattoman muuttujan välinen suhde voidaan näyttää alla olevassa kuvassa:

Yllä olevassa kuvassa riippuva muuttuja on Y-akselilla (palkka) ja riippumaton muuttuja on x-akselilla (kokemus). Regressioviiva voidaan kirjoittaa seuraavasti:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Missä0ja a1ovat kertoimet ja ε on virhetermi.
Logistinen regressio:
- Logistinen regressio on yksi suosituimmista koneoppimisalgoritmeista, joka kuuluu valvotun oppimisen tekniikoihin.
- Sitä voidaan käyttää sekä luokittelu- että regressio-ongelmiin, mutta pääasiassa luokitusongelmiin.
- Logistista regressiota käytetään kategorisen riippuvan muuttujan ennustamiseen riippumattomien muuttujien avulla.
- Logistisen regression ongelman tulos voi olla vain välillä 0 ja 1.
- Logistista regressiota voidaan käyttää, kun vaaditaan kahden luokan välinen todennäköisyys. Esimerkiksi sataako tänään vai ei, joko 0 tai 1, tosi vai taru jne.
- Logistinen regressio perustuu Maximum Likelihood -arvioinnin käsitteeseen. Tämän arvion mukaan havaitun datan pitäisi olla todennäköisin.
- Logistisessa regressiossa syötteiden painotettu summa välitetään aktivointifunktion läpi, joka voi kartoittaa arvot välillä 0 ja 1. Tällainen aktivointifunktio tunnetaan nimellä sigmoiditoiminto ja saatua käyrää kutsutaan sigmoidikäyräksi tai S-käyräksi. Harkitse alla olevaa kuvaa:

- Logistisen regression yhtälö on:

Ero lineaarisen regression ja logistisen regression välillä:
| Lineaarinen regressio | Logistinen regressio |
|---|---|
| Lineaarista regressiota käytetään jatkuvan riippuvan muuttujan ennustamiseen käyttämällä annettua riippumattomien muuttujien joukkoa. | Logistista regressiota käytetään kategorisen riippuvan muuttujan ennustamiseen käyttämällä annettua riippumattomien muuttujien joukkoa. |
| Lineaarista regressiota käytetään regressio-ongelman ratkaisemiseen. | Logistista regressiota käytetään luokitusongelmien ratkaisemiseen. |
| Lineaarisessa regressiossa ennustamme jatkuvien muuttujien arvon. | Logistisessa regressiossa ennustamme kategoristen muuttujien arvot. |
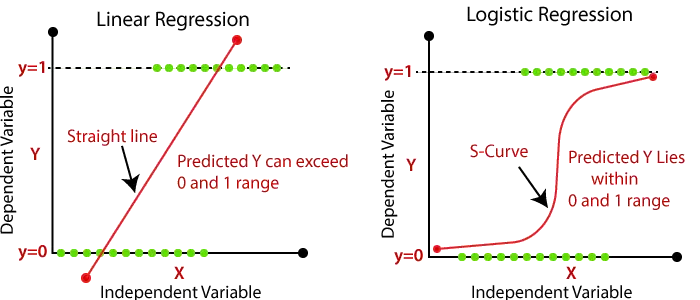
| Lineaarisessa regressiossa löydämme parhaan sovitusviivan, jonka avulla voimme helposti ennustaa ulostulon. | Logistic Regressionissa löydämme S-käyrän, jonka avulla voimme luokitella näytteet. |
| Tarkkuuden estimointiin käytetään pienimmän neliön estimointimenetelmää. | Tarkkuuden estimointiin käytetään maksimitodennäköisyyden estimointimenetelmää. |
| Lineaarisen regression tulosteen on oltava jatkuva arvo, kuten hinta, ikä jne. | Logistic Regression -tuloksen on oltava kategoriallinen arvo, kuten 0 tai 1, Kyllä tai ei jne. |
| Lineaarisessa regressiossa edellytetään, että riippuvan muuttujan ja riippumattoman muuttujan välisen suhteen on oltava lineaarinen. | Logistisessa regressiossa ei vaadita riippuvan ja riippumattoman muuttujan välistä lineaarista suhdetta. |
| Lineaarisessa regressiossa riippumattomien muuttujien välillä voi olla kollineaarisuutta. | Logistisessa regressiossa riippumattoman muuttujan välillä ei pitäisi olla kollineaarisuutta. |
