Logistinen regressio R-ohjelmoinnissa on luokitusalgoritmi, jota käytetään tapahtuman onnistumisen ja epäonnistumisen todennäköisyyksien selvittämiseen. Logistista regressiota käytetään, kun riippuva muuttuja on luonteeltaan binäärinen (0/1, tosi/epätosi, kyllä/ei). Logit-funktiota käytetään linkkifunktiona binomijakaumassa.
Binääritulosmuuttujan todennäköisyys voidaan ennustaa käyttämällä tilastollista mallinnustekniikkaa, joka tunnetaan nimellä logistinen regressio. Sitä käytetään laajasti monilla eri aloilla, mukaan lukien markkinointi, rahoitus, yhteiskuntatieteet ja lääketieteellinen tutkimus.
Logistinen funktio, jota yleisesti kutsutaan sigmoidifunktioksi, on logistisen regression taustalla oleva perusidea. Tätä sigmoidifunktiota käytetään logistisessa regressiossa kuvaamaan korrelaatiota ennustajamuuttujien ja binäärituloksen todennäköisyyden välillä.

Logistinen regressio R-ohjelmoinnissa
Logistinen regressio tunnetaan myös nimellä Binomiaalinen logistinen regressio . Se perustuu sigmoidifunktioon, jossa lähtö on todennäköisyys ja tulo voi olla -äärettömästä + äärettömään.
Teoria
Logistinen regressio tunnetaan myös yleisenä lineaarisena mallina. Koska sitä käytetään luokittelutekniikkana laadullisen vasteen ennustamiseen, y:n arvo vaihtelee välillä 0-1 ja se voidaan esittää seuraavalla yhtälöllä:

Logistinen regressio R-ohjelmoinnissa
s on kiinnostavan ominaisuuden todennäköisyys. Todennäköisyyssuhde määritellään onnistumisen todennäköisyydeksi verrattuna epäonnistumisen todennäköisyyteen. Se on logististen regressiokertoimien avainesitys, ja se voi ottaa arvoja välillä 0 ja ääretön. Todennäköisyyssuhde on 1, kun onnistumisen todennäköisyys on yhtä suuri kuin epäonnistumisen todennäköisyys. Todennäköisyyssuhde 2 on, kun onnistumisen todennäköisyys on kaksi kertaa epäonnistumisen todennäköisyys. Todennäköisyyssuhde 0,5 on, kun epäonnistumisen todennäköisyys on kaksi kertaa onnistumisen todennäköisyys.
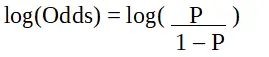
Logistinen regressio R-ohjelmoinnissa
Koska työskentelemme binomiaalisen jakauman (riippuvaisen muuttujan) kanssa, meidän on valittava linkkifunktio, joka sopii parhaiten tähän jakaumaan.
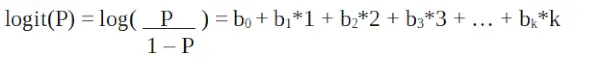
Logistinen regressio R-ohjelmoinnissa
Se on a logit-toiminto . Yllä olevassa yhtälössä sulut valitaan maksimoimaan näytearvojen havainnoinnin todennäköisyys sen sijaan, että minimoidaan neliövirheiden summa (kuten tavallinen regressio). Logit tunnetaan myös kertoimien lokina. Logit-funktion on oltava lineaarisesti suhteessa riippumattomiin muuttujiin. Tämä on yhtälöstä A, jossa vasen puoli on x:n lineaarinen yhdistelmä. Tämä on samanlainen kuin OLS-oletus, että y liittyy lineaarisesti x:ään. Muuttujat b0, b1, b2 … jne. ovat tuntemattomia ja ne on arvioitava käytettävissä olevien harjoitustietojen perusteella. Logistisessa regressiomallissa b1:n kertominen yhdellä yksiköllä muuttaa logitin b0:lla. Yhden yksikön muutoksesta johtuvat P-muutokset riippuvat kerrotusta arvosta. Jos b1 on positiivinen, P kasvaa ja jos b1 on negatiivinen, P pienenee.
Tietojoukko
mtcars (moottoritrendiautojen tietesti) sisältää polttoaineen kulutuksen, suorituskyvyn ja 10 auton suunnittelun näkökohtaa 32 autolle. Se tulee esiasennettuna dplyr paketti R:ssä.
R
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
>
int parseint
Logistisen regression suorittaminen tietojoukolle
Logistinen regressio toteutetaan R:ssä käyttäen glm() harjoittelemalla mallia käyttämällä tietojoukon ominaisuuksia tai muuttujia.
R
c-ohjelma kaksiulotteiselle taulukolle
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Tietojen jakaminen
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Lähtö:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Leikkaus) 1,58781 2,60087 0,610 0,5415 paino 1,36958 1,60524 0,853 0,3936 näyttö -0,02969 0,01577 -1,8588 0,0. --- Signif. koodit: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Binomiperheen dispersioparametri on 1) Nollapoikkeama: 34,617 24 vapausasteella Jäännöspoikkeama: 20.21 22 vapausastetta AIC: 26.212 Fisher Scoring iteraatioiden lukumäärä: 6>
- Kutsu: Logistiseen regressiomalliin sopiva funktiokutsu näytetään sekä tiedot perheestä, kaavasta ja tiedoista. Poikkeamien jäännösarvot: Nämä ovat poikkeamajäännöksiä, jotka mittaavat mallin sopivuusastetta. Ne tarkoittavat eroja todellisten vastausten ja logistisen regressiomallin ennustaman todennäköisyyden välillä. Kertoimet: Nämä kertoimet logistisessa regressiossa edustavat vastemuuttujan log odds tai logit. Arvioituihin kertoimiin liittyvät keskivirheet on esitetty standardissa. Virhesarake. Merkityskoodit: Kunkin ennustajamuuttujan merkitsevyystaso ilmaistaan merkitsevyyskoodeilla. Dispersioparametri: Logistisessa regressiossa dispersioparametri toimii binomijakauman skaalausparametrina. Se on asetettu arvoon 1 tässä tapauksessa, mikä osoittaa, että oletettu hajonta on 1. Nollapoikkeama: Nollapoikkeama laskee mallin poikkeaman, kun vain leikkauspiste otetaan huomioon. Se symboloi poikkeamaa, joka seuraisi mallista, jossa ei ole ennustajia. Jäännöspoikkeama: Jäännöspoikkeama laskee mallin poikkeaman ennustajien sovituksen jälkeen. Se tarkoittaa jäännöspoikkeamaa ennustajien huomioimisen jälkeen. AIC: Akaike Information Criterion (AIC), joka ottaa huomioon ennustajien määrän, on mallin sopivuuden mittari. Se rankaisee monimutkaisempia malleja liiallisen sovituksen estämiseksi. Paremmin istuvat mallit ilmaistaan pienemmillä AIC-arvoilla. Fisher Scoring -iteraatioiden määrä: Fisher-pisteytysmenettelyn tarvitsemien iteraatioiden määrä mallin parametrien arvioimiseksi ilmaistaan iteraatioiden lukumäärällä.
Ennusta testitiedot mallin perusteella
R
pawandeep rajan
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Lähtö:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Lähtö:
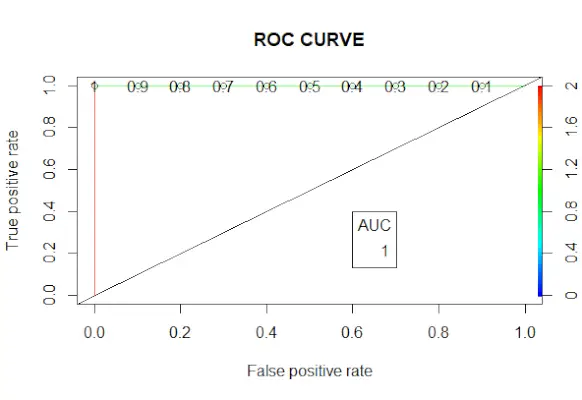
ROC-käyrä
Esimerkki 2:
Voimme suorittaa logistisen regressiomallin Titanic Dataset R:ssä.
R
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Lähtö:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Siirto) 4.022e-16 8.660e-01 0 1 Luokka 2. -9.762e-16 1.000e+00 0 1 Luokka 3 -4.699e-16 1.000e+00 0 1 ClassCrew -5.551.0-1.651. 00 0 1 SukupuoliNainen -3.140e-16 7.071e-01 0 1 IkäAikuinen 5.103e-16 7.071e-01 0 1 (Dispergointiparametri binomiaaliperheelle otetaan 1) Nollapoikkeama: 44.1361 vapausaste 4.4:4. 26 vapausasteessa AIC: 56.361 Fisher Scoring iteraatioiden määrä: 2>
Piirrä ROC-käyrä Titanicin datajoukolle
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
instantoitu java
>
>
Lähtö:
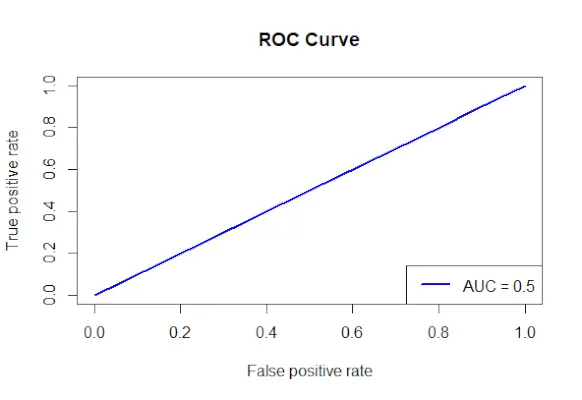
ROC-käyrä
- Selviytyneiden ennustamiseen käytetyt tekijät määritellään, ja kaavaa Survived Class + Sukupuoli + Ikä käytetään logistisen regressiomallin luomiseen.
- Käyttämällä ennustaa()-funktiota ennusteet tehdään tietojoukolle sovitetun mallin avulla.
- Ennustetut todennäköisyydet yhdistetään todellisten tulosarvojen kanssa ennusteobjektin rakentamiseksi käyttämällä ROCR-paketin ennustus()-menetelmää.
- Todellisen positiivisen nopeuden (tpr) mitta ja väärän positiivisen nopeuden x-akselin mitta (fpr) määritetään, ja ROC-käyräobjekti luodaan käyttämällä performance()-funktiota ROCR-paketista.
- ROC-käyräobjekti (roc_obj), joka määrittää pääotsikon, värin ja viivan leveyden, piirretään plot()-funktiolla.
- Se käyttää performance()-funktiota, jossa mitta = auc määrittää AUC-arvon (area under the curve) ja lisää kaavioon tunnisteet ja selitteen.
