ALIN YHTEINEN ESI-ISÄ BINÄÄRIPUUSSA - TECHCODEVIEW.COM

Mikä on alin yhteinen esi-isä binääripuussa?

The alin yhteinen esi-isä on puun alin solmu, jolla on sekä n1 että n2 as jälkeläiset, missä n1 ja n2 ovat solmut, joille haluamme löytää LCA:n. Näin ollen binääripuun, jossa on solmut n1 ja n2, LCA on n1:n ja n2:n yhteinen esi-isä, joka sijaitsee kauimpana juuresta.

Lowest Common Ancestor (LCA) -sovellus:

Puun solmuparien välisen etäisyyden määrittäminen: etäisyys n1:stä n2:een voidaan laskea etäisyydeksi juuresta n1:een plus etäisyys juuresta n2:een, miinus kaksinkertainen etäisyys juuresta niiden alimpaan yhteiseen. esi-isä.

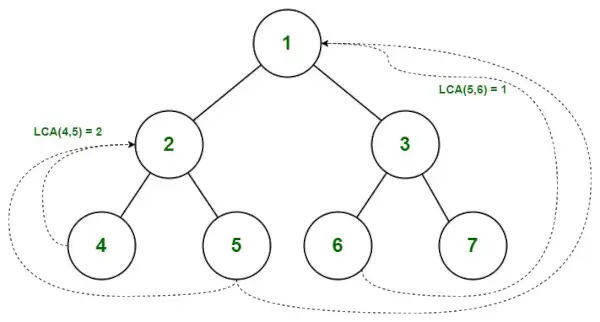
Binääripuun alin yhteinen esi-isä

Suositeltu käytäntö Alin yhteinen esi-isä binääripuussa Kokeile!

Alin yhteinen esi-isä binääripuussa tallentamalla polut juuresta n1:een ja juuresta n2:een:

Tämän lähestymistavan ideana on tallentaa polku juuresta n1:een ja juuresta n2:een kahteen erilliseen tietorakenteeseen. Tarkastele sitten samanaikaisesti tietorakenteeseen tallennettuja arvoja ja etsi ensimmäinen ristiriita.

Kuva:

Etsi LCA arvoista 5 ja 6

Polku juuresta 5:een = { 1, 2, 5 }
Polku juuresta 6:een = { 1, 3, 6 }

Aloitamme tarkistamisen indeksistä 0. Koska molemmat arvot täsmäävät (polkuA[0] = polkuB[0]), siirrymme seuraavaan indeksiin.

polkuA[1] ei ole sama kuin polkuB[1], siinä on epäsuhta, joten otamme huomioon edellisen arvon.

Siksi (5,6) LCA = 1

Ratkaise ongelma noudattamalla alla olevia ohjeita:

Etsi polku juuresta n1:een ja tallenna se vektoriin tai taulukkoon.
Etsi polku juuresta n2:een ja tallenna se toiseen vektoriin tai taulukkoon.
Kulje molempia polkuja, kunnes taulukoiden arvot ovat samat. Palauta yhteinen elementti juuri ennen yhteensopimattomuutta.

Seuraavassa on yllä olevan algoritmin toteutus:

C++

// C++ Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> #include> using> namespace> std;> // A Binary Tree node> struct> Node {> >int> key;> >struct> Node *left, *right;> };> // Utility function creates a new binary tree node with> // given key> Node* newNode(>int> k)> {> >Node* temp =>new> Node;> >temp->avain = k;> >temp->vasen = temp->right = NULL;> >return> temp;> }> // Finds the path from root node to given root of the tree,> // Stores the path in a vector path[], returns true if path> // exists otherwise false> bool> findPath(Node* root, vector<>int>>& polku,>int> k)> (root->right && findPath(juuri->oikea, polku, k)))> >return> true>;> >// If not present in subtree rooted with root, remove> >// root from path[] and return false> >path.pop_back();> >return> false>;> > // Returns LCA if node n1, n2 are present in the given> // binary tree, otherwise return -1> int> findLCA(Node* root,>int> n1,>int> n2)> > // Driver program to test above functions> int> main()> {> >// Let us create the Binary Tree shown in above diagram.> >Node* root = newNode(1);> >root->vasen = newNode(2);> >root->oikea = newNode(3);> >root->vasen->vasen = uusiSolmu(4);> >root->vasen->oikea = newNode(5);> >root->oikea->vasen = uusiSolmu(6);> >root->oikea->oikea = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5);> >cout <<>

'
LCA(4, 6) = '>

<< findLCA(root, 4, 6);> >cout <<>

'
LCA(3, 4) = '>

<< findLCA(root, 3, 4);> >cout <<>

'
LCA(2, 4) = '>

<< findLCA(root, 2, 4);> >return> 0;> }>

Java

// Java Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA of> // two given values n1 and n2> import> java.util.ArrayList;> import> java.util.List;> // A Binary Tree node> class> Node {> >int> data;> >Node left, right;> >Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> List path1 =>new> ArrayList();> >private> List path2 =>new> ArrayList();> >// Finds the path from root node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.clear();> >path2.clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >System.out.println((path1.size()>>>)> >?>'n1 is present'> >:>'n1 is missing'>);> >System.out.println((path2.size()>>>)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> ->1>;> >}> >int> i;> >for> (i =>0>

; i   i++) {  // System.out.println(path1.get(i) + ' ' +  // path2.get(i));  if (!path1.get(i).equals(path2.get(i)))  break;  }  return path1.get(i - 1);  }  // Finds the path from root node to given root of the  // tree, Stores the path in a vector path[], returns  // true if path exists otherwise false  private boolean findPath(Node root, int n,  List path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node will be removed if  // not in path from root to n.  path.add(root.data);  if (root.data == n ||  findPath(root.left, n, path) ||  findPath(root.right, n, path)) {  return true;  }  // If not present in subtree rooted with root,  // remove root from path[] and return false  path.remove(path.size() - 1);  return false;  }  // Driver code  public static void main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  System.out.println('LCA(4, 5) = '  + tree.findLCA(4, 5));  System.out.println('LCA(4, 6) = '  + tree.findLCA(4, 6));  System.out.println('LCA(3, 4) = '  + tree.findLCA(3, 4));  System.out.println('LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Sreenivasulu Rayanki.>

Python 3

# Python Program for Lowest Common Ancestor in a Binary Tree> # O(n) solution to find LCS of two given values n1 and n2> # A binary tree node> class> Node:> ># Constructor to create a new binary node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # Finds the path from root node to given root of the tree.> # Stores the path in a list path[], returns true if path> # exists otherwise false> def> findPath(root, path, k):> ># Baes Case> >if> root>is> None>:> >return> False> ># Store this node is path vector. The node will be> ># removed if not in path from root to k> >path.append(root.key)> ># See if the k is same as root's key> >if> root.key>=>=> k:> >return> True> ># Check if k is found in left or right sub-tree> >if> ((root.left !>=> None> and> findPath(root.left, path, k))>or> >(root.right !>=> None> and> findPath(root.right, path, k))):> >return> True> ># If not present in subtree rooted with root, remove> ># root from path and return False> >path.pop()> >return> False> # Returns LCA if node n1 , n2 are present in the given> # binary tree otherwise return -1> def> findLCA(root, n1, n2):> ># To store paths to n1 and n2 fromthe root> >path1>=> []> >path2>=> []> ># Find paths from root to n1 and root to n2.> ># If either n1 or n2 is not present , return -1> >if> (>not> findPath(root, path1, n1)>or> not> findPath(root, path2, n2)):> >return> ->1> ># Compare the paths to get the first different value> >i>=> 0> >while>(i <>len>(path1)>and> i <>len>(path2)):> >if> path1[i] !>=> path2[i]:> >break> >i>+>=> 1> >return> path1[i>->1>]> # Driver program to test above function> if> __name__>=>=> '__main__'>:> > ># Let's create the Binary Tree shown in above diagram> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> > >print>(>'LCA(4, 5) = %d'> %> (findLCA(root,>4>,>5>,)))> >print>(>'LCA(4, 6) = %d'> %> (findLCA(root,>4>,>6>)))> >print>(>'LCA(3, 4) = %d'> %> (findLCA(root,>3>,>4>)))> >print>(>'LCA(2, 4) = %d'> %> (findLCA(root,>2>,>4>)))> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# Program for Lowest Common> // Ancestor in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> using> System.Collections;> using> System;> // A Binary Tree node> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> ArrayList path1 =>new> ArrayList();> >private> ArrayList path2 =>new> ArrayList();> >// Finds the path from root> >// node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.Clear();> >path2.Clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >Console.Write((path1.Count>0)> >?>'n1 is present'> >:>'n1 is missing'>);> >Console.Write((path2.Count>0)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> -1;> >}> >int> i;> >for>

(i = 0; i   i++) {  // System.out.println(path1.get(i)  // + ' ' + path2.get(i));  if ((int)path1[i] != (int)path2[i])  break;  }  return (int)path1[i - 1];  }  // Finds the path from root node  // to given root of the tree,  // Stores the path in a vector  // path[], returns true if path  // exists otherwise false  private bool findPath(Node root, int n, ArrayList path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node  // will be removed if not in  // path from root to n.  path.Add(root.data);  if (root.data == n) {  return true;  }  if (root.left != null  && findPath(root.left, n, path)) {  return true;  }  if (root.right != null  && findPath(root.right, n, path)) {  return true;  }  // If not present in subtree  // rooted with root, remove root  // from path[] and return false  path.RemoveAt(path.Count - 1);  return false;  }  // Driver code  public static void Main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  Console.Write('LCA(4, 5) = ' + tree.findLCA(4, 5));  Console.Write('
LCA(4, 6) = '  + tree.findLCA(4, 6));  Console.Write('
LCA(3, 4) = '  + tree.findLCA(3, 4));  Console.Write('
LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Rutvik_56>

Javascript

> >// JavaScript Program for Lowest Common> >// Ancestor in a Binary Tree> >// A O(n) solution to find LCA of> >// two given values n1 and n2> > >class Node> >{> >constructor(value) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = value;> >}> >}> > >let root;> >let path1 = [];> >let path2 = [];> > >// Finds the path from root node to given root of the tree.> >function> findLCA(n1, n2) {> >path1 = [];> >path2 = [];> >return> findLCAInternal(root, n1, n2);> >}> > >function> findLCAInternal(root, n1, n2) {> > >if> (!findPath(root, n1, path1) || !findPath(root, n2, path2))> >{> >document.write((path1.length>0) ?>> 'n1 is present'> :>'n1 is missing'>);> >document.write((path2.length>0) ?>> 'n2 is present'> :>'n2 is missing'>);> >return> -1;> >}> > >let i;> >for>

(i = 0; i     // System.out.println(path1.get(i) + ' ' + path2.get(i));  if (path1[i] != path2[i])  break;  }    return path1[i-1];  }    // Finds the path from root node to   // given root of the tree, Stores the  // path in a vector path[], returns true  // if path exists otherwise false  function findPath(root, n, path)  {  // base case  if (root == null) {  return false;  }    // Store this node . The node will be removed if  // not in path from root to n.  path.push(root.data);    if (root.data == n) {  return true;  }    if (root.left != null && findPath(root.left, n, path)) {  return true;  }    if (root.right != null && findPath(root.right, n, path)) {  return true;  }    // If not present in subtree rooted with root,   // remove root from  // path[] and return false  path.pop();    return false;  }    root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.left.left = new Node(4);  root.left.right = new Node(5);  root.right.left = new Node(6);  root.right.right = new Node(7);  document.write('LCA(4, 5) = ' + findLCA(4,5) + '');  document.write('LCA(4, 6) = ' + findLCA(4,6) + '');  document.write('LCA(3, 4) = ' + findLCA(3,4) + '');  document.write('LCA(2, 4) = ' + findLCA(2,4));>

Lähtö

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Aika monimutkaisuus: PÄÄLLÄ). Puu ajetaan kahdesti ja sitten polkutaulukoita verrataan.
Aputila: PÄÄLLÄ). Lisätilaa polulle 1 ja polku2.

Alin yhteinen esi-isä binääripuussa kertakierroksella:

Ajatuksena on kulkea puun poikki juuresta alkaen. Jos jokin annetuista avaimista (n1 ja n2) vastaa juuria, juuri on LCA (olettaen, että molemmat avaimet ovat läsnä). Jos juuri ei täsmää minkään avaimen kanssa, toistetaan vasemmalle ja oikealle alipuulle.

Solmu, jonka vasemmassa alipuussa on yksi avain ja oikea alipuussa toinen avain, on LCA.

Jos molemmat näppäimet ovat vasemmassa alipuussa, myös vasemmalla alipuulla on LCA,

Muussa tapauksessa LCA on oikeassa alipuussa.

Kuva:

Etsi LCA arvoista 5 ja 6

Juuri osoittaa solmuun, jonka arvo on 1, koska sen arvo ei vastaa arvoa { 5, 6 }. Etsimme avainta vasemmasta alipuusta ja oikeasta alipuusta.

Vasen alipuu:

Uusi juuri = { 2 } ≠ 5 tai 6, joten jatkamme rekursioamme

Uusi juuri = { 4 } , sen vasen ja oikea alipuu on tyhjä, palaamme tälle kutsulle NULL:n

Uusi juuri = { 5 }, arvo vastaa 5:tä, joten palauttaa solmun arvolla 5

Funktiokutsu juurille, jonka arvo on 2, palauttaa arvon 5

Oikea alipuu:

Root = { 3 } ≠ 5 tai 6, joten jatkamme rekursioamme

Juuri = { 6 } = 5 tai 6, palautamme tämän solmun arvolla 6

Juuri = { 7 } ≠ 5 tai 6, palautamme arvon NULL

Joten funktiokutsu juurille, jonka arvo on 3, palauttaa solmun arvolla 6

Koska sekä arvon 1 solmun vasen alipuu että oikea alipuu eivät ole NULL, joten 1 on LCA

Ratkaise ongelma noudattamalla alla olevia ohjeita:

Välitämme juuren apufunktiolle ja tarkistamme, vastaako juuren arvo jotakin n1:stä ja n2:sta.
- Jos KYLLÄ, palauta juuri
- muuten rekursiivinen kutsu vasemmalla ja oikealla alipuulla
Periaatteessa teemme ennakkotilauksen läpikulkua, tarkistamme ensin, vastaako root->value n1 tai n2. Siirrä sitten vasemmalla ja oikealla alipuulla.
Jos jokin juuri palauttaa yhden NULL-arvon ja toisen EI-NULL-arvon, palautamme vastaavan EI-NULL-arvon kyseiselle solmulle.
Solmu, joka palauttaa molemmat NON-NULL-arvot sekä vasemmalle että oikealle alipuulle, on alin yhteinen esi-isämme.

Alla on edellä mainitun lähestymistavan toteutus.

C++

/* C++ Program to find LCA of n1 and n2 using one traversal> >* of Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->avain = avain;> >temp->vasen = temp->right = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> struct> Node* findLCA(>struct> Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->avain == n1>> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->vasen = newNode(2);> >root->oikea = newNode(3);> >root->vasen->vasen = uusiSolmu(4);> >root->vasen->oikea = newNode(5);> >root->oikea->vasen = uusiSolmu(6);> >root->oikea->oikea = newNode(7);> >cout <<>'LCA(4, 5) = '>

  cout << '
LCA(4, 6) = '   cout << '
LCA(3, 4) = '   cout << '
LCA(2, 4) = '   return 0; } // This code is contributed by Aditya Kumar (adityakumar129)>

C

// C Program to find LCA of n1 and n2 using one traversalof> // Binary Tree> #include> #include> // A Binary Tree Node> typedef> struct> Node {> >struct> Node *left, *right;> >int> key;> } Node;> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp = (Node*)>malloc>(>sizeof>(Node));> >temp->avain = avain;> >temp->vasen = temp->right = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> Node* findLCA(Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->avain == n1>> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->vasen = newNode(2);> >root->oikea = newNode(3);> >root->vasen->vasen = uusiSolmu(4);> >root->vasen->oikea = newNode(5);> >root->oikea->vasen = uusiSolmu(6);> >root->oikea->oikea = newNode(7);> >printf>(>'LCA(4, 5) = %d'>, findLCA(root, 4, 5)->avain);> >printf>(>

'
LCA(4, 6) = %d'>

, findLCA(root, 4, 6)->avain);> >printf>(>

'
LCA(3, 4) = %d'>

, findLCA(root, 3, 4)->avain);> >printf>(>

'
LCA(2, 4) = %d'>

, findLCA(root, 2, 4)->avain);> >return> 0;> }> // This code is contributed by Aditya Kumar (adityakumar129)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> /* Class containing left and right child of current> >node and key value*/> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> >> >// Base case> >if> (node ==>null>)> >return> null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by returning root (Note that> >// if a key is ancestor of other, then the ancestor> >// key becomes LCA> >if> (node.data == n1> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ tree.findLCA(>4>,>5>).data);> >System.out.println(>'LCA(4, 6) = '> >+ tree.findLCA(>4>,>6>).data);> >System.out.println(>'LCA(3, 4) = '> >+ tree.findLCA(>3>,>4>).data);> >System.out.println(>'LCA(2, 4) = '> >+ tree.findLCA(>2>,>4>).data);> >}> }>

Python 3

# Python program to find LCA of n1 and n2 using one> # traversal of Binary tree> # A binary tree node> class> Node:> ># Constructor to create a new tree node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function returns pointer to LCA of two given> # values n1 and n2> # This function assumes that n1 and n2 are present in> # Binary Tree> def> findLCA(root, n1, n2):> ># Base Case> >if> root>is> None>:> >return> None> ># If either n1 or n2 matches with root's key, report> ># the presence by returning root (Note that if a key is> ># ancestor of other, then the ancestor key becomes LCA> >if> root.key>=>=> n1>or> root.key>=>=> n2:> >return> root> ># Look for keys in left and right subtrees> >left_lca>=> findLCA(root.left, n1, n2)> >right_lca>=> findLCA(root.right, n1, n2)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> # Driver code> if> __name__>=>=> '__main__'>:> > ># Let us create a binary tree given in the above example> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>).key)> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>).key)> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>).key)> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>).key)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# implementation to find lowest common> // ancestor of n1 and n2 using one traversal> // of binary tree> using> System;> // Class containing left and right> // child of current node and key value> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA> >// of two given values n1 and n2. This> >// function assumes that n1 and n2 are> >// present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> > node.data == n2)> >return> node;> >// Look for keys in left and right subtrees> >Node left_lca = findLCA(node.left, n1, n2);> >Node right_lca = findLCA(node.right, n1, n2);> >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree> >// and other is present in other, So this> >// node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or> >// right subtree is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >> >// Driver code> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> >+ tree.findLCA(4, 5).data);> >Console.WriteLine(>'LCA(4, 6) = '> >+ tree.findLCA(4, 6).data);> >Console.WriteLine(>'LCA(3, 4) = '> >+ tree.findLCA(3, 4).data);> >Console.WriteLine(>'LCA(2, 4) = '> >+ tree.findLCA(2, 4).data);> >}> }> // This code is contributed by pratham76>

Javascript

> >// JavaScript implementation to find> >// lowest common ancestor of> >// n1 and n2 using one traversal of binary tree> > >class Node> >{> >constructor(item) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = item;> >}> >}> > >//Root of the Binary Tree> >let root;> > >function> findlCA(n1, n2)> >{> >return> findLCA(root, n1, n2);> >}> > >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >function> findLCA(node, n1, n2)> >> > >root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >document.write(>'LCA(4, 5) = '> +> >findlCA(4, 5).data +>''>);> >document.write(>'LCA(4, 6) = '> +> >findlCA(4, 6).data +>''>);> >document.write(>'LCA(3, 4) = '> +> >findlCA(3, 4).data +>''>);> >document.write(>'LCA(2, 4) = '> +> >findlCA(2, 4).data +>''>);> > >

Lähtö

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Aika monimutkaisuus : O(N), koska menetelmä tekee yksinkertaisen puun läpikäymisen alhaalta ylös -tavalla.
Aputila: O(H), jossa H on puun korkeus.

Huomautus: Yllä oleva menetelmä olettaa sen avaimet ovat läsnä binääripuussa . Jos yksi avain on läsnä ja toinen puuttuu, se palauttaa nykyisen avaimen LCA:na (ihannetapauksessa olisi pitänyt palauttaa NULL). Voimme laajentaa tätä menetelmää käsittelemään kaikkia tapauksia tarkistamalla ensin, ovatko n1 ja n2 puussa, ja sitten etsimällä n1:n ja n2:n LCA. Tarkistaaksesi, onko solmu binääripuussa vai ei, käytä sitten puuta sekä n1 että n2 solmulle erikseen.

C++

/* C++ program to find LCA of n1 and n2 using one traversal> >of Binary Tree. It handles all cases even when n1 or n2> >is not there in Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->avain = avain;> >temp->vasen = temp->right = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given> // valuesn1 and n2.> struct> Node* findLCAUtil(>struct> Node* root,>int> n1,>int> n2)> > // Returns true if key k is present in tree rooted with root> bool> find(Node* root,>int> k)> find(root->oikein, k))> >return> true>;> >// Else return false> >return> false>;> > // This function returns LCA of n1 and n2 only if both n1> // and n2 are present in tree, otherwise returns NULL;> Node* findLCA(Node* root,>int> n1,>int> n2)> {> >// Return LCA only if both n1 and n2 are present in tree> >if> (find(root, n1) and find(root, n2))> >return> findLCAUtil(root, n1, n2);> >// Else return NULL> >return> NULL;> }> // Driver program to test above functions> int> main()> {> >// Let us create a binary tree given in the above> >// example> >Node* root = newNode(1);> >root->vasen = newNode(2);> >root->oikea = newNode(3);> >root->vasen->vasen = uusiSolmu(4);> >root->vasen->oikea = newNode(5);> >root->oikea->vasen = uusiSolmu(6);> >root->oikea->oikea = newNode(7);> >Node* lca = findLCA(root, 4, 5);> >if> (lca != NULL)> >cout <<>'LCA(4, 5) = '>

  else  cout << 'Keys are not present ';  lca = findLCA(root, 4, 10);  if (lca != NULL)  cout << '
LCA(4, 10) = '   else  cout << '
Keys are not present ';  return 0; } // This code is contributed by Kshitij Dwivedi // (kshitijdwivedi28)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >static> boolean> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >Node findLCAUtil(Node node,>int> n1,>int> n2)> >{> >// Base case> >if> (node ==>null>)> >return> null>;> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>)> >return> temp;> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2)> >return> lca;> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >Node lca = tree.findLCA(>4>,>5>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 5) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >lca = tree.findLCA(>4>,>10>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 10) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >}> }>

Python 3

''' Program to find LCA of n1 and n2 using one traversal of> >Binary tree> It handles all cases even when n1 or n2 is not there in tree> '''> # A binary tree node> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function return pointer to LCA of two given values> # n1 and n2> # v1 is set as true by this function if n1 is found> # v2 is set as true by this function if n2 is found> def> findLCAUtil(root, n1, n2, v):> ># Base Case> >if> root>is> None>:> >return> None> ># IF either n1 or n2 matches ith root's key, report> ># the presence by setting v1 or v2 as true and return> ># root (Note that if a key is ancestor of other, then> ># the ancestor key becomes LCA)> >if> root.key>=>=> n1:> >v[>0>]>=> True> >return> root> >if> root.key>=>=> n2:> >v[>1>]>=> True> >return> root> ># Look for keys in left and right subtree> >left_lca>=> findLCAUtil(root.left, n1, n2, v)> >right_lca>=> findLCAUtil(root.right, n1, n2, v)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> def> find(root, k):> ># Base Case> >if> root>is> None>:> >return> False> ># If key is present at root, or if left subtree or right> ># subtree , return true> >if> (root.key>=>=> k>or> find(root.left, k)>or> >find(root.right, k)):> >return> True> ># Else return false> >return> False> # This function returns LCA of n1 and n2 on value if both> # n1 and n2 are present in tree, otherwise returns None> def> findLCA(root, n1, n2):> ># Initialize n1 and n2 as not visited> >v>=> [>False>,>False>]> ># Find lca of n1 and n2 using the technique discussed above> >lca>=> findLCAUtil(root, n1, n2, v)> ># Returns LCA only if both n1 and n2 are present in tree> >if> (v[>0>]>and> v[>1>]>or> v[>0>]>and> find(lca, n2)>or> v[>1>]>and> >find(lca, n1)):> >return> lca> ># Else return None> >return> None> # Driver program to test above function> root>=> Node(>1>)> root.left>=> Node(>2>)> root.right>=> Node(>3>)> root.left.left>=> Node(>4>)> root.left.right>=> Node(>5>)> root.right.left>=> Node(>6>)> root.right.right>=> Node(>7>)> lca>=> findLCA(root,>4>,>5>)> if> lca>is> not> None>:> >print>(>'LCA(4, 5) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> lca>=> findLCA(root,>4>,>10>)> if> lca>is> not> None>:> >print>(>'LCA(4,10) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

using> System;> // c# implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >public> Node root;> >public> static> bool> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >public> virtual> Node findLCAUtil(Node node,>int> n1,> >int> n2)> >{> >// Base case> >if> (node ==>null>) {> >return> null>;> >}> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>) {> >return> temp;> >}> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>) {> >return> node;> >}> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >public> virtual> Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2) {> >return> lca;> >}> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Node lca = tree.findLCA(4, 5);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 5) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >lca = tree.findLCA(4, 10);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 10) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >}> }> // This code is contributed by Shrikant13>

Javascript

> // JavaScript implementation to find lowest> // common ancestor of n1 and n2 using one> // traversal of binary tree. It also handles> // cases even when n1 and n2 are not there in Tree> // Class containing left and right child> // of current node and key> class Node> {> >constructor(item)> >{> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> class BinaryTree{> > // Root of the Binary Tree> constructor()> {> >this>.root =>null>;> >this>.v1 =>false>;> >this>.v2 =>false>;> }> // This function returns pointer to LCA> // of two given values n1 and n2.> // v1 is set as true by this function> // if n1 is found> // v2 is set as true by this function> // if n2 is found> findLCAUtil(node, n1, n2)> {> > >// Base case> >if> (node ==>null>)> >{> >return> null>;> >}> > >// Store result in temp, in case of> >// key match so that we can search> >// for other key also.> >var> temp =>null>;> > >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as> >// true and return root (Note that if a key> >// is ancestor of other, then the ancestor> >// key becomes LCA)> >if> (node.data == n1)> >{> >this>.v1 =>true>;> >temp = node;> >}> >if> (node.data == n2)> >{> >this>.v2 =>true>;> >temp = node;> >}> > >// Look for keys in left and right subtrees> >var> left_lca =>this>.findLCAUtil(node.left, n1, n2);> >var> right_lca =>this>.findLCAUtil(node.right, n1, n2);> > >if> (temp !=>null>)> >{> >return> temp;> >}> > >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree and> >// other is present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >{> >return> node;> >}> > >// Otherwise check if left subtree or> >// right subtree is LCA> >return> left_lca !=>null> ? left_lca : right_lca;> }> // Finds lca of n1 and n2 under the> // subtree rooted with 'node'> findLCA(n1, n2)> {> > >// Initialize n1 and n2 as not visited> >this>.v1 =>false>;> >this>.v2 =>false>;> > >// Find lca of n1 and n2 using the> >// technique discussed above> >var> lca =>this>.findLCAUtil(>this>.root, n1, n2);> > >// Return LCA only if both n1 and n2> >// are present in tree> >if> (>this>.v1 &&>this>.v2)> >{> >return> lca;> >}> > >// Else return NULL> >return> null>;> }> }> // Driver code> var> tree =>new> BinaryTree();> tree.root =>new> Node(1);> tree.root.left =>new> Node(2);> tree.root.right =>new> Node(3);> tree.root.left.left =>new> Node(4);> tree.root.left.right =>new> Node(5);> tree.root.right.left =>new> Node(6);> tree.root.right.right =>new> Node(7);> var> lca = tree.findLCA(4, 5);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 5) = '> +> >lca.data +>' '>);> }>else> {> >document.write(>'Keys are not present'> +>' '>);> }> lca = tree.findLCA(4, 10);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 10) = '> +> >lca.data +>' '>);> }> else> {> >document.write(>'Keys are not present'> +>' '>);> }> // This code is contributed by rdtank> >

Lähtö

LCA(4, 5) = 2 Keys are not present>

Aika monimutkaisuus : O(N), koska menetelmä tekee yksinkertaisen puun läpikäymisen alhaalta ylös -tavalla.
Aputila: O(H), missä h on puun korkeus.

Aputietorakenteen käyttäminen (hash-taulukko):

The basic idea behind the 'Using an auxiliary data structure' approach for finding the lowest common ancestor of two nodes in a binary tree is to use a hash table or a map to store the parent pointers of each node. Once we have the parent pointers, we can traverse up from the first node and add all its ancestors to a set or a list. Then we can traverse up from the second node and check if each ancestor is already in the set or the list. The first ancestor that is already in the set or the list is the lowest common ancestor.>

Ota yllä oleva lähestymistapa käyttöön noudattamalla ohjeita:

Luo hash-taulukko tai kartta tallentaaksesi kunkin solmun pääosoittimet binääripuuhun.
Kulje binaaripuun läpi ja täytä hash-taulukko tai kartta kunkin solmun pääosoittimilla.
Aloita ensimmäisestä solmusta, kulje puuta ylöspäin ja lisää jokainen esi-isä joukkoon tai luetteloon.
Aloita toisesta solmusta, kulje puuta ylös ja tarkista, onko jokainen esi-isä jo joukossa tai luettelossa. Ensimmäinen esi-isä, joka on jo joukossa tai luettelossa, on alin yhteinen esi-isä.
Jos yhteistä esi-isää ei löydy, palauta nolla tai mikä tahansa muu arvo, joka ilmaisee yhteisen esivanhemman puuttumisen.

Alla on yllä olevan lähestymistavan toteutus:

C++

// C++ code to implement above approach> #include> #include> #include> #include> using> namespace> std;> // Definition of a binary tree node> struct> Node {> >int> data;> >Node* left;> >Node* right;> };> // Function to create a new binary tree node> Node* newNode(>int> data)> {> >Node* node =>new> Node;> >node->data = data;> >node->vasen = NULL;> >node->oikea = NULL;> >return> (node);> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> unordered_map buildParentMap(Node* root)> {> >unordered_map parentMap;> >parentMap[root] = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->vasemmalle) {> >parentMap[node->vasen] = solmu;> >queue.push_back(node->vasemmalle);> >}> >if> (node->oikealla) {> >parentMap[node->oikea] = solmu;> >queue.push_back(node->oikealla);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two nodes> // using an auxiliary data structure> int> findLCA(Node* root,>int> n1,>int> n2)> {> >// Build a hash table or a map of parent pointers for> >// each node in the tree> >unordered_map parentMap> >= buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node* p = NULL;> >Node* q = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->data == n1) {> >p = node;> >}> >if> (node->data == n2) {> >q = node;> >}> >if> (node->vasemmalle) {> >queue.push_back(node->vasemmalle);> >}> >if> (node->oikealla) {> >queue.push_back(node->oikealla);> >}> >}> >// Add all the ancestors of the first node to a set or a> >// list> >set ancestors;> >while> (p) {> >ancestors.insert(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if each> >// ancestor is already in the set or the list> >while> (q) {> >if> (ancestors.find(q) != ancestors.end()) {> >return> q> >->tiedot;>>>// already in the set or the list is> >// the lowest common ancestor> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> }> // Driver code> int> main()> {> >Node* root = newNode(1);> >root->vasen = newNode(2);> >root->oikea = newNode(3);> >root->vasen->vasen = uusiSolmu(4);> >root->vasen->oikea = newNode(5);> >root->oikea->vasen = uusiSolmu(6);> >root->oikea->oikea = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5) << endl;> >cout <<>'LCA(4, 6) = '> << findLCA(root, 4, 6) << endl;> >cout <<>'LCA(3,4) = '> << findLCA(root, 3, 4) << endl;> >cout <<>'LCA(2, 4) = '> << findLCA(root, 2, 4) << endl;> >return> 0;> }> // This code is contributed by Veerendra_Singh_Rajpoot>

Java

import> java.util.*;> // Definition of a binary tree node> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> Main {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Map buildParentMap(Node root)> >{> >Map parentMap =>new> HashMap();> >parentMap.put(root,>null>);> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.left !=>null>) {> >parentMap.put(node.left, node);> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.put(node.right, node);> >queue.add(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> findLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Map parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.data == n1) {> >p = node;> >}> >if> (node.data == n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >queue.add(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >Set ancestors =>new> HashSet();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.contains(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> ->1>;>// No common ancestor found> >}> >public> static> void> main(String[] args)> >{> >Node root =>new> Node(>1>);> >root.left =>new> Node(>2>);> >root.right =>new> Node(>3>);> >root.left.left =>new> Node(>4>);> >root.left.right =>new> Node(>5>);> >root.right.left =>new> Node(>6>);> >root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ findLCA(root,>4>,>5>));> >System.out.println(>'LCA(4, 6) = '> >+ findLCA(root,>4>,>6>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>3>,>4>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>2>,>4>));> >}> }>

Python 3

from> collections>import> deque> # Definition of a binary tree node> class> Node:> >def> __init__(>self>, data):> >self>.data>=> data> >self>.left>=> None> >self>.right>=> None> # Function to build a hash table or a map of parent> # pointers for each node in the tree> def> buildParentMap(root):> >parentMap>=> {}> >parentMap[root]>=> None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.left:> >parentMap[node.left]>=> node> >queue.append(node.left)> >if> node.right:> >parentMap[node.right]>=> node> >queue.append(node.right)> >return> parentMap> # Function to find the lowest common ancestor of two nodes> # using an auxiliary data structure> def> findLCA(root, n1, n2):> ># Build a hash table or a map of parent pointers for> ># each node in the tree> >parentMap>=> buildParentMap(root)> ># Find the nodes with values n1 and n2> >p, q>=> None>,>None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.data>=>=> n1:> >p>=> node> >if> node.data>=>=> n2:> >q>=> node> >if> node.left:> >queue.append(node.left)> >if> node.right:> >queue.append(node.right)> ># Add all the ancestors of the first node to a set or a> ># list> >ancestors>=> set>()> >while> p:> >ancestors.add(p)> >p>=> parentMap[p]> ># Traverse up from the second node and check if each> ># ancestor is already in the set or the list> >while> q:> >if> q>in> ancestors:> >return> q.data> >q>=> parentMap[q]> >return> ->1> # No common ancestor found> # Driver code> if> __name__>=>=> '__main__'>:> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>))> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>))> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>))> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>))>

C#

using> System;> using> System.Collections.Generic;> // Definition of a binary tree node> class> Node> {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> MainClass> {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Dictionary BuildParentMap(Node root)> >{> >Dictionary parentMap =>new> Dictionary();> >parentMap.Add(root,>null>);> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.left !=>null>)> >{> >parentMap.Add(node.left, node);> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >parentMap.Add(node.right, node);> >queue.Enqueue(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> FindLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Dictionary parentMap = BuildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.data == n1)> >{> >p = node;> >}> >if> (node.data == n2)> >{> >q = node;> >}> >if> (node.left !=>null>)> >{> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >queue.Enqueue(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >HashSet ancestors =>new> HashSet();> >while> (p !=>null>)> >{> >ancestors.Add(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>)> >{> >if> (ancestors.Contains(q))> >{> >return> q.data;> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> >}> >public> static> void> Main()> >{> >Node root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> + FindLCA(root, 4, 5));> >Console.WriteLine(>'LCA(4, 6) = '> + FindLCA(root, 4, 6));> >Console.WriteLine(>'LCA(3, 4) = '> + FindLCA(root, 3, 4));> >Console.WriteLine(>'LCA(2, 4) = '> + FindLCA(root, 2, 4));> >}> }> // This code is contributed by akashish__>

Javascript

// javascript code addition> // Definition of a binary tree node> class Node {> >constructor(item) {> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> function> buildParentMap(root) {> >const parentMap =>new> Map();> >parentMap.set(root,>null>);> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.left !=>null>) {> >parentMap.set(node.left, node);> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.set(node.right, node);> >queue.push(node.right);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two> // nodes using an auxiliary data structure> function> findLCA(root, n1, n2) {> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >const parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >let p =>null>, q =>null>;> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.data === n1) {> >p = node;> >}> >if> (node.data === n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >queue.push(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >const ancestors =>new> Set();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.has(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> -1;>// No common ancestor found> }> // Test the function> const root =>new> Node(1);> root.left =>new> Node(2);> root.right =>new> Node(3);> root.left.left =>new> Node(4);> root.left.right =>new> Node(5);> root.right.left =>new> Node(6);> root.right.right =>new> Node(7);> console.log(>'LCA(4, 5) = '> + findLCA(root, 4, 5));> console.log(>'LCA(4, 6) = '> + findLCA(root, 4, 6));> console.log(>'LCA(3, 4) = '> + findLCA(root, 3, 4));> console.log(>'LCA(2, 4) = '> + findLCA(root, 2, 4));> // The code is contributed by Nidhi goel.>

Lähtö

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3,4) = 1 LCA(2, 4) = 2>

Aika monimutkaisuus: O(n),

kuinka päästä eroon aikasilmukasta java

Annetun koodin aikamonimutkaisuus on O(n), missä n on binääripuun solmujen lukumäärä.

Pääkartan rakentaminen puun jokaiselle solmulle vaatii käyntiä jokaisessa solmussa kerran, mikä kestää O(n) aikaa. Solmujen löytäminen arvoilla n1 ja n2 vaatii käyntiä jokaisessa solmussa kerran, mikä vie myös O(n) aikaa. Kulkeminen ylös toisesta solmusta ja sen tarkistaminen, onko kukin esi-isä jo joukossa tai listassa kestää O(h) aikaa, missä h on binääripuun korkeus.

Pahimmassa tapauksessa binääripuun korkeus on O(n), jos binääripuu on vinossa. Siksi annetun koodin kokonaisaikakompleksisuus on O(n) + O(n) + O(n) = O(n).

Tilan monimutkaisuus: O(n),

Annetun koodin tilamonimutkaisuus on O(n) pahimmassa tapauksessa. Tämä johtuu siitä, että puun kullekin solmulle rakennetun emokartan koko on O(n). Lisäksi esivanhempien joukko voi sisältää myös kaikki binääripuun solmut pahimmassa tapauksessa, mikä myös vie O(n) tilaa. Lopuksi jono, jota käytetään binääripuun läpikulkuun, vie O(n) tilaa. Siksi annetun koodin kokonaisavaruuden kompleksisuus on O(n) + O(n) + O(n) = O(n).

Olemme keskustelleet tehokkaasta ratkaisusta LCA:n löytämiseen binäärihakupuusta. Binaarihakupuussa BST-ominaisuuksia käyttämällä voimme löytää LCA:n O(h)-ajassa, missä h on puun korkeus. Tällainen toteutus ei ole mahdollista Binaaripuussa, koska avaimet Binaaripuun solmut eivät seuraa mitään järjestystä.

Saatat haluta nähdä myös alla olevat artikkelit:
LCA käyttäen Parent Pointer -osoitinta
Alin yhteinen esi-isä binäärihakupuussa.
Etsi LCA binaaripuusta RMQ:n avulla