Luhn-algoritmi, joka tunnetaan myös nimellä moduuli 10 tai kohti 10 Algoritmi on yksinkertainen tarkistussummakaava, jota käytetään useiden eri tunnistenumeroiden, kuten luottokorttien numeroiden, IMEI-numeroiden ja Kanadan sosiaalivakuutusnumeroiden, vahvistamiseen. LUHN-kaavan loi 1960-luvun lopulla ryhmä matemaatikoita. Pian tämän jälkeen luottokorttiyhtiöt ottivat sen käyttöön. Koska algoritmi on julkinen, sitä voivat käyttää kuka tahansa. Useimmat luottokortit ja monet valtion tunnusnumerot käyttävät algoritmia yksinkertaisena tapana erottaa kelvolliset numerot väärin kirjoitetuista tai muuten virheellisistä numeroista. Se on suunniteltu suojaamaan vahingossa tapahtuvilta virheiltä, ei haitallisilta hyökkäyksiltä.
Luhn-algoritmin vaiheet
Ymmärretään algoritmi esimerkin avulla:
Harkitse esimerkkiä tilinumerosta 79927398713 .
Vaihe 1 – Alkaen oikeanpuoleisesta numerosta, tuplaa jokaisen toisen numeron arvo,
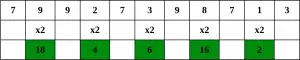
Vaihe 2 – Jos luvun kaksinkertaistamisesta saadaan kaksinumeroinen luku, eli suurempi kuin 9 (esim. 6 × 2 = 12), lisää tulon numerot (esim. 12: 1 + 2 = 3, 15: 1 + 5 = 6), saadaksesi yksinumeroisen luvun.

Vaihe 3 – Ota nyt kaikkien numeroiden summa.
mysql lisää

Vaihe 4 – Jos kokonaismoduuli 10 on yhtä suuri kuin 0 (jos summa päättyy nollaan), luku on voimassa Luhnin kaavan mukaan; muuten se ei ole voimassa.

Koska summa on 70, joka on 10:n kerrannainen, tilinumero on mahdollisesti kelvollinen.
Idea on yksinkertainen; kuljemme lopusta. Jokaisen toisen numeron kohdalla tuplataan se ennen sen lisäämistä. Lisäämme kaksinkertaisen luvun kaksi numeroa.
Toteutus:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
menetelmän alamerkkijono java
>
>
Python 3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
java-viittaustyypit
>
C#
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)>> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
Java-esimerkki
>
>
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
>Lähtö
This is a valid card>
Luhn-algoritmi havaitsee kaikki yksinumeroiset virheet sekä lähes kaikki vierekkäisten numeroiden transponoinnit.
