- Olemme tutkineet strategioita, jotka voivat järkeillä joko eteenpäin tai taaksepäin, mutta näiden kahden suunnan sekoitus sopii monimutkaisen ja suuren ongelman ratkaisemiseen. Tällainen sekastrategia mahdollistaa sen, että ensin ratkaistaan suurin osa ongelmasta ja sitten palataan takaisin ja ratkaistaan pienet ongelmat, jotka syntyvät yhdistämällä ongelman suuria osia. Tällaista tekniikkaa kutsutaan Keino-päämäärä-analyysi .
- Means-Ends Analysis on ongelmanratkaisutekniikoita, joita käytetään tekoälyssä rajoittamaan hakua tekoälyohjelmissa.
- Se on sekoitus taaksepäin- ja eteenpäinhakutekniikkaa.
- MEA-tekniikan esittelivät ensimmäisen kerran vuonna 1961 Allen Newell ja Herbert A. Simon ongelmanratkaisutietokoneohjelmassaan, joka sai nimen General Problem Solver (GPS).
- MEA-analyysiprosessi keskittyi nykytilan ja tavoitetilan välisen eron arviointiin.
Miten keinojen ja päämäärien analyysi toimii:
Keinopäämäärien analyysiprosessia voidaan soveltaa rekursiivisesti ongelmaan. Se on strategia, jolla ohjataan hakua ongelmanratkaisussa. Seuraavat ovat tärkeimmät vaiheet, jotka kuvaavat MEA-tekniikan toimintaa ongelman ratkaisemiseksi.
- Arvioi ensin alkutilan ja lopullisen tilan välinen ero.
- Valitse eri operaattorit, joita voidaan käyttää jokaiselle erolle.
- Käytä operaattoria jokaisessa erossa, mikä pienentää eroa nykyisen tilan ja tavoitetilan välillä.
Operaattorin alitavoitteet
MEA-prosessissa havaitsemme erot nykytilan ja tavoitetilan välillä. Kun nämä erot ilmenevät, voimme käyttää operaattoria erojen vähentämiseksi. Mutta joskus on mahdollista, että operaattoria ei voida soveltaa nykyiseen tilaan. Joten luodaan nykyisen tilan aliongelma, jossa operaattoria voidaan käyttää, sellainen taaksepäin ketjutus, jossa valitaan operaattorit ja sitten asetetaan alitavoitteet operaattorin edellytysten määrittämiseksi. Operaattorin alitavoitteet .
Algoritmi keinojen ja päämäärien analyysille:
Otetaan nykyinen tila NYKYISEEN ja Tavoitetila TAVOITTEENA, sitten seuraavat MEA-algoritmin vaiheet.
- Valitse uusi operaattori O, joka soveltuu nykyiselle erolle, ja jos sellaista ei ole, signaalivirhe.
- Yritä käyttää operaattoria O arvoon CURRENT. Tee kuvaus kahdesta tilasta.
i) O-Start, tila, jossa O:n ennakkoehdot täyttyvät.
ii) O-tulos, tila, joka syntyisi, jos O käytettäisiin O-alkussa. - Jos
(Ensimmäinen osa<------ mea (current, o-start)< strong>
Ja
(Viimeinen osa<----- mea (o-result, goal)< strong>, onnistuvat, anna sitten signaali Onnistuminen ja palauttaa tuloksen, kun yhdistetään FIRST-PART, O ja LAST-PART.
Yllä käsitelty algoritmi soveltuu paremmin yksinkertaiseen ongelmaan, eikä se sovellu monimutkaisten ongelmien ratkaisemiseen.
Esimerkki keskimääräisestä analyysistä:
Otetaan esimerkki, jossa tiedämme alkutilan ja tavoitetilan alla esitetyllä tavalla. Tässä tehtävässä meidän on saatava tavoitetila etsimällä erot lähtötilan ja tavoitetilan välillä ja käyttämällä operaattoreita.
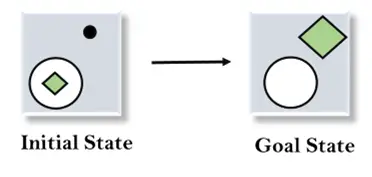
Ratkaisu:
Yllä olevan ongelman ratkaisemiseksi etsimme ensin alkutilojen ja tavoitetilojen väliset erot ja jokaiselle erolle generoimme uuden tilan ja käytämme operaattoreita. Operaattoreita, joita meillä on tähän ongelmaan, ovat:
globaali var in js
1. Alkutilan arvioiminen: Ensimmäisessä vaiheessa arvioimme alkutilan ja vertaamme alkutilaa ja tavoitetilaa löytääksemme erot molempien tilojen välillä.

2. Poista-operaattorin käyttäminen: Kuten voimme tarkistaa, ensimmäinen ero on, että maalitilassa ei ole pistesymbolia, joka on läsnä alkutilassa, joten käytämme ensin Poista operaattori poistaaksesi tämän pisteen.

3. Move Operatorin käyttäminen: Delete-operaattorin käyttöönoton jälkeen tapahtuu uusi tila, jota verrataan jälleen tavoitetilaan. Näiden tilojen vertailun jälkeen on toinen ero, että neliö on ympyrän ulkopuolella, joten käytämme Siirrä operaattoria .

4. Expand Operatorin käyttäminen: Nyt kolmannessa vaiheessa luodaan uusi tila, jota verrataan tavoitetilaan. Tilojen vertailun jälkeen on vielä yksi ero, joka on neliön koko, joten käytämme sitä Laajenna operaattoria , ja lopuksi se luo tavoitetilan.

