Prosenttiosuus – Matematiikassa prosenttiluku on luku tai suhde, joka merkitsee murto-osaa sadasta. Se on menetelmä, jolla ilmaistaan kahden luvun välinen dimensioton suhde, joka on samanlainen kuin suhdeluvut, murtoluvut ja desimaalit. Prosenttiosuudet ilmaistaan yleensä symbolilla % numeron perässä. sana Prosenttiosuus syntyi latinan sanasta per sata joka tarkoittaa sadalla . Se on kahden luvun välinen dimensioton suhde. Sitä merkitään usein merkillä % tai prosenttia tai pct .
Tässä artikkelissa käsittelemme prosenttiosuus, mukaan lukien sen määritelmä, esimerkit, prosenttikaava, kuinka prosentti lasketaan jne.
Esimerkkejä prosenteista ovat:
- 10% on 10/100, eli 1/10 luvusta
- 20% on 20/100, eli 1/5 numerosta
Tässä artikkelissa opitaan yksityiskohtaisesti prosenttiosuuksista, prosenttikaavoista, prosenttiosuuksien laskemisesta ja muista.
Sisällysluettelo
- Mikä on prosenttiosuus?
- Esimerkkejä prosenteista
- Prosenttikaava
- Kuinka laskea prosenttiosuus numerosta?
- Prosenttierokaava
- Prosenttikorotuksen kaava
- Prosenttivähennyskaava
- Kuinka laskea prosenttiosuus?
- Prosentin muuntaminen murto-osiksi
- Murto-osan muuntaminen prosenteiksi
- Prosenttikaavio
- Prosenttitaulukko
- Ero prosentin ja prosentin välillä
- Prosentti matematiikassa
- Prosenttitemppuja
- Kuinka laskea pisteiden prosenttiosuus
- Prosenttilaskin
- Ratkaistu esimerkki prosenttiosuudesta
- Harjoittele prosenttikysymyksiä
Mikä on prosenttiosuus?
A f suhdetta, jonka nimittäjä on 100, kutsutaan prosentiksi eli kaikista murtoluvuista, joissa nimittäjä on 100, voimme poistaa nimittäjän ja laittaa %-merkin.
Esimerkiksi, murto-osa 23/100 voidaan kirjoittaa 23 %:ksi . Tämä on myös päinvastoin, eli mikä tahansa prosenttimerkki voidaan helposti korvata muuttamalla luku murto-osaksi nimittäjällä 100. Esimerkiksi 45 % voidaan muuntaa murto-osuudeksi 45/100.
- Prosentteja kutsutaan myös ulottumattomia lukuja , koska niillä ei ole ulottuvuutta. Ne ovat kahden samankokoisen luvun suhde. Jos sanomme 10 prosenttia luvusta, se tarkoittaa 10 prosenttia sen kokonaisuudesta.
- Prosentit voivat myös olla esitetään desimaaleina Arvot, kuten 0,5%, 0,75% jne.
Tarkistaa: Prosentit – soveltuvuuskysymykset ja vastaukset
Esimerkkejä prosenteista
Joitakin esimerkkejä fraktioista ovat mm ,
- Jos Kabir saa matematiikan kokeessa 95 pistettä 100:sta, se muutetaan murto-osaksi 95/100 = 95 %
- Jos ehdokas A saa 2450 ääntä 10 000 äänestä, se esitetään prosentteina 2450/1000 = 24,5/100 = 24,5 %
Samalla lailla,
- 10/100 prosentteina = 10 %
- 50/100 prosentteina = 50 %
- 100/100 prosentteina = 100 %
Alla olevassa kuvassa on esimerkkejä, joissa prosenttiosuutta käytetään.

Prosenttikaava
Prosenttiosuuskaava on kaava, jota käytetään määrittämään määrän tai osuuden sadassa. Joten prosenttiosuuden laskemiseen tarvitsemme periaatteessa kolme muuttujaa. Ensin kokonaisarvo V 1 , nykyarvo V 2 , ja prosenttiarvo P. Tämän algebrallinen yhtälö on:
Prosenttiosuus (P%) = (osia (V 2 ) / Kokonainen (V 1 )) × 100

Kuinka laskea prosenttiosuus numerosta?
Prosenttiosuuden laskeminen on hyvin yksinkertaista, sinun tarvitsee vain käyttää alla mainittua kaavaa:
Prosenttiluku = Prosentti/100 × Luku
Esimerkki:
Laske 5 % 50:stä
5 % 50:stä = 5/100 × 50
5 % 50:stä = 0,05 × 50
5 % 50:stä = 2,50
Prosenttierokaava
Prosenttiero tai prosentuaalinen muutos kaava lasketaan, kun kahden arvon erotus jaetaan samojen arvojen keskiarvolla. Voidaan sanoa, että prosenttieron avulla lasketaan arvon muutos tietyllä ajanjaksolla. Matemaattisesti meidät voidaan kirjoittaa muodossa
Tarkistaa: Prosentin peruskäsite
Prosenttiero = (absoluuttinen ero / keskiarvo) × 100
Esimerkki: Prosenttiero 50:n ja 100:n välillä on:
= |50-100|/ {(50+100)/2} × 100
= 50/75 × 100
= 66,66 %
Se ilmaistaan suhdelukuna ja on yksikkötön luku
Prosenttikorotuksen kaava
Voimme käyttää prosenttierokaavaa löytääksemme arvon muutoksen, kun se kasvaa ajan kuluessa. The prosentin lisäyskaava on annettu alla,
Prosenttikorotus = (Lisää arvoa – alkuperäinen arvo / keskiarvo) × 100
Prosenttivähennyskaava
Voimme käyttää prosenttierokaavaa löytääksemme arvon muutoksen, kun se pienenee tietyn ajanjakson aikana. The prosentin vähennyskaava on annettu alla,
Vähennysprosentti = (Alkuperäinen arvo – Pienennä arvoa / Keskiarvo) × 100
Huomautus:
- Jos saatu arvo on negatiivinen prosenttilisäyskaavaa laskettaessa, se on itse asiassa prosentuaalinen lasku.
- Jos saatu arvo on negatiivinen laskettaessa prosenttilaskukaavaa, se on itse asiassa prosentuaalinen lisäys.
- Prosenttimuutosta käytetään myös etsimään prosenttivirheitä matematiikassa, fysiikassa ja kemiassa.
Kuinka laskea prosenttiosuus?
Tärkein kysymys on, kuinka prosentti lasketaan. Prosentit voidaan siis helposti laskea, kun arvot annetaan murto-osina, joiden nimittäjä on 100. Jos ei, meidän on muutettava annettu murto-osa murto-osaksi, jonka nimittäjä on 100, ja sitten prosenttiluku on helppo laskea.
Tarkistaa: Kuinka laskea prosenttiosuus?
Jos esimerkiksi 65/100 on laskettava prosentteina, niin vastaus voidaan helposti laskea poistamalla nimittäjä 100 ja käyttämällä %-symbolia eli 65%.
merkkijonon java arvo
Esimerkki: Muunna 0,76 prosentiksi.
Ratkaisu:
0,76 = 0,76/1
0,76 = 76/100
0,76 = 76 %
Kuinka laskea prosenttiosuus, kun summa on 100?
Jos jossakin skenaariossa kokonaisarvo on 100, prosenttiosuuden laskeminen on erittäin helppoa, koska itse numero (arvon osoittajassa) edustaa prosenttiosuutta ja %-symboli lisätään.
Esimerkki: Oletetaan, että luokan edustajan valinnassa oppilas A sai 69 ääntä ja opiskelija B 31 ääntä, niin lasketaan A:n prosenttiosuus äänistä.
Ratkaisu:
Ääniä yhteensä = 69 + 31 = 100
A sai ääntä = 69
A:n äänet (prosentteina) = 69/100 = 69 %
Kuinka laskea prosenttiosuus, kun summa EI ole 100?
Jos kokonaisarvo missään skenaariossa ei ole 100, lasketaan prosenttiosuus tekemällä murto-osaan kokonaisarvo 100 ja osoittajaarvoista tulee prosenttiosuus.
Esimerkki: Oletetaan, että Kabirilla on 6 sinistä palloa, 8 punaista palloa ja 6 keltaista palloa, kuinka monta punaista palloa hänellä on?
Ratkaisu:
Pallot yhteensä = punaiset pallot + siniset pallot + keltaiset pallot
= 8 + 6 + 6 = 20 palloa
Punaiset pallot = 8 palloa
Punaisten pallojen prosenttiosuus = 8/20
= (8/20) × (5/5) = 40/100 = 40 %
Prosentin muuntaminen murto-osiksi
Joissakin tapauksissa meille tarjotaan prosenttiosuus, ja se on muutettava a murto-osa määrä. Prosenttiosuuksien muuntaminen murtoluvuiksi edellyttää joitakin laskelmia. Voimme käyttää kaavaa,
Tarkistaa: Ongelmia prosenteissa
Murtoluku = Prosentti/100
Saatuaan sen vähentää sitä edelleen. Esimerkiksi,
- 25 %:n osa = 25/100 = 1/4
- 50 %:n osa = 50/100 = 1/2
- 75 %:n osuus = 75/100 = 3/4
- 90 %:n osa = 90/100 = 9/10
Murto-osan muuntaminen prosenteiksi
Murtoluvun muuntamiseksi prosentteiksi oletetaan, että murto-osa edustaa a/b:tä, jossa a on osa kokonaisuutta b. Kerrotaan osoittaja ja nimittäjä 100:lla.
Tiedämme, että 1/100 = 1 %
Siksi, yhtälö voidaan kirjoittaa seuraavasti,
a/b × 100 %.
Siten, muuntaaksesi murto-osan prosentiksi, kerro murto-osa 100:lla.
Prosenttikaavio
Katsotaan prosenttikaavio murtoluvuista, jotka on muunnettu prosenteiksi,
Prosenttikaavio | |||
|---|---|---|---|
| Murto-osa | Prosenttiosuus | Murto-osa | Prosenttiosuus |
1/1 | 100 % | 1/11 | 9,09 % |
1/2 | viisikymmentä% | 1/12 | 8,33 % |
1/3 | 33,33 % | 1/13 | 7,69 % |
1/4 | 25 % | 1/14 | 7,14 % |
1/5 | kaksikymmentä% | 1/15 | 6,66 % |
1/6 | 16,66 % | 1/16 | 6,25 % |
1/7 | 14,28 % | 1/17 | 5,88 % |
1/8 | 12,5 % 10/50 | 1/18 | 5,55 % |
1/9 | 11,11 % | 1/19 | 5,26 % |
1/10 | 10 % | 1/20 | 5 % |
Prosenttitaulukko
Alla lisätty kuva näyttää prosenttitaulukon,
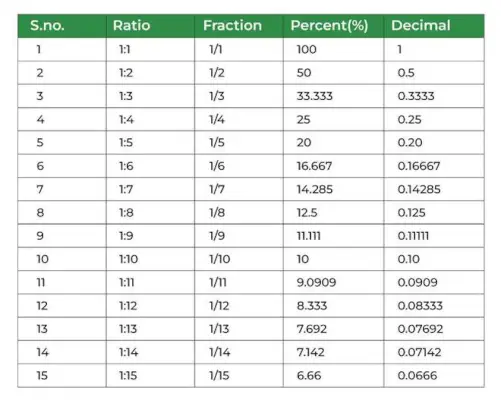
Ero prosentin ja prosentin välillä
Sanat prosenttiosuus ja prosentti liittyvät toisiinsa, mutta molemmilla on ero. Prosentin mukana on aina numero, esimerkiksi 25 %.
Prosenttiosuus ei tarvitse numeroa termin mukana.
Esimerkiksi vuonna 2022 äänestykseen osallistuneiden prosenttiosuus on suurempi kuin vuonna 2021 osallistuneiden prosenttiosuus.
Murtoluvut, desimaalit, suhteet ja prosentit liittyvät myös toisiinsa.
Prosentti matematiikassa
Matematiikassa prosenttiosuus kirjoitetaan kolmella mahdollisella tuntemattomalla ja muuttujalla. Kolme termiä tunnetaan:
- Prosenttiosuus
- Osa
- Pohja
Esimerkiksi 50 % 400:sta on 200. Tässä 50 on prosenttiosuus, 400 on perusta ja 200 on osa.
Esimerkki: Jos 25 % 200:sta on 50, selitä laskennan eri termit.
25 % 400:sta on 50. Tässä 25 on prosenttiosuus, 200 on perusta ja 50 on osa.
Murtolukuna se voidaan kirjoittaa seuraavasti,
Osa/pohja = 25/200 = 1/4
1/4 on saatu murto-osa. Olemme kuitenkin oppineet muuttamaan murtoluvut prosenteiksi. Siksi kerro 1/4 100:lla,
1/4 × 100 = 25 %.
Prosenttitemppuja
On olemassa prosenttitemppuja, joita voidaan käyttää laskettaessa lukujen prosenttiosuutta. Alla annettu temppu on eniten käytetty,
% x y:stä = % y x:stä
Esimerkki: Ratkaise 300 % 50:stä.
Tässä 300 % 50:stä ratkaiseminen voi olla hieman pitkää ja hankalaa. Temppua käyttämällä se voidaan kuitenkin ratkaista helposti,
%x y:stä = %y x:stä
300 % 50:stä = 50 % 300:sta
Nyt 50 %:n ratkaiseminen 300:sta on suhteellisen helppoa. 50 % 300:sta on vain puolet 300:sta. Siksi 50 % 300:sta on 150.
Siksi 300 % 50:stä on 150.
Kuinka laskea pisteiden prosenttiosuus
Prosenttia käytetään enimmäkseen opiskelijoille laskettaessa pisteitä. Opiskelijoiden arvosanat ovat suhteessa kokonaispisteisiin. Tämä murto-osa muunnetaan prosenteiksi kertomalla se 100:lla. Tällä tavalla voimme laskea pisteet prosentteina. Katsotaanpa joitain esimerkkejä prosentteina saaduista pisteistä,
| Pisteitä saatu | Pisteitä yhteensä | Pisteet prosentteina (%) |
|---|---|---|
| viisikymmentä | 100 | 50/100 × 100 = 50 % |
| 25 | viisikymmentä | 25/50 × 100 = 50 % |
| 80 | 100 | 80/100 × 100 = 80 % |
| 33 | 100 | 33/100 × 100 = 33 % |
Prosenttilaskin
Prosenttilaskin on ilmainen työkalu, joka on valmistettu osoitteessa techcodeview.com jota käytetään prosenttiosuuden löytämiseen, jos on annettu kaksi tai useampia lukuja. Tarkista alla oleva prosenttilaskuri:
Tarkistaa: Prosenttilaskin
Lue lisää,
- Murtoluvut
- Suhde ja suhteet kaava
- Prosenttituottokaava
Ratkaistu esimerkki prosenttiosuudesta
Joitakin esimerkkejä prosenteista ovat mm.
Esimerkki 1: Etsi 15 % 500:sta.
Ratkaisu:
Voimme löytää prosenttiosuuden kaavalla,
SISÄÄN2= P × V1
SISÄÄN2= 15 % × 500
SISÄÄN2= (15 × 500) / 100
SISÄÄN2= 75.
Siten 15 % 500:sta on 75.
Tarkistaa: Prosenttikysymykset
Esimerkki 2: Etsi 4 % 1300:sta.
Ratkaisu:
Voimme löytää prosenttiosuuden kaavalla,
SISÄÄN2= P × V1
SISÄÄN2= 4 % × 1300
SISÄÄN2= (4 × 1300) / 100
SISÄÄN2= 52.
Näin ollen 4 % 1300:sta on 52.
kuinka lähettää merkkijono int: hen javassa
Esimerkki 3: Mikä prosenttiosuus on 1 3000:sta?
Ratkaisu:
Voimme löytää prosenttiosuuden kaavalla,
SISÄÄN2= P × V1
P = V2/ SISÄÄN1
P = 1/3000
Siten P% = 1/3000 × 100
P % = (1/30) %
Siten (1/30) % vuodesta 2000 on 500.
Esimerkki 4: Jos 10 % x:stä on 900. Etsi x.
Ratkaisu:
Löydämme prosenttiosuuden kaavasta,
SISÄÄN2= P × V1
SISÄÄN1= V2/P
SISÄÄN1= (V2× 100 ) / P %
SISÄÄN1= (900 × 100) / 10
SISÄÄN1= 9000
Siten x:n arvo on 9000.
Esimerkki 5: Etsi vihreiden lohkojen prosenttiosuuden arvo kussakin tapauksessa.
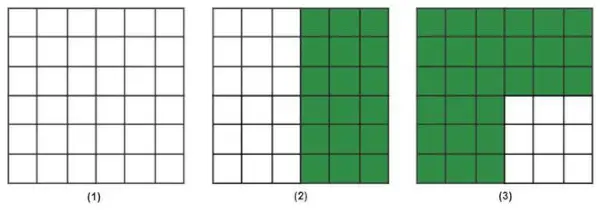
Ratkaisu:
Ensimmäisessä tapauksessa vihreät lohkot ovat 0 ja lohkojen kokonaismäärä on 36.
Siksi,
Vihreiden lohkojen prosenttiosuus = 0/36 × 100 = 0%.
Toisessa tapauksessa vihreitä lohkoja on 18 ja lohkojen kokonaismäärä on 36.
Siksi,
Vihreiden lohkojen prosenttiosuus = 18/36 × 100 = 50 %.
Kolmannessa tapauksessa vihreitä lohkoja on 27 ja tiiliä yhteensä 36.
Siksi,
Vihreiden lohkojen prosenttiosuus = 27/36 × 100 = 75 %.
Esimerkki 6: Mikä prosenttiosuus on 15/50?
Alkuperäinen arvo = 15
Kokonaisarvo = 50
Prosenttikaava on,
Prosenttiosuus = (alkuperäinen arvo/kokonaisarvo) × 100
= 15/50 × 100
= 30 %
Esimerkki 7: Kuinka monta prosenttia 80:stä on 20?
Alkuperäinen arvo = 20
Kokonaisarvo = 80
Prosenttikaava on,
Prosenttiosuus = (alkuperäinen arvo/kokonaisarvo) × 100
= 20/80 × 100
= 25 %
Harjoittele prosenttikysymyksiä
Q1: Poika sai yhteensä 450 markkaa 500:sta. Etsi prosenttiosuus pisteistä.
Q2: Selvitä puhtaiden kultahiukkasten prosenttiosuus 18 karaatissa kultaa, koska 24 karaatin kulta on puhdasta kultaa.
Q3: 5 litran happopullon pitoisuus on 10 %. Etsi liuoksen puhtaan hapon pitoisuus.
Q4: Ram sai 223 pistettä 600:sta ja epäonnistui kokeessa 17 pisteellä. Etsi pisteen ohitusprosentti.
Johtopäätös – prosenttiosuus
Prosentit ovat kuin universaali kieli mittasuhteille. Murtolukujen tai desimaalien kanssa painimisen sijaan voimme käyttää prosenttiosuudet ilmaisemaan mitä tahansa kokonaisuuden osaa 100:sta . Tämä tekee asioiden vertaamisesta helppoa, onko se ymmärrystä alennusmyynnistä , visualisoimalla kyselyn tuloksia tai noudattamalla reseptiä. Jokapäiväisistä tehtävistä monimutkaisiin tietojen analysointiin, prosenttiosuudet ovat tehokas työkalu maailmamme ymmärtämiseen osa kerrallaan.
Prosenttia koskevat usein kysytyt kysymykset
Mikä on 100 %:n prosenttiosuus?
Prosentti 100 % on itse asiassa 100
Miten määrittelet prosentin?
Prosenttiosuus on tapa ilmaista osa jostakin kokonaisuuteen verrattuna, kirjoitettuna sadan murto-osana.
Kuinka monta prosenttia 1 vuodesta on 1 päivä?
Laskeaksemme 1 vuoden prosenttiosuuden, jota 1 päivä edustaa, voimme jakaa yhden päivän päivien määrän yhden vuoden päivien lukumäärällä ja kertoa sitten 100 %:lla (ilmaistaksesi sen prosentteina).
Mikä on CGPA-prosentti?
CGPA-muunnos prosentiksi on yhtä helppoa kuin CGPA:n kertominen 9,5:llä.
Mikä on prosenttiosuus?
Prosenttiluku on lukujen esitys, jonka sanan kirjaimellinen merkitys prosenttiosuus on 100:sta. Prosenttiosuuksissa arvo esitetään 100:sta.
Mikä on prosenttiosuuden symboli?
Prosentin symboli on %. Se tunnetaan myös prosentteina.
Kuinka laskea prosenttiosuus?
Voit laskea luvun prosenttiosuuden jakamalla saatu luku kokonaisluvuilla ja kertomalla murto-osan 100:lla
Mikä on prosenttimuutos?
Luvun prosenttimuutos on prosenttimuutos vanhasta arvosta uuteen arvoon. Se lasketaan kaavalla,
Muutosprosentti = {(Vanhan ja uuden arvon välinen ero) / Vanha arvo} × 100.
Mitä ovat esimerkkejä prosenteista?
Prosenttia käytetään hyvin usein jokapäiväisessä elämässämme, tässä on joitain esimerkkejä prosenttiosuuden käytöstä tosielämässä.
- Erityyppisten ravintoaineiden prosenttiosuudet näkyvät ruokapakkausten takana.
- Akku näyttää tehonsa prosentteina puhelimissamme.
- Opiskelijoiden tenttipisteiden prosenttiosuus.
Voiko prosenttiluku ylittää 100?
Kyllä, prosentin arvo voi olla suurempi kuin 100, jos annettu arvo on suurempi kuin alkuperäinen arvo. Esimerkiksi 40/20 on 200 %.
