Rekursiivinen funktio voidaan määritellä rutiiniksi, joka kutsuu itseään suoraan tai epäsuorasti.

Toisin sanoen rekursiivinen funktio on funktio, joka ratkaisee ongelman ratkaisemalla saman ongelman pienempiä esiintymiä. Tätä tekniikkaa käytetään yleisesti ohjelmoinnissa ratkaisemaan ongelmia, jotka voidaan jakaa yksinkertaisempiin, samankaltaisiin osaongelmiin.

matematiikka pow java

Rekursiivisen funktion tarve:

Rekursiivinen funktio on funktio, joka ratkaisee ongelman ratkaisemalla saman ongelman pienempiä esiintymiä. Tätä tekniikkaa käytetään usein ohjelmoinnissa ratkaisemaan ongelmia, jotka voidaan jakaa yksinkertaisempiin, samankaltaisiin osaongelmiin.

1. Monimutkaisten tehtävien ratkaiseminen:

Rekursiiviset funktiot jakavat monimutkaiset ongelmat saman ongelman pienempiin esiintymiin, jolloin tuloksena on kompakti ja luettava koodi.

2. Haja ja hallitse:

Rekursiiviset funktiot soveltuvat jakaa ja hallitse -algoritmeihin, kuten yhdistämis- ja pikalajitteluun, ongelmien jakamiseen pienempiin osaongelmiin, niiden ratkaisemiseen rekursiivisesti ja ratkaisujen yhdistämiseen alkuperäisen ongelman kanssa.

tärkeä

3. Perääntyminen :

Rekursiivinen backtracking on ihanteellinen ongelmien, kuten N-Queens ja Sudoku, tutkimiseen ja ratkaisemiseen.

4. Dynaaminen ohjelmointi:

Rekursiiviset funktiot ratkaisevat tehokkaasti dynaamisia ohjelmointiongelmia ratkaisemalla aliongelmia ja yhdistämällä niiden ratkaisut kokonaiseksi ratkaisuksi.

5. Puu ja kaaviorakenteet:

Rekursiiviset funktiot ovat erinomaisia ​​puu- ja graafirakenteiden käsittelyssä, mikä yksinkertaistaa läpikulku- ja kuviontunnistustehtäviä .

Kuinka kirjoittaa rekursiivinen funktio:

Rekursiivisen funktion osat:

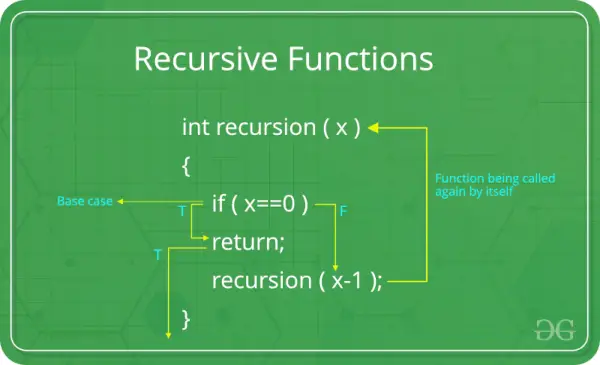
Perustapaus: Jokaisella rekursiivisella funktiolla on oltava peruskirjain. Perustapaus on yksinkertaisin skenaario, joka ei vaadi lisärekursiota. Tämä on lopetusehto, joka estää funktiota kutsumasta itseään loputtomiin. Ilman asianmukaista perustapausta rekursiivinen funktio voi johtaa äärettömään rekursioon.

Rekursiivinen tapaus: Rekursiivisessa tapauksessa funktio kutsuu itseään muokatuilla argumenteilla. Tämä on rekursion ydin – suuremman ongelman ratkaiseminen jakamalla se saman ongelman pienempiin esiintymiin. Rekursiivisen tapauksen tulisi siirtyä lähemmäksi perustapausta jokaisen iteroinnin yhteydessä.

takaisinsoitto helvetti javascriptissä

Tarkastellaanpa esimerkkiä luvun tekijä :

Tässä esimerkissä perustapaus on kun n On 0 , ja funktio palauttaa 1 . Rekursiivinen tapaus moninkertaistuu n parametrilla kutsutun funktion tuloksella n-1 . Prosessi jatkuu, kunnes perustapaus saavutetaan.

suunnittelukuvioita java

On oleellista varmistaa, että rekursiivisella funktiolla on oikea perustapaus ja että rekursiiviset kutsut johtavat perustapaukseen, muuten proseduuri saattaa jatkua toistaiseksi, mikä johtaa pinon ylivuotoon (joka ylittää funktiokutsuille varatun käytettävissä olevan muistin).

Alla on luvun faktoriaalin toteutus:

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout << 'Factorial of ' << n  << ' is:' << factorial(n);  return 0; }>

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } }>

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))>

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } }>

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();>

Factorial of 4 is:24>

Aika monimutkaisuus: Päällä)
Aputila: Päällä)