Relaatioalgebra on proseduurillinen kyselykieli. Se antaa vaiheittaisen prosessin kyselyn tuloksen saamiseksi. Se käyttää operaattoreita kyselyjen suorittamiseen.
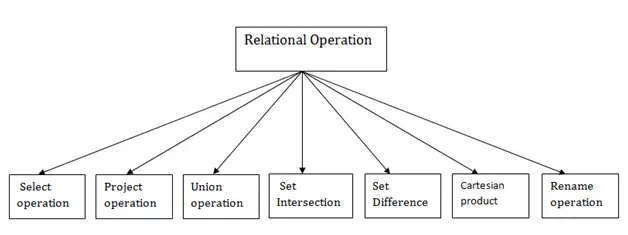
Relaatiotoiminnan tyypit
1. Valitse Käyttö:
- Select-operaatio valitsee monikot, jotka täyttävät tietyn predikaatin.
- Sitä merkitään sigmalla (σ).
Notation: σ p(r)
Missä:
s käytetään valinnan ennustamiseen
r käytetään suhteeseen
s käytetään lauselogiikan kaavana, joka voi käyttää liittimiä, kuten: AND OR ja NOT. Näitä relaatioita voidaan käyttää relaatiooperaattoreina, kuten =, ≠, ≧, , ≦.
Esimerkiksi: LAINA-suhde
| BRANCH_NAME | LAINA_NO | MÄÄRÄ |
|---|---|---|
| Keskusta | L-17 | 1000 |
| Redwood | L-23 | 2000 |
| Perryride | L-15 | 1500 |
| Keskusta | L-14 | 1500 |
| Mianus | L-13 | 500 |
| Roundhill | L-11 | 900 |
| Perryride | L-16 | 1300 |
Syöte:
σ BRANCH_NAME='perryride' (LOAN)
Lähtö:
merkki merkkijonoon javassa
| BRANCH_NAME | LAINA_NO | MÄÄRÄ |
|---|---|---|
| Perryride | L-15 | 1500 |
| Perryride | L-16 | 1300 |
2. Projektin toiminta:
- Tämä toiminto näyttää luettelon niistä määritteistä, jotka haluamme näkyvän tuloksessa. Loput attribuutit poistetaan taulukosta.
- Se on merkitty ∏:llä.
Notation: ∏ A1, A2, An (r)
Missä
A1 , A2 , A3 käytetään suhteen attribuuttinimenä r .
Esimerkki: ASIAKASSUHDE
dhl merkitys
| NIMI | KATTU | KAUPUNKI |
|---|---|---|
| Jones | Main | Harrison |
| Smith | pohjoinen | Ruis |
| Heinää | Main | Harrison |
| Curry | pohjoinen | Ruis |
| Johnson | Sielu | Brooklyn |
| Brooks | Senaattori | Brooklyn |
Syöte:
∏ NAME, CITY (CUSTOMER)
Lähtö:
| NIMI | KAUPUNKI |
|---|---|
| Jones | Harrison |
| Smith | Ruis |
| Heinää | Harrison |
| Curry | Ruis |
| Johnson | Brooklyn |
| Brooks | Brooklyn |
3. Unionin toiminta:
- Oletetaan, että on kaksi monikkoa R ja S. Liitosoperaatio sisältää kaikki monikot, jotka ovat joko R:ssä tai S:ssä tai molemmat R&S:ssä.
- Se poistaa kaksoiskappaleet. Se on merkitty ∪:llä.
Notation: R ∪ S
Ammattiliiton toiminnassa on täytettävä seuraavat ehdot:
- R:n ja S:n attribuutilla on oltava sama numero.
- Kaksoiskappaleet poistetaan automaattisesti.
Esimerkki:
TALLETTAJASUHDE
| ASIAKKAAN NIMI | TILI_NO |
|---|---|
| Johnson | A-101 |
| Smith | A-121 |
| Mayes | A-321 |
| Turner | A-176 |
| Johnson | A-273 |
| Jones | A-472 |
| Lindsay | A-284 |
LAINASUHDE
| ASIAKKAAN NIMI | LAINA_NO |
|---|---|
| Jones | L-17 |
| Smith | L-23 |
| Hayes | L-15 |
| Jackson | L-14 |
| Curry | L-93 |
| Smith | L-11 |
| Williams | L-17 |
Syöte:
poikkeusten käsittely java
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
Lähtö:
| ASIAKKAAN NIMI |
|---|
| Johnson |
| Smith |
| Hayes |
| Turner |
| Jones |
| Lindsay |
| Jackson |
| Curry |
| Williams |
| Mayes |
4. Aseta risteys:
- Oletetaan, että on kaksi monikkoa R ja S. Leikkausoperaatio sisältää kaikki monikot, jotka ovat sekä R&S:ssä.
- Se on merkitty leikkauspisteellä ∩.
Notation: R ∩ S
Esimerkki: Käyttämällä yllä olevaa TALLETTAJA- ja LAINA-taulukkoa
Syöte:
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
Lähtö:
| ASIAKKAAN NIMI |
|---|
| Smith |
| Jones |
5. Aseta ero:
- Oletetaan, että on kaksi monikkoa R ja S. Leikkausoperaatio sisältää kaikki monikot, jotka ovat R:ssä mutta eivät S:ssä.
- Se on merkitty leikkauspisteellä miinus (-).
Notation: R - S
Esimerkki: Käyttämällä yllä olevaa TALLETTAJA- ja LAINA-taulukkoa
Syöte:
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
Lähtö:
osittainen lateksijohdannainen
| ASIAKKAAN NIMI |
|---|
| Jackson |
| Hayes |
| Williams |
| Curry |
6. Karteesinen tuote
- Karteesista tuotetta käytetään yhdistämään yhden taulukon jokainen rivi toisen taulukon jokaisen rivin kanssa. Se tunnetaan myös ristiintuotteena.
- Se on merkitty X:llä.
Notation: E X D
Esimerkki:
TYÖNTEKIJÄ
| EMP_ID | EMP_NAME | EMP_DEPT |
|---|---|---|
| 1 | Smith | A |
| 2 | Harry | C |
| 3 | John | B |
OSASTO
| DEPT_NO | DEPT_NAME |
|---|---|
| A | Markkinointi |
| B | Myynti |
| C | Laillinen |
Syöte:
EMPLOYEE X DEPARTMENT
Lähtö:
| EMP_ID | EMP_NAME | EMP_DEPT | DEPT_NO | DEPT_NAME |
|---|---|---|---|---|
| 1 | Smith | A | A | Markkinointi |
| 1 | Smith | A | B | Myynti |
| 1 | Smith | A | C | Laillinen |
| 2 | Harry | C | A | Markkinointi |
| 2 | Harry | C | B | Myynti |
| 2 | Harry | C | C | Laillinen |
| 3 | John | B | A | Markkinointi |
| 3 | John | B | B | Myynti |
| 3 | John | B | C | Laillinen |
7. Nimeä uudelleen:
Rename-toimintoa käytetään nimeämään uudelleen lähtösuhde. Sitä merkitään rho (p).
Esimerkki: Voimme käyttää uudelleennimeämisoperaattoria nimetäksemme STUDENT-suhteen uudelleen OPISKELIJA1:ksi.
ρ(STUDENT1, STUDENT)
