Prisman pinta-ala: Matematiikassa prisma on monitahoisten perheen olennainen jäsen, ja se määritellään kolmiulotteiseksi muodoksi, jossa on kaksi identtistä monikulmiota vastakkain ja jotka on yhdistetty suorakaiteen tai suunnikkaan muotoisilla sivuilla. Samat monikulmiot voivat olla kolmioita, neliöitä, suorakulmioita, viisikulmioita tai mitä tahansa muuta n-sivuista monikulmiota, ja niitä kutsutaan prisman kannaksi. Prisman muut pinnat ovat suunnikkaat tai suorakulmiot.

Tässä artikkelissa keskustelemme erityyppiset prismat ja prismakaavan pinta-ala, esimerkkejä ja harjoitustehtäviä.

Sisällysluettelo

• Mikä on prisman pinta-ala?
• Erityyppiset prismat
• Kolmisivuinen prisma
• Suorakulmainen prisma
• Neliömäinen prisma
• Viisikulmainen prisma
• Kuusikulmainen prisma
• Prismakaavan pinta-ala
• Prisman pinta-ala Ratkaistu esimerkkejä
• Harjoittele ongelmia prisman pinta-alalla

Mikä on prisman pinta-ala?

Prisman pinta-alaa kutsutaan kokonaispinta-alaksi, jonka kaikki sen pinnat ympäröivät. Prisman pinta-alan määrittämiseksi meidän on laskettava sen jokaisen pinnan pinta-ala ja sitten laskettava tuloksena saadut alueet. Prismassa on kahdenlaisia ​​pinta-aloja, nimittäin sivupinta-ala ja kokonaispinta-ala. Prisman pinta-alaa, lukuun ottamatta kahta yhdensuuntaista pintaa (prisman kantaa), kutsutaan sen sivupinta-alaksi.

Prisman sivupinta-ala = [Peruskehä × korkeus] neliöyksikköä

Nyt prisman kokonaispinta-ala on sen kahden kannan ja sivupinta-alan summa.

Yleinen kaava minkä tahansa tyyppisen oikeanpuoleisen prisman kokonaispinta-alan laskemiseksi on:

Prisman kokonaispinta-ala = [2 (perusala) + (perustan ympärysmitta × korkeus)] neliöyksikköä

Erityyppiset prismat

Prismoja on erilaisia ​​prisman pohjan muodon perusteella, kuten

• Kolmion muotoiset prismat,
• Neliömäiset prismat,
• Suorakaiteen muotoiset prismat,
• Viisikulmaiset prismat,
• Kuusikulmaiset prismat,
• Kahdeksankulmaiset prismat.

Kolmisivuinen prisma

Prismaa, jossa on kolmiopohja, kutsutaan kolmioprismaksi. Kolmion muotoinen prisma koostuu kolmesta kaltevasta suorakaiteen muotoisesta pinnasta ja kahdesta yhdensuuntaisesta kolmion pohjasta. Olkoon H kolmioprisman korkeus; a, b ja c ovat sivujen pituudet ja h on kolmiopohjan korkeus.

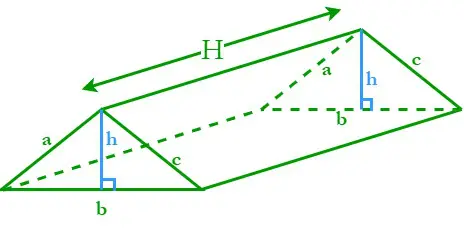
Kolmion pohjan kehä (P) = sen kolmen sivun summa = a + b + c

Kolmion muotoisen pohjan pinta-ala (A) = ½ × kanta × korkeus = ½ bh

Tiedämme, että yleinen kaava Oikean prisman sivupinta-ala on L. S. A. = PH, missä P on peruskehä ja A on kantapinta-ala.

Korvaamalla kaikki yleisen kaavan arvot saamme ,

Kolmioprisman sivupinta-ala = (a + b +c)H neliöyksikköä

missä,

a, b, c ovat kolmion pohjan sivuja

H on kolmioprisman korkeus

Tiedämme, että suoran prisman kokonaispinta-alan yleinen kaava on T. S. A. = PH+2A, missä P on peruskehä, A on kantapinta-ala ja H on prisman korkeus.

Korvaamalla kaikki yleisen kaavan arvot saamme

Kolmion muotoisen prisman kokonaispinta-ala = (a + b + c)H + 2 × (½ bh)

Kolmioprisman kokonaispinta-ala = (a + b + c)H + bh neliöyksikköä

missä,

a, b, c ovat kolmion pohjan sivuja

H on kolmioprisman korkeus

h on kolmion korkeus

Suorakulmainen prisma

Prismaa, jossa on suorakaiteen muotoinen pohja, kutsutaan suorakaiteen muotoiseksi prismaksi. Suorakulmainen prisma koostuu neljästä suorakaiteen muotoisesta pinnasta ja kahdesta yhdensuuntaisesta suorakaiteen muotoisesta alustasta. Olkoon prisman korkeus h ja sen suorakaiteen kannan pituus ja leveys vastaavasti l ja w .

Suorakaiteen muotoisen pohjan kehä (P) = sen neljän sivun summa = 2 (l + w)

Suorakaiteen muotoisen pohjan pinta-ala (A) = pituus × leveys = l × w

Tiedämme, että suoran prisman sivupinta-alan yleinen kaava on L. S. A. = PH, missä P on kantavan kehän ja A on kantavan alueen.

Korvaamalla kaikki yleisen kaavan arvot saamme ,

Suorakaiteen muotoisen prisman sivupinta-ala = 2h(l + w) neliöyksikköä

missä,

l on pituus

w on leveys

h on korkeus

Tiedämme, että yleiskaava suoran prisman kokonaispinta-alalle on T. S. A. = PH+2A, missä P on peruskehä, A on kantapinta-ala ja H on prisman korkeus.

Korvaamalla kaikki yleisen kaavan arvot saamme

Suorakaiteen muotoisen prisman kokonaispinta-ala = 2h(l + w) + 2(l × w)

= 2 lh + 2 wh + 2 lw

Suorakaiteen muotoisen prisman kokonaispinta-ala = 2 (lh + wh + lw) neliöyksikköä

missä,

l on pituus

w on leveys

h on korkeus

Neliömäinen prisma

Prismaa, jossa on neliökanta, kutsutaan neliöprismaksi. Neliömäinen prisma koostuu neljästä suorakaiteen muotoisesta pinnasta ja kahdesta yhdensuuntaisesta neliöpohjasta. Olkoon prisman korkeus h ja sen neliökantojen pituus s.

Neliön pohjan kehä (P) = sen neljän sivun summa = s + s + s + s = 4s

Neliön pohjan pinta-ala (A) = (sivun pituus)²= s²

Tiedämme, että suoran prisman sivupinta-alan yleinen kaava on L. S. A. = PH, missä P on kantavan kehän ja A on kantavan alueen.

Korvaamalla kaikki yleisen kaavan arvot saamme,

Neliöprisman sivupinta-ala = 4sh neliöyksikköä

missä,

s on neliömäisen pohjan puoli

h on neliömäisen prisman korkeus

Tiedämme, että suoran prisman kokonaispinta-alan yleinen kaava on T. S. A. = PH+2A, missä P on peruskehä, A on pohjapinta-ala ja H on prisman korkeus.

Korvaamalla kaikki yleisen kaavan arvot saamme

Neliöprisman kokonaispinta-ala = [4sh + 2s ² ] neliöyksikköä

missä,

s on neliömäisen pohjan puoli

h on neliömäisen prisman korkeus

Viisikulmainen prisma

Prismaa, jossa on viisikulmainen pohja, kutsutaan viisikulmaiseksi prismaksi. Viisikulmainen prisma koostuu viidestä kaltevasta suorakaiteen muotoisesta pinnasta ja kahdesta yhdensuuntaisesta viisikulmaisesta alustasta. Olkoon h viisikulmaisen prisman korkeus; a ja b ovat viisikulmaisten kannan apoteemin pituus ja sivujen pituudet.

Viisikulmion pohjan kehä (P) = sen viiden sivun summa = 5b

Viisikulmion pohjan pinta-ala (A) = 5/2 x (apoteemin pituus) x (sivun pituus) = 5ab

Tiedämme, että suoran prisman sivupinta-alan yleinen kaava on L. S. A. = PH, missä P on kantavan kehän ja A on kantavan alueen.

Korvaamalla kaikki yleisen kaavan arvot saamme,

Viisikulmaisen prisman sivupinta-ala = 5bh neliöyksikköä

missä,

b on viisikulmaisen alustan puoli

h on viisikulmaisen prisman korkeus

Tiedämme, että yleiskaava suoran prisman kokonaispinta-alalle on T. S. A. = PH+2A, missä P on peruskehä, A on kantapinta-ala ja H on prisman korkeus.

Korvaamalla kaikki yleisen kaavan arvot saamme,

Viisikulmaisen prisman kokonaispinta-ala = [5bh + 5ab] neliöyksikköä

missä,

b on viisikulmaisen alustan puoli

a on apoteemin pituus.

h on viisikulmaisen prisman korkeus

Kuusikulmainen prisma

Prismaa, jossa on kuusikulmainen kanta, kutsutaan kuusikulmaiseksi prismaksi. Kuusikulmainen prisma koostuu kuudesta vinosta suorakaiteen muotoisesta pinnasta ja kahdesta yhdensuuntaisesta kuusikulmaisesta alustasta. Olkoon h kuusikulmaisen prisman korkeus; a on kuusikulmioiden sivujen pituudet.

Kuusikulmiopohjan kehä (P) = sen kuuden sivun summa = 6a

Kuusikulmiopohjan pinta-ala (A) = 6 x (tasasivuisen kolmion pinta-ala)

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

Tiedämme, että suoran prisman sivupinta-alan yleinen kaava on L. S. A. = PH, missä P on kantavan kehän ja A on kantavan alueen.

Korvaamalla kaikki yleisen kaavan arvot saamme,

Kuusikulmaisen prisman sivupinta-ala = 6ah neliöyksikköä

missä,

a on kuusikulmaisen pohjan puoli

h on kuusikulmaisen pohjan korkeus

Tiedämme, että yleiskaava suoran prisman kokonaispinta-alalle on T. S. A. = PH+2A, missä P on peruskehä, A on kantapinta-ala ja H on prisman korkeus.

Korvaamalla kaikki yleisen kaavan arvot saamme

Kuusikulmaisen prisman kokonaispinta-ala = [6ah +3√3a²] neliöyksikköä

missä,

a on kuusikulmaisen pohjan puoli

h on kuusikulmaisen pohjan korkeus:

Prismakaavan pinta-ala

Alla oleva taulukko tarjoaa kaavan erityyppisille prismoille:

Prisman pinta-ala Ratkaistu esimerkkejä

Tehtävä 1: Mikä on prisman korkeus, jonka pohjapinta-ala on 36 neliöyksikköä, sen kantakehä on 24 yksikköä ja sen kokonaispinta-ala on 320 neliöyksikköä?

Ratkaisu:

Annetut tiedot,

Pohjapinta-ala = 36 neliöyksikköä

Pohjan ympärysmitta = 24 yksikköä

Prisman kokonaispinta-ala = 320 neliöyksikköä

Meillä on,

Prisman kokonaispinta-ala = (2 × pohjapinta-ala) + (pohjakehä × korkeus)

⇒ 320 = (2 × 36)+ (24 × h)

⇒ 24h = 248 ⇒ h = 10,34 yksikköä

ilmainen ipconfig

Tästä syystä annetun prisman korkeus on 10,34 yksikköä.

Tehtävä 2: Laske neliömäisen prisman kokonaispinta-ala, jos prisman korkeus on 13 cm ja neliön kannan sivun pituus 4 cm.

Ratkaisu:

Annetut tiedot,

Neliömäisen prisman korkeus (h) = 13 cm

Neliön pohjan sivun pituus (a) = 4 cm

Tiedämme sen,

Neliöprisman kokonaispinta-ala = 2a²+ 4ah

= 2 × (4)²+ 4 × 4 × 13

= 32 + 208 = 240 cm²

Annetun prisman kokonaispinta-ala on siis 240 neliöcm.

Tehtävä 3: Määritä viisikulmaisen prisman kantapituus, jos sen kokonaispinta-ala on 100 neliöyksikköä ja sen korkeus ja apoteemin pituus ovat 8 yksikköä ja 5 yksikköä.

Ratkaisu:

Annetut tiedot,

Viisikulmaisen prisman kokonaispinta-ala = 100 neliöyksikköä

Prisman korkeus (h) = 8 yksikköä

Apoteemin pituus (a) = 5 yksikköä

Tiedämme sen,

Viisikulmaisen prisman kokonaispinta-ala = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b (5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 yksikköä

Näin ollen pohjan pituus on 1,54 yksikköä

Ongelma 4: Määritä suorakaiteen muotoisen prisman korkeus ja suorakaiteen muotoisen prisman kokonaispinta-ala, jos sen sivupinta-ala on 540 cm2 ja pohjan pituus ja leveys 13 cm ja 7 cm.

Ratkaisu:

Annetut tiedot,

Suorakaiteen muotoisen pohjan pituus (l) = 13 cm

Suorakaiteen muotoisen alustan leveys (w) = 7 cm

Prisman sivupinta-ala = 540 neliöcm

Meillä on,

Prisman sivupinta-ala = pohjakehä × korkeus

⇒ 540 = 2 (l + w) h

⇒ 2 (13 + 7) h = 540

⇒ 2 (20) h = 540 ⇒ h = 13,5 cm

Tiedämme sen,

Suorakaiteen muotoisen prisman kokonaispinta-ala = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

= 2 × (91 + 94,5 + 175,5) = 722 neliöcm

Näin ollen annetun suorakaiteen muotoisen prisman korkeus ja kokonaispinta-ala ovat 13,5 cm ja 722 cm2.

Tehtävä 5: Määritä säännöllisen kuusikulmaisen prisman pinta-ala, jos prisman korkeus on 12 tuumaa ja pohjan sivun pituus on 5 tuumaa.

Ratkaisu:

Annetut tiedot,

Prisman korkeus (h) = 12 tuumaa

Alustan sivun pituus (a) = 6 tuumaa

Säännöllisen kuusikulmaisen prisman pinta-ala = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3(5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 neliötuumaa

Näin ollen annetun prisman pinta-ala on 489,9 neliötuumaa.

Tehtävä 6: Laske sivuttais- ja kokonaispinta-ala kolmiomaiselle prismmalle, jonka pohjakehä on 25 tuumaa, kolmion kantapituus ja korkeus on 9 tuumaa ja 10 tuumaa ja prisman korkeus on 14 tuumaa.

Ratkaisu:

Annetut tiedot,

Prisman korkeus (H) = 14 tuumaa

Prisman pohjakehä (P) = 25 tuumaa

Kolmion pohjan pituus = 9 tuumaa

Kolmion korkeus = 10 tuumaa

Tiedämme sen,

Prisman sivupinta-ala = pohjakehä × korkeus

= 25 × 14 = 350 neliömetriä

Kolmiopohjan pinta-ala (A) = ½ × pohja × korkeus = 1/2 × 9 × 10 = 45 neliömetriä

Kolmioprisman kokonaispinta-ala = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 neliömetriä

Tästä syystä prisman sivupinta-ala on 350 neliömetriä ja kokonaispinta-ala 440 neliömetriä.

Harjoittele ongelmia prisman pinta-alalla

1. Annettu suorakaiteen muotoinen prisma, jonka mitat:

• Pituus = 6 cm
• Leveys = 4 cm
• Korkeus = 5 cm

Laske kokonaispinta-ala.

2. Tarkastellaan kolmion muotoista prismaa, jonka mitat:

• Kolmion pohja = 8 cm
• Kolmion korkeus = 6 cm
• Prisman pituus = 10 cm

Etsi kokonaispinta-ala.

3. Määritä säännöllisen viisikulmaisen prisman pinta-ala:

• Pohjan sivun pituus = 7 cm
• Prisman korkeus = 9 cm.

4. Laske kuusikulmaisen prisman pinta-ala seuraavasti:

• Tavallisen kuusikulmaisen alustan sivun pituus = 10 cm
• Prisman korkeus = 12 cm.

Prisman pinta-ala – UKK

Mikä on prisma geometriassa?

Prisma on kolmiulotteinen muoto, jossa on kaksi yhteneväistä yhdensuuntaista kantaa ja suorakaiteen muotoiset tai suunnikkaat sivupinnat, jotka yhdistävät niitä. Prismoja on eri muodoissa, kuten suorakaiteen muotoisia prismoja, kolmiomaisia ​​prismoja ja viisikulmaisia ​​prismoja, joilla jokaisella on ainutlaatuiset ominaisuudet.

Kuinka löydät prisman pinta-alan?

Saadaksesi prisman pinta-alan laskemalla sen kaikkien pintojen pinta-alat ja laskemalla ne yhteen. Suorakaiteen muotoisen prisman pinta-alakaava on 2lw + 2lh + 2wh, missä l on pituus, w on leveys ja h on korkeus. Muuntyyppisille prismoille, kuten kolmio- tai viisikulmaisille prismille, voidaan tarvita lisäkaavoja perus- ja sivupinta-alalle.

Mitkä ovat prisman ominaisuudet?

Prismoilla on useita keskeisiä ominaisuuksia:

• Niissä on kaksi samansuuntaista kantaa.
• Sivupinnat ovat kaikki suunnikkaat.
• Korkeus (korkeus) on kohtisuora etäisyys kahden tukikohdan välillä.
• Pohjat ovat muodoltaan ja kooltaan samanlaiset.
• Pohjien suuntainen poikkileikkaus on aina saman muotoinen ja kokoinen kuin alustat.

Mitkä ovat tosielämän esimerkkejä prismoista?

Prismoja löytyy erilaisista jokapäiväisistä esineistä ja rakenteista. Esimerkkejä:

• Suorakaiteen muotoiset prismat: rakennukset, viljalaatikot, kirjat.
• Kolmion muotoiset prismat: Talojen katot, kiilan muotoiset esineet.
• Viisikulmaiset prismat: tietyntyyppiset pylväät, tietyt arkkitehtoniset rakenteet.
• Kuusikulmaiset prismat: Tietyntyyppiset kiteet, jotkut pakkaussäiliöt.

Miksi pinta-ala on tärkeä prismoissa?

Pinta-ala on prismoissa ratkaiseva, koska se edustaa prisman kaikkien pintojen (pintojen) kokonaispinta-alaa. Pinta-alan ymmärtäminen auttaa erilaisissa käytännön sovelluksissa, kuten prisman muotoisen esineen rakentamiseen tai peittämiseen tarvittavan materiaalimäärän laskemisessa, lämmönsiirtonopeuksien määrittämisessä ja pakkaussuunnittelun optimoinnissa.