Kolme ulottuvuutta, pituus, leveys ja korkeus, voidaan mitata mille tahansa kohteelle, jonka voit nähdä tai koskettaa. Kotimme, jossa elämme, on tietyt mitat. Tarkastelemasi suorakaiteen muotoinen näyttö/monitori on pituudeltaan leveä ja leveä. Jokaiselle kolmiulotteiselle geometriselle rakenteelle mitataan pinta-ala ja tilavuus.
Esineen pinnan peittämä ilma on minkä tahansa kohteen pinta-ala. Kohteessa käytettävissä olevan tilan määrä on tilavuus.
Sisällysluettelo
- Pinta-ala
- Kokonaispinta-ala
- Kaareva pinta-ala/sivupinta-ala
- Äänenvoimakkuus
- Esimerkkejä pinta-aloista ja tilavuuksista
- Usein kysytyt kysymykset pinta-ala- ja tilavuuskaavoista
Pinta-ala
Pinta-ala ja tilavuus voidaan laskea mille tahansa kolmiulotteiselle (3D) geometriselle muodolle. Minkä tahansa alueen pinta on alue, jolla kohteen pinta on käytössä. Tilavuus on objektissa käytettävissä olevan tilan määrä. Meillä on erilaisia muotoja, kuten puolipallo, pallo, kuutio, kuutio, sylinteri jne. Kaikilla kolmiulotteisilla muodoilla on pinta-ala ja tilavuus. Mutta kaksiulotteiset muodot, kuten neliöt, suorakulmiot, kolmiot, ympyrät jne.
Tässä kaksiulotteisesti voimme mitata vain alueen. Kolmiulotteisen esineen ulkopinnalla olevaa aluetta kutsutaan pinta-alaksi. Se mitataan neliöyksiköissä.
Aluetta on kahta tyyppiä:
- Kokonaispinta-ala
- Kaareva pinta-ala/sivupinta-ala
Kokonaispinta-ala
Pinta-ala, mukaan lukien pohja(t) ja kaareva osa, vastaa kokonaispinta-alaa. Se on kohteen pinnan ympäröimän alueen määrä. Jos lomakkeella on kaareva pohja ja pinta, niin näiden kahden alueen summa olisi kokonaispinta-ala. Kokonaispinta-ala voidaan määritellä kokonaispinta-alaksi, jonka kohteen peittää, mukaan lukien sen pohja sekä kaareva osa. Jos esineellä on sekä pohja - että kaareva pinta - ala , kokonaispinta - ala on yhtä suuri kuin pohja - ja kaarevan alueen summa .
- Kokonaispinta-ala on esineen kokonaispinta-ala.
- Otetaan esimerkiksi kuutio, jossa on 6 pintaa, 12 reunaa ja 8 kärkeä.
Kokonaispinta-ala = pohjapinta-ala + kaareva pinta-ala
java parseint
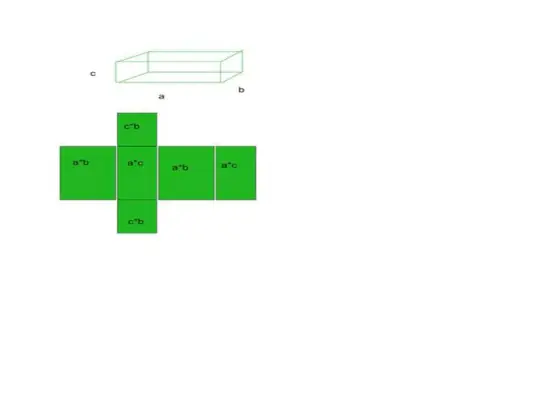
- Kaikkien näiden yhteensä 6 alueen summa on tietyn muodon kokonaispinta-alamme
Esimerkki:
Alla on kulmikas, jonka mitat ovat pituus = 8 cm, leveys = 4 cm ja korkeus = 6 cm, etsi kuution TSA
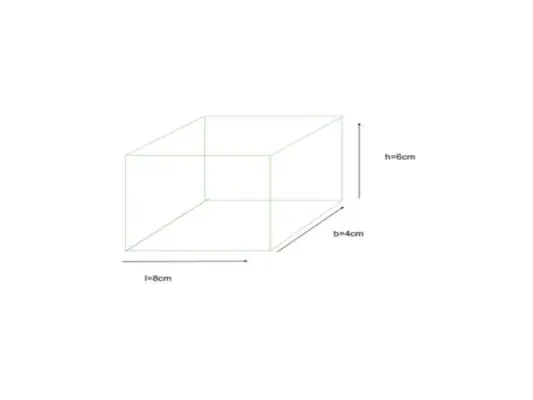
annettu l = 8 cm, b = 4 cm, h = 6 cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
Kuumion TSA on 208 cm.
Kaareva pinta-ala/sivupinta-ala
Kaareva pinta-ala, lukuun ottamatta sen keskustaa, vastaa vain muodon (muotojen) kaarevan osan pinta-alaa. Muodoissa, kuten kartiossa, sitä kutsutaan usein sivupinta-alaksi. Lateraalinen pinta-ala voidaan määritellä alueeksi, joka sisältää vain kohteen kaarevan pinta-alan tai objektin sivupinnan jättämällä pois kohteen pohja-alan. Lateral Surface Area tunnetaan myös kaarevana pinta-alana.
Suurin osa muodoista tai esineistä viittaa kaarevaan pinta-alaan, muoto tai esinemainen sylinteri viittaa siihen lateraalisena pinta-alana. Yksinkertaisesti sanottuna meille näkyvää aluetta kutsutaan sivupinta-alaksi. Harkitse esimerkiksi sylinteriä alla olevan kuvan mukaisesti.
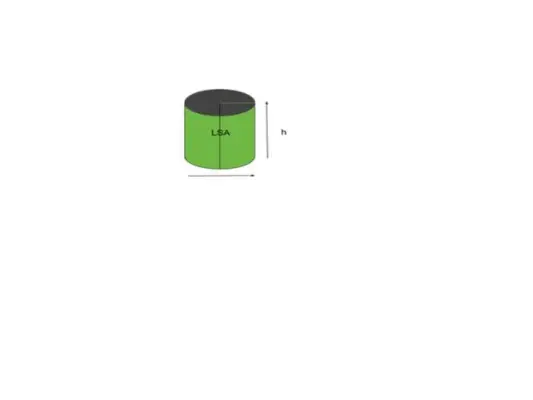
Äänenvoimakkuus
Tilavuus on tilan määrä tietyssä 3D-objektissa. Tilavuuden kokonaismäärää, jonka esine tai aine vie, kutsutaan tilavuudeksi. Se mitataan kuutioyksiköissä.
Pinta-alan ja tilavuuden kaavat
Annettu taulukko sisältää kokonaispinta-alan, kaarevan pinnan/sivupinta-alan ja eri muotojen tilavuuden.
| Muodon nimi | Kaareva pinta-ala | Kokonaispinta-ala | Äänenvoimakkuus |
|---|---|---|---|
| Kuutiomainen | 2h(l + b) | 2 (lb + bh + hl) | l * b * h |
| Kuutio | 4a2 | 6a2 | a3 |
| Sylinteri | 2πrh | 2π(r + h) | πr2h |
| Pallo | 4πr2 merkkijonofunktiot javassa | 4πr2 | 4/3π r3 |
| Kartio | πrl | πr(r + l) | 1/3π r2h |
| Puolipallo | 2pr2 | 3πr2 | 2/3π r3 |
Lue lisää:
- Pyramidin pinta-ala
- Sylinterin pinta-ala
- Puolipallon pinta-ala
- Pallon pinta-ala
- Kuution pinta-ala
Esimerkkejä pinta-aloista ja tilavuuksista
Esimerkki 1: 2 kuutiota, kunkin tilavuus 512 cm 3 yhdistetään päästä päähän. Löytäkää tuloksena olevan kuution pinta-ala?
Ratkaisu:
Annettu,
Kunkin kuution tilavuus (V) = 512 cm3
voimme nyt viitata, että a3= 512 cm3
∴ Kuution sivu, eli a = 8 cm
Nyt tuloksena olevan kuution leveys ja pituus on kumpikin 8 cm, kun taas sen korkeus on 16 cm.
Joten kuution pinta-ala (TSA) = 2 (lb + bh + lh)
Nyt arvot asettamalla saamme
= 2 (8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Näin ollen kuution TSA = 640 cm 2
Esimerkki 2: Meillä on sylinterimäinen kynttilä, halkaisija 14 cm ja pituus 2 cm. Se sulatetaan, jolloin muodostuu kuutiomainen kynttilä, jonka mitat ovat 7 cm × 11 cm × 1 cm. Kuinka monta kuution muotoista kynttilää voi saada?
Ratkaisu:
Sylinterimäisen kynttilän mitat:
Sylinterimäisen kynttilän säde = 14/2 cm = 7 cm
Korkeus/paksuus = 2 cm
Yhden sylinterimäisen kynttilän tilavuus = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Kuution tilavuus kynttilä = 7 x 11 x 1 = 77 cm3
Näin ollen kuution muotoisten kynttilöiden lukumäärä = kuutiokynttilä / yhden sylinterimäisen kynttilän tilavuus = 308/77 = 4
Siten voimme saada 4 kuution muotoista kynttilää.
Esimerkki 3: Nainen haluaa rakentaa savesta pallomaisen lelupallon, jonka säde on yhtä suuri kuin hänen käyttämänsä rannerengas. Koska rannerengas on muodoltaan pyöreä, hän haluaa myös, että rannerengas pinta-ala on yhtä suuri kuin pallon tilavuus. Selvitä hänen kantamansa rannerengas säde?
Ratkaisu:
Olkoon r rannekkeen ja pallon säde,
Meille on annettu, että pallon tilavuus on yhtä suuri kuin rannekkeen pinta-ala:
Siten,
πr2= 4/3 πr3
⇒ r = 3/4
Siksi rannekkeen säde on 3/4 yksikköä.
Esimerkki 4: On annettu, että oikean pyöreän kartion vinon korkeus on 25 cm ja korkeus 24 cm. Löydätkö kartion kaarevan pinnan?
Ratkaisu:
Kartion kaarevan pinta-alan kaava on πrl. Missä r on kartion säde ja l on kartion vinon korkeus.
Tässä kartio on oikea pyöreä kartio.
Kartion säde olisi siis:
r = sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Nyt laskettaessa kaarevaa pintaa ovat:
Vaadittu pinta-ala = (22/7) * 7 * 25 = 550 cm2
instant javaKartion kaareva pinta-ala on siis 550 cm 2 .
Esimerkki 5: Etsi sylinterin sivupinta-ala, jonka pohjan säde on 6 tuumaa ja korkeus 14 tuumaa.
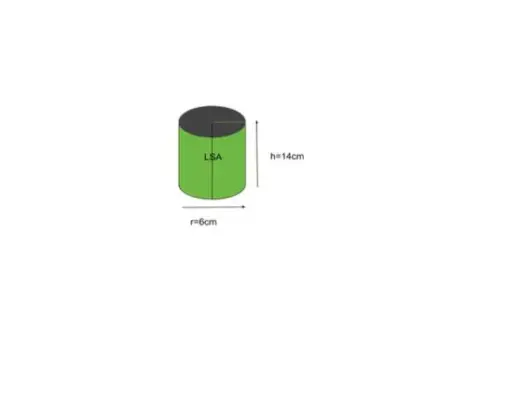
Ratkaisu:
Annettu säde r = 6, korkeus h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527 787
= 528.
Annetun sylinterin LSA on 528 cm .
Harjoittele pinta-aloja ja tilavuuksia koskevia kysymyksiä
Eri Harjoittele pinta-alaa ja tilavuutta koskevia kysymyksiä kaavat ovat:
Q1. Laske kuution pinta-ala, jonka sivun pituus on 5 senttimetriä.
Q2. Laske pallon tilavuus, jonka säde on 3 metriä.
Q3. Määritä sylinterin kokonaispinta-ala, jonka säde on 4 senttimetriä ja korkeus 8 senttimetriä.
Q4. Etsi kartion tilavuus, jonka säde on 6 tuumaa ja korkeus 10 tuumaa.
Q5. Laske pinta-ala suorakaiteen muotoiselle prismmalle, jonka pituus on 7 metriä, leveys 4 metriä ja korkeus 6 metriä.
Usein kysytyt kysymykset pinta-ala- ja tilavuuskaavoista
Mitkä ovat pinta-alan ja tilavuuden kaavat?
Erilaisia pinta-ala- ja tilavuuskaavoja on lisätty yllä olevaan artikkeliin.
Mikä on pinta-alan tilavuuden kaava Luokka 10?
Pinta-alan ja tilavuusluokan 10 kaava sisältää:
| Muodon nimi | Kaareva pinta-ala | Kokonaispinta-ala | Äänenvoimakkuus |
|---|---|---|---|
| Kuutiomainen dfa automata esimerkkejä | 2h(l + b) | 2 (lb + bh + hl) | l × b × h |
| Kuutio | 4a2 | 6a2 | a3 |
| Sylinteri | 2πrh | 2π(r + h) | πr2h |
| Pallo | 4πr2 | 4πr2 | 4/3π r3 |
| Kartio | πrl | πr(r + l) | 1/3π r2h |
| Puolipallo | 2pr2 | 3πr2 | 2/3π r3 |
Mikä on Cuboidin kaava pinta-alalla ja tilavuudella?
- Kuution pinta-ala = 2 (lb + bh + hl)
- Cubiodin tilavuus = l × b × h
Mikä on pinta-ala ja tilavuus?
Pinta-ala on kiinteän aineen kaikkien pintojen pinta-ala ja sen tilavuus on sloidin viemä tila.
