LAISKA CATERIAN ONGELMA

Kun otetaan huomioon kokonaisluku n, joka tarkoittaa pannukakkua, joka voidaan tehdä pannukakkulle, löydä enimmäismäärä kappaleita, jotka voidaan muodostaa tekemällä N -leikkauksia.
Esimerkkejä:

Input : n = 1 Output : 2 With 1 cut we can divide the pancake in 2 pieces Input : 2 Output : 4 With 2 cuts we can divide the pancake in 4 pieces Input : 3 Output : 7 We can divide the pancake in 7 parts with 3 cuts Input : 50 Output : 1276

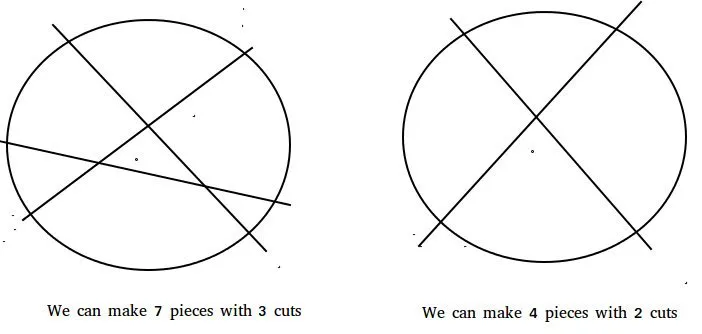
Suositeltu käytäntö Laiska caterian ongelma Kokeile!

Let f(n) denote the maximum number of pieces that can be obtained by making n cuts. Trivially f(0) = 1 As there'd be only 1 piece without any cut. Similarly f(1) = 2 Proceeding in similar fashion we can deduce the recursive nature of the function. The function can be represented recursively as :   f(n) = n + f(n-1)   Hence a simple solution based on the above formula can run in O(n).

Voimme optimoida edellä kaavan.

We now know  f(n) = n + f(n-1) Expanding f(n-1) and so on we have  f(n) = n + n-1 + n-2 + ...... + 1 + f(0) which gives f(n) = (n*(n+1))/2 + 1

Siksi tällä optimoinnilla voimme vastata kaikkiin O (1) -kyselyihin.
Alla on yllä olevan idean toteutus:

C++

// A C++ program to find the solution to // The Lazy Caterer's Problem #include    using namespace std; // This function receives an integer n // and returns the maximum number of // pieces that can be made form pancake // using n cuts int findPieces(int n) {  // Use the formula  return (n * ( n + 1)) / 2 + 1; } // Driver Code int main() {  cout << findPieces(1) << endl;  cout << findPieces(2) << endl;  cout << findPieces(3) << endl;  cout << findPieces(50) << endl;  return 0; }

Java

// Java program to find the solution to // The Lazy Caterer's Problem import java.io.*; class GFG  {  // This function returns the maximum   // number of pieces that can be made  // form pancake using n cuts  static int findPieces(int n)  {  // Use the formula  return (n * (n + 1)) / 2 + 1;  }    // Driver program to test above function  public static void main (String[] args)   {  System.out.println(findPieces(1));  System.out.println(findPieces(2));  System.out.println(findPieces(3));  System.out.println(findPieces(50));  } } // This code is contributed by Pramod Kumar

Python3

# A Python 3 program to  # find the solution to # The Lazy Caterer's Problem # This function receives an  # integer n and returns the  # maximum number of pieces  # that can be made form  # pancake using n cuts def findPieces( n ): # Use the formula return (n * ( n + 1)) // 2 + 1 # Driver Code print(findPieces(1)) print(findPieces(2)) print(findPieces(3)) print(findPieces(50)) # This code is contributed # by ihritik

// C# program to find the solution  // to The Lazy Caterer's Problem using System; class GFG  {  // This function returns the maximum   // number of pieces that can be made  // form pancake using n cuts  static int findPieces(int n)  {  // Use the formula  return (n * (n + 1)) / 2 + 1;  }    // Driver code  public static void Main ()   {  Console.WriteLine(findPieces(1));  Console.WriteLine(findPieces(2));  Console.WriteLine(findPieces(3));  Console.Write(findPieces(50));  } } // This code is contributed by Nitin Mittal.

PHP

 // A php program to find  // the solution to The  // Lazy Caterer's Problem // This function receives  // an integer n and returns  // the maximum number of // pieces that can be made  // form pancake using n cuts function findPieces($n) { // Use the formula return ($n * ( $n + 1)) / 2 + 1; } // Driver Code echo findPieces(1)  'n' ; echo findPieces(2)  'n' ; echo findPieces(3)  'n' ; echo findPieces(50) 'n'; // This code is contributed // by nitin mittal.  ?>

JavaScript

<script> // Javascript program to find the solution to // The Lazy Caterer's Problem  // This function returns the maximum   // number of pieces that can be made  // form pancake using n cuts  function findPieces(n)  {  // Use the formula  return (n * (n + 1)) / 2 + 1;  }   // Driver Code    document.write(findPieces(1) + '  
');  document.write(findPieces(2) + '  
');  document.write(findPieces(3) + '  
');  document.write(findPieces(50));   </script>

Lähtö:

2 4 7 1276

Viitteet: Oeis.org