The Aika monimutkaisuus Yhdistä lajittelu on O(n log n) molemmissa keskiverto ja pahimpia tapauksia . Tilan monimutkaisuus Yhdistä lajittelu On Päällä) . 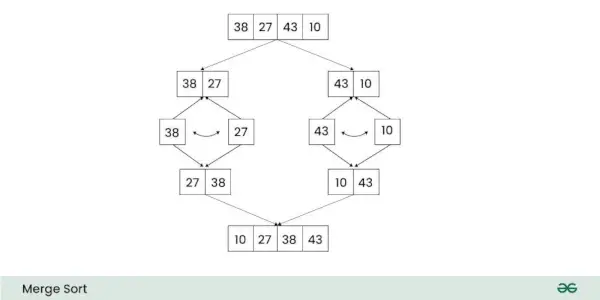
| Aspekti | Monimutkaisuus |
|---|---|
| Aika monimutkaisuus | O(n log n) |
| Avaruuden monimutkaisuus | Päällä) |
Yhdistelmälajittelun aikamonimutkaisuusanalyysi:
Harkitse seuraavia terminologioita:
T(k) = k elementin lajitteluun kulunut aika
M(k) = k elementin yhdistämiseen kulunut aika
Joten se voidaan kirjoittaa
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + vakio * N
Nämä N/2 elementit jaetaan edelleen kahteen puolikkaaseen. Niin,
T(N) = 2 * [2 * T(N/4) + vakio * N/2] + vakio * N
= 4 * T(N/4) + 2 * N * vakio
. . .
= 2k*T(N/2k) + k * N * vakio
Se voidaan jakaa enintään, kunnes yksi elementti on jäljellä. Siis N/2k= 1. k = log 2 N
T(N) = N*T(1) + N*log2N * vakio
= N + N * log2N
Siksi aika monimutkaisuus on O(N * log 2 N) .
Joten parhaassa tapauksessa, pahimmassa tapauksessa ja keskimääräisessä tapauksessa aika monimutkaisuus on sama.
tee javan aikana
Yhdistelmälajittelun tilan monimutkaisuusanalyysi:
Yhdistä lajittelu on a tilan monimutkaisuus / Päällä) . Tämä johtuu siitä, että se käyttää koon ylimääräistä joukkoa n yhdistääksesi syöttötaulukon lajitellut puolikkaat. Aputaulukkoa käytetään yhdistetyn tuloksen tallentamiseen, ja syöttötaulukko korvataan lajitetulla tuloksella.
