Topologinen lajittelu Ohjattu asyklinen kaavio (DAG) on pisteiden lineaarinen järjestys siten, että jokaiselle suunnatulle reunalle u-v on kärkipiste sisään tulee ennen sisään tilauksessa.
Huomautus: Topologinen lajittelu graafille ei ole mahdollista, jos graafi ei ole a PÄIVÄ .
Esimerkki:
lajiteltu arraylist javassa
Suositeltu käytäntöDFS-pohjainen ratkaisu topologisen lajittelun löytämiseen on jo keskusteltu.Syöte: Kaavio:
Esimerkki
Lähtö: 5 4 2 3 1 0
Selitys: Topologisen lajittelun ensimmäinen kärki on aina kärki, jonka in-aste on 0 (piste, jossa ei ole sisääntulevia reunoja). Seuraavan graafin topologinen lajittelu on 5 4 2 3 1 0. Graafilla voi olla useampi kuin yksi topologinen lajittelu. Toinen seuraavan graafin topologinen lajittelu on 4 5 2 3 1 0.
Topologinen järjestys ei välttämättä ole ainutlaatuinen:
Topologinen lajittelu on riippuvuusongelma, jossa yhden tehtävän suorittaminen riippuu useiden muiden tehtävien suorittamisesta, joiden järjestys voi vaihdella. Ymmärretään tämä käsite esimerkin avulla:
Oletetaan, että tehtävämme on saavuttaa koulumme ja päästäksemme sinne, meidän on ensin pukeuduttava. Riippuvuudet vaatteiden käyttämiseen on esitetty alla olevassa riippuvuuskaaviossa. Esimerkiksi kenkiä ei voi käyttää ennen sukkien käyttöä.
Yllä olevasta kuvasta olisit jo ymmärtänyt, että on olemassa useita tapoja pukeutua, alla oleva kuva näyttää joitain niistä.
Voitko luetella kaikki mahdollinen topologinen järjestys pukeutumisesta yllä olevan riippuvuuskaavion mukaan?
Algoritmi topologiselle lajittelulle DFS:n avulla:
Tässä on vaiheittainen algoritmi topologiseen lajitteluun käyttämällä Depth First Searchia (DFS):
- Luo kaavio kanssa n kärjet ja m - suunnatut reunat.
- Alusta pino ja vierailtu kokoinen joukko n .
- Tee seuraavaa jokaiselle kaavion käyttämättömälle pisteelle:
- Kutsu DFS-funktio, jonka kärkipiste on parametrina.
- Merkitse DFS-funktiossa kärkipiste vierailluksi ja kutsu rekursiivisesti DFS-funktiota kaikille vertexin vierailemattomille naapureille.
- Kun kaikki naapurit ovat käyneet, työnnä kärki pinoon.
- Loppujen lopuksi kärkipisteissä on vieraillut, pop elementtejä pinosta ja liitetään tulosluetteloon, kunnes pino on tyhjä.
- Tuloksena oleva lista on graafin topologisesti lajiteltu järjestys.
Kuva Topologinen lajittelualgoritmi:
Alla oleva kuva on esimerkki yllä olevasta lähestymistavasta:

Topologisen lajittelun yleinen työnkulku
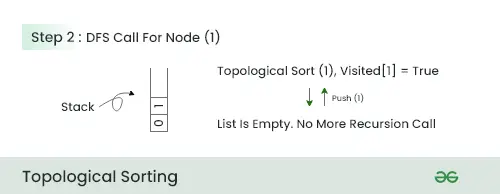
Vaihe 1:
- Aloitamme DFS:n solmusta 0, koska siinä ei ole nollaa saapuvaa solmua
- Työnnämme pinon solmun 0 ja siirrymme seuraavaan solmuun, jossa on vähimmäismäärä vierekkäisiä solmuja, eli solmu 1.
Vaihe 2:
- Tässä vaiheessa, koska tämän solmun vieressä ei ole, työnnä solmu 1 pinossa ja siirry seuraavaan solmuun.
Vaihe 3:
- Tässä vaiheessa valitsemme solmun 2, koska siinä on minimimäärä vierekkäisiä solmuja 0:n ja 1:n jälkeen.
- Kutsumme DFS:ää solmulle 2 ja työnnämme kaikki solmut, jotka tulevat solmusta 2 läpikulkuun, käänteisessä järjestyksessä.
- Paina siis 3 ja sitten 2.
Vaihe 4:
stlc
- Kutsumme nyt DFS:ää solmulle 4
- Koska 0 ja 1 ovat jo olemassa pinossa, joten työnnämme vain solmun 4 pinoon ja palaamme.
Vaihe 5:
- Tässä vaiheessa, koska kaikki 5:n viereiset solmut ovat jo pinossa, työnnämme solmun 5 pinoon ja palaamme.
Vaihe 6: Tämä on Topologisen lajittelun viimeinen vaihe, jossa ponnaamme kaikki elementit pinosta ja tulostamme ne tässä järjestyksessä.
Alla on yllä olevan lähestymistavan toteutus:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, vektori & vieraili, pino & Pino) { // Merkitse nykyinen solmu vierailluksi vierailtu[v] = true; // Toista kaikille vierekkäisille pisteille for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Pino); } // Työnnä nykyinen kärkipiste pinoon, joka tallentaa tuloksen Stack.push(v); } // Topologisen lajittelun suorittava toiminto void topologicalSort(vector>& adj, int V) { pino Pino; // Pinoa tulosvektorin tallentamiseen vieraili(V, false); // Kutsu rekursiivinen apufunktio tallentaaksesi // Topologinen lajittelu alkaen kaikista pisteistä yksitellen // yksi for (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> reunat = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Graafi esitetään vierekkäisyysluettelovektorina> adj(V); for (auto i : reunat) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, boolean[] vieraili, pino pino) { // Merkitse nykyinen solmu vierailluksi vierailluksi[v] = tosi; // Toista kaikille vierekkäisille pisteille for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, vierailtu, pino); } // Työnnä nykyinen kärkipiste pinoon, joka tallentaa // tuloksen pino.push(v); } // Topologisen lajittelun staattisen void topologicalSort(List> adj, int V) { // Pino tallentaaksesi tuloksen Pino pino = new Pino(); boolean[] vieraili = uusi looginen arvo[V]; // Kutsu rekursiivinen apufunktio tallentaaksesi // Topologinen lajittelu alkaen kaikista pisteistä yksitellen // yksitellen for (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> reunat = new ArrayList(); reunat.add(Matriisit.asList(0, 1)); reunat.add(Matriisit.asList(1, 2)); reunat.add(Matriisit.asList(3, 1)); reunat.add(Matriisit.asList(3, 2)); // Graafi esitetään vierekkäisyysluetteloluettelona> adj = uusi ArrayList(V); for (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : reunat) { adj.get(i.get(0)).add(i.get(1)); } topologinen lajittelu(adj, V); } }>
Python 3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] vieraili, pino pino) { // Merkitse nykyinen solmu vierailluksi vierailluksi[v] = tosi; // Toista kaikille vierekkäisille pisteille foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, vierailtu, pino); } // Työnnä nykyinen kärkipiste pinoon, joka tallentaa // tulospinon. Push(v); } // Toiminto topologisen lajittelun suorittamiseksi staattisen void TopologicalSort(List> adj, int V) { // Pino tallentaaksesi tuloksen Pino pino = uusi pino (); bool[] vieraili = uusi bool[V]; // Kutsu rekursiivinen apufunktio tallentaaksesi // Topologinen lajittelu alkaen kaikista pisteistä yksitellen // yksitellen for (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(pino.Pop() + ' '); } } // Ohjainkoodi static void Main(string[] args) { // Solmujen lukumäärä int V = 4; // Edges List> reunat = uusi lista>{ uusi luettelo { 0, 1 }, uusi luettelo { 1, 2 }, uusi luettelo { 3, 1 }, uusi luettelo { 3, 2 } }; // Graafi esitetään vierekkäisyysluetteloluettelona> adj = uusi lista>(); for (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(List i reunoissa) { adj[i[0]].Lisää(i[1]); } Topologinen lajittelu(adj, V); } }>
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { konsoli.loki(pino.pop() + ' '); } } // Ohjainkoodi (() => { // Solmujen lukumäärä const V = 4; // Reunat const reunat = [[0, 1], [1, 2], [3, 1], [3, 2]] // Graafi esitetään vierekkäisyysluettelona const adj = Array.from({ pituus: V }, () => [] for (olkoon i of reunat) { adj[i[0]] (i[1]);>>
Lähtö Topological sorting of the graph: 3 0 1 2>
Aika monimutkaisuus: O(V+E). Yllä oleva algoritmi on yksinkertaisesti DFS ylimääräisellä pinolla. Joten aika monimutkaisuus on sama kuin DFS
Aputila: O(V). Pinoa varten tarvitaan lisätilaa
Topologinen lajittelu BFS:n avulla:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Osoitin taulukkoon, joka sisältää // vierekkäisyysluettelot public: Graph(int V); // Rakentaja void addEdge(int v, int w); // Funktio reunan lisäämiseksi graafiin void topologicalSort(); // tulostaa topologisen lajittelun // koko graafin }; Kaavio::Kaavio(int V) { this->V = V; adj = uusi lista [V]; } void Graph::lisääEdge(int v, int w) { adj[v].push_back(w); // Lisää w v:n luetteloon. } // Topologisen lajittelun suorittava toiminto void Graph::topologicalSort() { // Luo vektori, joka tallentaa kaikkien kärkien vektorien asteen mukaisen in_aste(V, 0); // Läpi viereisyysluettelot täyttääksesi in_degree of // -pisteiden (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; for (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Pura kärjet yksitellen jonosta ja jonosta // vierekkäiset pisteet, jos viereisen in-aste tulee 0:ksi, kun taas (!q.empty()) { // Pura jonon etuosa (tai suorita jonon purku) // ja lisää se topologinen järjestys int u = q.front(); q.pop(); top_order.push_back(u); // Iteroi kaikki sen naapurisolmut // jonosta poistetun solmun u ja pienennä niiden astetta // 1 luettelolla ::iteraattori itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Jos in-aste muuttuu nollaksi, lisää se jonoon if (--in_degree[*itr ] == 0) q.push(*itr); count++; } // Tarkista oliko jakso if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Vierekkäisyysluettelo // graafin // esitys // Rakentaja Graph(int V) { this.V = V; adj = uusi ArrayList[V]; for (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = uusi LinkedList(); for (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = new ArrayList(); // Pura kärkipisteet yksitellen jonosta ja // jonoon vierekkäiset pisteet, jos // viereisen in-aste tulee 0:ksi while (!q.isEmpty()) { // Pura jonon etuosa ja lisää se // topologiseen järjestykseen int u = q.poll(); topOrder.add(u); count++; // Iteroi // puretun solmun u kaikki naapurisolmut ja pienennä niiden astetta // 1:llä for (int w : adj[u]) { // Jos in-aste muuttuu nollaksi, lisää se // jonoon jos (--asteina[w] == 0) q.add(w); } } // Tarkista oliko jakso if (count != V) { System.out.println('Kaavio sisältää syklin'); palata; } // Tulosta topologinen järjestys kohteelle (int i : topOrder) System.out.print(i + ' '); } } // Ohjainkoodi public class Main { public static void main(String[] args) { // Luo yllä olevassa kaaviossa esitetty graafi Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Seuraava on annetun graafin topologinen lajittelu'); g.topologicalSort(); } }> Python 3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Lähtö
Graafin rakentamisen aikamonimutkaisuus on O(V + E), jossa V on kärkien lukumäärä ja E on reunojen lukumäärä.
Topologisen lajittelun aikamonimutkaisuus BFS:llä on myös O(V + E), missä V on kärkien lukumäärä ja E on reunojen lukumäärä. Tämä johtuu siitä, että jokaisessa kärjessä ja jokaisessa reunassa käydään kerran BFS-läpikulun aikana.
muotoile päivämäärä merkkijonoksi
Tilan monimutkaisuus:
Avaruuden monimutkaisuus graafin tallentamiseksi viereisyyslistalla on O(V + E), jossa V on kärkien lukumäärä ja E on reunojen lukumäärä.
Lisätilaa käytetään kärkipisteiden in-aste-asteen tallentamiseen, mikä vaatii O(V)-tilan.
BFS-läpikulkuun käytetään jonoa, joka voi sisältää enintään V-pistettä. Siten jonon tilakompleksisuus on O(V).
Kaiken kaikkiaan algoritmin avaruusmonimutkaisuus on O(V + E) johtuen graafin, asteen taulukon ja jonon tallentamisesta.
Yhteenvetona, tarjotun toteutuksen aikamonimutkaisuus on O(V + E), ja avaruuskompleksisuus on myös O(V + E).
Huomautus: Täällä voimme myös käyttää taulukkoa pinon sijasta. Jos taulukkoa käytetään, tulosta elementit käänteisessä järjestyksessä saadaksesi topologisen lajittelun.
Topologisen lajittelun edut:
- Auttaa ajoittamaan tehtäviä tai tapahtumia riippuvuuksien perusteella.
- Tunnistaa jaksot suunnatussa kaaviossa.
- Tehokas ratkaisemaan ongelmia, joissa on prioriteettirajoituksia.
Topologisen lajittelun haitat:
- Koskee vain suunnattuja asyklisiä kaavioita (DAG), ei sovellu syklisille kaavioille.
- Ei saa olla ainutlaatuinen, kelvollisia topologisia järjestyksiä voi olla useita.
- Tehoton suurille kaavioille, joissa on paljon solmuja ja reunoja.
Topologisen lajittelun sovellukset:
- Tehtävien suunnittelu ja projektinhallinta.
- Riippuvuuden ratkaisu paketinhallintajärjestelmissä.
- Käännösjärjestyksen määrittäminen ohjelmiston rakennusjärjestelmissä.
- Umpikukon havaitseminen käyttöjärjestelmissä.
- Kurssiaikataulut yliopistoissa.
Aiheeseen liittyvät artikkelit:
- Kahnin algoritmi topologiselle lajittelulle
- Kaikki suunnatun asyklisen graafin topologiset tyypit