Prisma on kolmiulotteinen kiinteä hahmo, jolla on kaksi identtistä päätä. Se koostuu litteistä sivuista, samanlaisista alustoista ja yhtäläisistä poikkileikkauksista. Sen pinnat ovat suunnikkaat tai suorakulmiot ilman kantaa. Tällaista prismaa, jossa on kolme suorakaiteen muotoista pintaa ja kaksi yhdensuuntaista kolmion kantaa, kutsutaan kolmiomaiseksi prismaksi. Kolmion muotoiset jalustat on yhdistetty toistensa kanssa yhdensuuntaisilla sivupinnoilla.
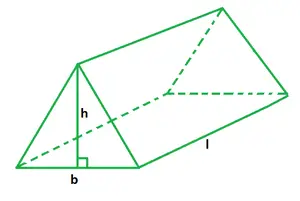
Kolmioprismakaavan tilavuus
Kolmion muotoisen prisman tilavuus määritellään sen sisällä olevaksi tilaksi tai sen täyttämäksi tilaksi. Kolmion muotoisen prisman peruspinta-alan ja korkeuden tunteminen riittää sen tilavuuden laskemiseen. Kolmion muotoisen prisman tilavuus on yhtä suuri kuin pohjan pinta-alan ja prisman korkeuden tulo, joka tunnetaan myös prisman pituutena. Kolmioprisman kantapinta-ala on yhtä suuri kuin puolet kolmion kantan ja sen korkeuden tulosta.
Kaava
V = (1/2) × b × h × l
missä,
b on kolmion kanta,
h on prisman korkeus,
l on prisman pituus.
Esimerkkiongelmat
Tehtävä 1. Etsi kolmion muotoisen prisman tilavuus, jos sen kanta on 6 cm, korkeus 8 cm ja pituus 12 cm.
Ratkaisu:
Meillä on b = 6, h = 8 ja l = 12.
reagoida sisäänrakennettu tyyliKäyttämämme kaava
V = (1/2) × b × h × l
= (1/2) × 6 × 8 × 12
= 3 × 8 × 12
= 288 cu. cm
Tehtävä 2. Etsi kolmion muotoisen prisman tilavuus, jos sen kanta on 5 cm, korkeus 7 cm ja pituus 8 cm.
ketjutus java-merkkijono
Ratkaisu:
Meillä on b = 5, h = 7 ja l = 8.
Käyttämämme kaava
V = (1/2) × b × h × l
= (1/2) × 5 × 7 × 8
= 5 × 7 × 4
= 140 cu. cm
Tehtävä 3. Laske kolmion muotoisen prisman pituus, jos sen kanta on 6 cm, korkeus 9 cm ja tilavuus 98 cu. cm.
Ratkaisu:
Meillä on b = 6, h = 9 ja V = 98.
Käyttämämme kaavalla
V = (1/2) × b × h × l
=> 98 = (1/2) × 6 × 9 × l
java-tyyppinen muuttuja=> 196 = 27 l
=> l = 196/27
=> l = 7,25 cm
Tehtävä 4. Laske kolmioprisman korkeus merenpinnasta, jos sen kanta on 8 cm, pituus 14 cm ja tilavuus 504 cu. cm.
Ratkaisu:
Meillä on b = 8, l = 14 ja V = 504.
Käyttämämme kaavalla
V = (1/2) × b × h × l
=> 504 = (1/2) × 8 × h × 14
=> 504 = 56 tuntia
=> h = 504/56
=> h = 9 cm
Tehtävä 5. Laske kolmioprisman kannan pinta-ala, jos sen pituus on 18 cm, korkeus 10 cm ja tilavuus 450 cu. cm.
Ratkaisu:
Meillä on l = 18, h = 10 ja V = 450.
Käyttämällä tilavuuskaavaa meillä on,
V = (1/2) × b × h × l
=> 450 = (1/2) × b × 10 × 18
=> 450 = 90b
=> b = 450/90
=> b = 5 cm
Näin ollen kolmion pohjan pinta-ala on
tcp ip malliA = (1/2) × b × h
= (1/2) × 5 × 10
= 25 neliöcm
