Matematiikka on kiehtova aine, joka koostuu laajasta valikoimasta käsitteitä ja periaatteita; yksi tällainen käsite on eksponentiaalinen merkintä . Eksponentiaalinen merkintä on peruskäsite, joka sisältää perusluvun nostamisen tiettyyn potenssiin (tai eksponenttiin). Nämä ovat voimakas käsite, jota käytetään ilmaisemaan valtavia ja minimaalisia lukuja sopivammin; Yhtä tällaista esimerkkiä käsitellään tässä artikkelissa, eli 10-5^thTehoa. Joten tässä artikkelissa opimme tuntemaan eksponentiaalisen merkinnän käsitteen, keskustelemme 10:n ja 5:n merkityksestä.^thPower, oppia eri tavoista ilmaista tämä arvo ja keskustella eksponentiaalisen merkinnän sovelluksista eri aloilla kuin matematiikan.

Eksponentiaalisen merkinnän määrittäminen

Eksponentiaalinen tai tieteellinen merkintä on standardoitu ja organisoitu menetelmä lukujen esittämiseen. Se on hyödyllistä, kun käsittelemme suuria ja pieniä lukuja, koska se yksinkertaistaa niiden ilmaisua ja lisää selkeyttä.

Tieteellisen merkinnän osat

Tässä merkinnässä on kaksi osaa:

1. Perusnumero
2. Eksponentti (tai potenssi) numero

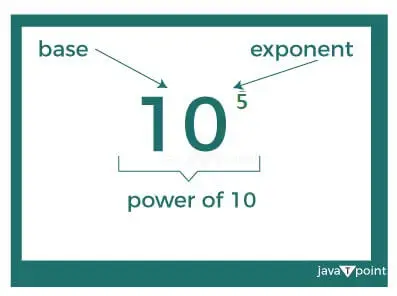
Kantaluku on 10 ja eksponentti 5, mikä osoittaa, kuinka monta kertaa kantaluku (10) kerrotaan itsestään; tämä tarkoittaa sitä 10 5:n potenssiin on 10 kerrottuna itsellään 5 kertaa .

Tarkoittaa 10 x 10 x 10 x 10 x 10 = 10⁵

Ilmaisee 10:stä 5:een^thTehoa

On monia tapoja ilmaista tai edustaa 10:tä 5. tehoon, mikä riippuu myös kentästä, jolla sitä käytetään, tai henkilökohtaisista mieltymyksistä.

Tieteellinen merkintätapa:Yksinkertaisin esitys on 10⁵, jossa 10 on kanta ja 5 on eksponentti tai potenssi; tämä muoto on yleensä ymmärrettävä ja sitä käytetään yleisesti matemaattisessa ja tieteellisessä kirjallisuudessa.Numeerinen esitys:Toinen tapa ilmaista 10 5:n potenssiin on kirjoittaa luku laajennetussa muodossa, 100 000. Tämä muoto jakaa luvun numeroiksi ja korostaa sen suuruutta ymmärtääkseen sen merkityksen.Pitkä lomake:Pitkän muotoinen esitys luvusta 10 5:n tehoon on 'yksi lakh', käytämme tätä muotoa päivittäisessä kielessämme, jotta voimme ymmärtää numeron helpommin.

Merkittävä

10 - 5^thValta on ollut erittäin tärkeä eri aloilla, lähinnä tieteellisessä tutkimuksessa, tekniikassa ja jokapäiväisessä elämässä; se edustaa yhden lakhin arvoa, joka on yhtä suuri kuin 1, jota seuraa viisi nollaa, eli 100 000. Tieteellisissä merkinnöissä tätä arvoa käytetään usein, kun mitataan suuria määriä, kuten planeettojen ja taivaankappaleiden välistä etäisyyttä, lasketaan universumin tähtien lukumäärä ja maailman väestö. Se auttaa tutkijoita ilmaisemaan nämä erittäin suuret määrät helpommin ja helpottaa näiden tietojen ymmärtämistä ja analysointia.

Hakemukset 10-5^thTehoa

Nyt kun ymmärrämme laskelman, tutkitaan joitain käytännön sovelluksia, joissa voimme löytää 10:n ja 5:n osuvuuden.^thTeho:

Digitaalinen tekniikka:Tietokoneissa ja digitaalitekniikassa 10:n tehoilla on merkittävä rooli. Tietokoneet tallentavat ja käsittelevät tietoa binäärikoodilla, joka perustuu kaksinumeroiseen järjestelmään (0 ja 1). Potensseja 2, jotka liittyvät läheisesti potenssiin 10, käytetään kuvaamaan muistikortin kokoa, tiedonsiirtonopeuksia ja prosessorien nopeutta.Väestönkasvu:Eksponentiaalista kasvua havaitaan usein luonnonilmiöissä, mukaan lukien väestönkasvu. Käsite 10-5^thVoima voi auttaa meitä ymmärtämään, kuinka populaatiot voivat kasvaa nopeasti ajan myötä; Jos esimerkiksi 100 000 yksilön populaatio kasvaa 10 % vuodessa, se saavuttaisi noin 14 6410 yksilön neljän vuoden kuluttua.Tieteellinen merkintätapa:10 - 5^thValta on olennainen osa tieteellistä merkintää. Tämä merkintätapa ilmaisee erittäin suuria tai minimaalisia lukuja helpommin hallittavassa muodossa.Mittakaava ja suuruus:Potensseja 10 käytetään usein kuvaamaan esineiden tai ilmiöiden laajuutta tai pienimuotoisuutta. Esimerkiksi tähtitieteilijät käyttävät valovuoden käsitettä, joka on matka, jonka valo kulkee yhdessä vuodessa.Suurien lukujen laskeminen:Aloilla, kuten rahoitus, fysiikka ja tekniikka, käytetään yleensä suuria numeerisia laskelmia. Eksponentiaalinen merkintä on arvokasta näiden laskelmien yksinkertaistamisessa, koska se mahdollistaa kompaktin esityksen ja vähentää virheiden mahdollisuuksia.

Johtopäätös

Eksponenttien ymmärtäminen on olennainen taito ilmaista eri potenssiin korotettuja lukuja. Tässä artikkelissa tutkimme, kuinka ilmaista 10:stä 5:een^thTeho, joka tarkoittaa 10:n kertomista itsellään viisi kertaa; tulos, 100 000, on perusarvo, joka esiintyy eri yhteyksissä, kuten tieteellisessä merkinnässä, muuntoyksiköissä ja binäärilukujärjestelmissä. Omaksumalla eksponentiaalisen merkinnän käsitteen ja sen käytännön sovellukset ymmärrämme paremmin matematiikan Voimaa ja runsautta (läsnäoloa) jokapäiväisessä elämässä.