The XOR tai Exclusive OR Gate on erityinen logiikkaportti, jota käytetään digitaalisessa elektroniikassa yksinomaisen TAI-toiminnon suorittamiseen. XOR-portti ottaa kaksi sisääntuloa ja tuottaa lähdön näiden kahden sisääntulon yhdistelmästä riippuen.

Tässä artikkelissa selitetään kaikki XOR-portin teoria sen mukana totuustaulukko , Boolen lauseke , logiikka symboli , piirikaavio , ja enemmän.

Sisällysluettelo

• Mikä on XOR Gate?
• XOR-portin rakentaminen transistorin avulla
• Ratkaistu esimerkki XOR-portista
• XOR Gaten sovellukset
• Hyödyt ja haitat

Mikä on XOR Gate?

Sisään digitaalinen elektroniikka , on olemassa logiikkapiiri nimeltä XOR Gate, joka ottaa kaksi tuloa ja tuottaa ulostulon, joka on tulojen yhdistelmälle suoritetun yksinomaisen TAI-toiminnon tulos. Tämä logiikkaportti tuottaa korkean tai loogisen 1 -lähdön, kun molemmat tulot ovat erilaisia, muuten se tuottaa loogisen 0-lähdön.

XOR-portin toiminnot

Voimme selittää XOR-portin toiminnan seuraavasti:

Palauttaa 1, jos loogisen korkean tulon määrä on pariton.

merkkijonon muunnos int:ksi javassa

Palauttaa 0, jos loogisen korkean tulon määrä on parillinen.

Oletetaan, että meillä on kaksi tuloa, A ja B ja lähtöä kutsutaan X, niin lauseke on:

XOR-portin Boolen lauseke on seuraava:

merkkijono int javaan

X = A’B + AB’

XOR-portin symboli

XOR-portin logiikkasymboli on esitetty seuraavassa kuvassa. Tässä kuvassa muuttujat A ja B edustavat syöttörivejä ja A'B + AB' on XOR-portin lähtö.

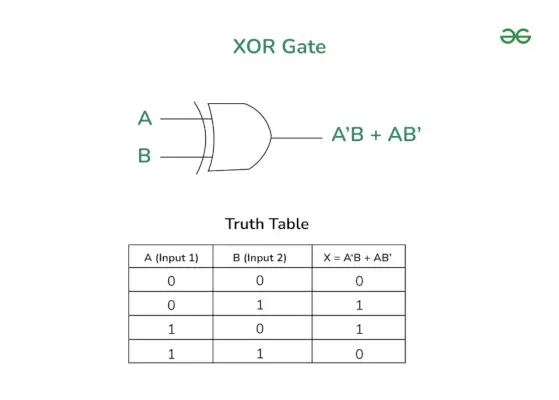
XOR-portin logiikkasymboli ja totuustaulukko

XOR-portin totuustaulukko

XOR-portin totuustaulukko on annettu alla. Tämä taulukko näyttää XOR-portin tulojen ja lähdön välisen suhteen. Tämä antaa myös tietoa XOR-portin toiminnasta eri tuloyhdistelmille.

On tärkeää huomata, että meillä ei ole yhtä XOR-porttia kolmella tai useammalla tulolinjalla. Vain kaksi XOR-tuloporttia on olemassa. Mutta jos tarvitsemme XOR-portin, jossa on enemmän kuin kaksi tulolinjaa, yhdistämme yksinkertaisesti useita kaksituloisia XOR-portteja halutun XOR-portin saamiseksi.

XOR-portin rakentaminen transistorin avulla

Voimme toteuttaa yksinoikeudella TAI portti käyttäen transistoria. Tässä on piiri, joka näyttää eri piirielementtien kytkennän, jotka on yhdistetty toteuttamaan XOR-toiminto.

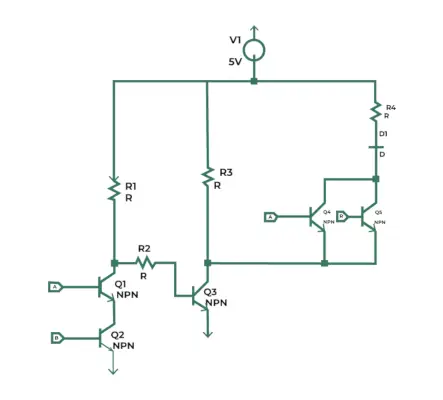
XOR-portti NPN-transistoria käyttäen

Piirin toiminta

Ymmärrämme tämän piirin erilaisten tuloskenaarioiden avulla, kun kyseessä on 2 XOR-tuloportti:

bourne taas shell

TAPAUS I: Kun molemmat tulot ovat nolla. (A=0, B=0)

Kun molemmat tulot A ja B ovat nolla, silloin transistorit Q1, Q2, Q4 ja Q5 ovat avoimet piirit, joten LED ei syty, koska sekä Q4 että Q5 ovat auki, joten LEDin negatiivinen napa ei ole kytketty maahan.

TAPAUS II: Kun yksi tulo, jos looginen korkea ja toinen on loogisesti matala (A=1, B=0)

Tässä tapauksessa voimme helposti nähdä, että Q4 toimii nyt lähipiirinä. Joten LEDin negatiivinen nasta on kytketty Q3:een Q4:n kautta ja lopulta joka on kytketty maahan, joten tässä tapauksessa LED palaa.

TAPAUS III – Kun yksi tulo, jos looginen korkea ja toinen on loogisesti matala (A=0, B=1)

Tässä tapauksessa voimme helposti nähdä, että Q5 toimii nyt lähipiirinä. Joten LEDin negatiivinen nasta on kytketty Q3:een Q5:n kautta ja lopulta joka on kytketty maahan, joten tässä tapauksessa LED palaa.

TAPAUS IV – Kun molemmat tulot ovat loogisesti korkeita. (A=1, B=1)

Tässä tapauksessa, kun sekä A että B ovat loogisesti korkealla, myös transistori Q1 ja Q2 aktivoituvat, virta menee suoraan +5 V liitoksesta maahan Q1- ja Q2-transistoreiden kautta, eikä pääse polulle, johon Q3 on kytketty. tuloksena transistori Q3 toimii nyt avoimena piirinä ja lopulta negatiivisena nastana LED on irrotettu maasta, joten LED ei pala.

sql valitse nimellä

XOR Gaten sovellukset

Tässä on joitain XOR-portin sovelluksia:

1. Tiedonsalaus: XOR-portteja käytetään tietojen salausalgoritmeissa. Koska sitä käytetään yhdistämään tiedot salaiseen avaimeen sen sekoittamiseksi, mikä tekee luvattomien ihmisten murtamisesta erittäin vaikeaa.
2. Vertailupiirit: Sitä käytetään vertailupiirissä tarkistamaan, ovatko kaksi binaariarvoa samat vai eivät. Samantyyppisille tuloille se antaa lähdön 0 ja eri tuloille lähdön 1.
3. Binääri yhteen- ja vähennyslasku: Se auttaa määrittämään kunkin bitin summan ja myös yhdistämään muiden kanssa logiikka portit hoitaa lainatoimintoja.
4. Varvastossut päälle/pois: Sisään T varvastossut se on tottunut piiriin, joka vaihtuu jokaisen ohitetun kellopulssin yhteydessä.

Joitakin muita XOR-porttien käyttötapoja ovat osoitteenpurku, suojaus ja kulunvalvonta, satunnaislukujen luominen, kellon synkronointi , taajuudenjakajapiirit jne.

XOR-portin edut ja haitat

Alla on lista XOR-portin eduista ja haitoista:

XOR Gaten edut

• Se auttaa havaitsemaan, onko syötteiden järjestyksessä pariton määrä '1'.
• XOR-portit suorittavat yksinomaisen TAI-operaation, joka on perustoiminto digitaalista logiikkaa .

XOR Gaten haitat

• XOR-portti on monimutkainen hilapiiri, ja kun se liitetään käytössämme olevaan piiriin, se lisää virrankulutusta ja piirin monimutkaisuutta.
• Se johtaa lisääntymiseen etenemisviive piiristä.
• Tulojen määrän kasvaessa piiri muuttuu yhä monimutkaisemmaksi, mikä vaikeuttaa virheiden ylläpitämistä ja havaitsemista.

Ratkaistu esimerkki XOR-portista

Etsi yksittäinen luku lukusarjasta, koska jokainen elementti esiintyy kahdesti, paitsi tämä yksittäinen elementti.

Ratkaisu: Tiedämme, että kahden saman bitin XOR antaa '0', joten tässä voimme havaita, että jos XOR-kerroimme elementit, jokaisesta kahdesti esiintyvästä elementistä tulee '0' ja vain jäljellä oleva elementti olisi vastauksemme.

Kuten [7,2,2,3,3,4,4,5,5,6,6]

Jos XOR kukin yllä olevista elementeistä, parillisen lukumäärän kertoja esiintyvät elementit antavat '0' ja elementit, jotka esiintyvät parittoman monta kertaa, antavat tulosteen. Lopputuloksena saamme 7, koska vain tämä elementti esiintyy vain kerran ja loput muut elementit esiintyvät parillisen monta kertaa.

Johtopäätös

Tässä artikkelissa olemme oppineet XOR-portista. XOR-portti ottaa Boolen arvot syötteenä ja palauttaa '1', jos loogisen korkean tulon määrä on pariton ja palauttaa 0, jos loogisen korkean tulon määrä on parillinen.

Tämä artikkeli selittää totuustaulukon, symbolisen esityksen, ratkaistun esimerkin ja sovellukset, jotka auttavat ymmärtämään artikkelia paremmin.

XOR Gate – UKK

Onko XOR-portti universaali logiikkaportti?

Ei XOR-portti ei ole universaali logiikkaportti, mutta se voidaan toteuttaa universaalien logiikkaporttien avulla.

Miksi XOR ja XNOR ovat erikoisportteja?

XOR- ja XNOR-portit ovat erityisiä, koska ne suorittaa eksklusiivisia toimintoja välttämättömiä virheiden havaitsemisessa, korjauksessa ja binääriaritmetiikassa, mikä tekee niistä perustavanlaatuisia digitaalisessa logiikassa ja laskennassa.

merkkijono lisäys

Mikä on XOR kahdelle sisääntulolle?

2 sisääntuloa varten, an XOR (yksinomainen OR) portin lähdöt 1 jos ja vain jos toinen tuloista on 1 ja toinen on 0. Jos molemmat tulot ovat samat, lähtö on 0.

Mikä on XOR:n symboli?

Exclusive OR(XOR) -symboli on ⊕.

Voiko XOR:ssa olla 4 tuloa?

Kyllä, XOR-portissa voi olla enemmän kuin kaksi tuloa. Tapauksessa a 4-tuloinen XOR-portti, lähtö on 1, jos pariton määrä tuloja on 1. Jos tulojen 1:iden määrä on parillinen, lähtö on 0.

Voidaanko XOR-portteja käyttää yhteen- ja vähennyslaskuun?

Kyllä, XOR-portteja voidaan käyttää binääriseen yhteen- ja vähennyslaskuun yhdistettynä muihin logiikkaportteihin ja siirtopiireihin. Ne ovat olennaisia ​​komponentteja binääriaritmeettisissa operaatioissa.

Miten XOR-portit käyttäytyvät binäärilogiikan ja totuustaulukoiden suhteen?

XOR-porttien käyttäytyminen on samanlainen kuin binäärilisäys modulo 2 (bittisesti poissulkeva OR), ja niitä käytetään binääritietojen vertailuun ja käsittelyyn.