Z-PISTEET TILASTOISSA

Z-pisteet tilastoissa on mitta siitä, kuinka monta standardipoikkeamaa datapiste on jakauman keskiarvosta. Etsitään z-pisteet tilastoista. Z-pistemäärä 0 osoittaa, että datapisteen pistemäärä on sama kuin keskimääräinen pistemäärä. Positiivinen z-piste osoittaa, että datapiste on keskiarvon yläpuolella, kun taas negatiivinen z-piste osoittaa, että datapiste on keskiarvon alapuolella.

Z-pisteen laskentakaava on: z = (x – μ)/ p

binäärihaku python

Missä:

x: on testiarvo
m: on keskiarvo
osoitteessa: on vakioarvo

Tässä artikkelissa aiomme keskustella seuraavista käsitteistä:

Sisällysluettelo

Mikä on Z-Score?
Kuinka laskea Z-pisteet?
Z-pisteen ominaisuudet
Laske poikkeamat Z-pisteen arvon avulla
Z-Score:n käyttöönotto Pythonissa
Z-pisteen soveltaminen
Z-pisteet vs. keskihajonta
Miksi Z-pisteitä kutsutaan vakiopisteiksi?

Mikä on Z-Score?

Z-piste, joka tunnetaan myös standardipisteenä, kertoo meille datapisteen poikkeaman keskiarvosta ilmaisemalla sen keskihajonnana keskiarvon ylä- tai alapuolella. Se antaa meille käsityksen siitä, kuinka kaukana datapiste on keskiarvosta. Tästä syystä Z-pisteet mitataan keskihajonnan perusteella. Esimerkiksi Z-pisteet 2 osoittaa, että arvo on 2 keskihajonnan päässä keskiarvosta. Z-pisteen käyttämiseksi meidän on tiedettävä väestön keskiarvo (μ) ja myös populaation keskihajonna (σ).

Z-pisteen kaava

Z-pisteet voidaan laskea käyttämällä seuraavaa kaavaa.

z = (X – μ) / p

missä,

z = Z-pisteet
X = Elementin arvo
μ = väestön keskiarvo
σ = väestön keskihajonta

Kuinka laskea Z-pisteet?

Saamme populaation keskiarvon (μ), perusjoukon keskihajonnan (σ) ja havaittu arvo (x) ongelmalausekkeessa korvaamalla saman Z-pisteyhtälössä antaa meille Z-pisteen arvon. Riippuen siitä, onko annettu Z-pistemäärä positiivinen vai negatiivinen, voimme käyttää positiivinen Z-taulukko tai negatiivinen Z-taulukko saatavilla verkossa tai liitteen tilastooppikirjan takana.

Esimerkki 1:

Suoritat GATE-kokeen ja saat pisteet 500. GATE:n keskimääräinen pistemäärä on 390 ja keskihajonta on 45. Kuinka hyvin sait kokeen pisteet keskimääräiseen testin suorittajaan verrattuna?

Ratkaisu:

Seuraavat tiedot ovat helposti saatavilla yllä olevassa kysymyslausekkeessa

Raakapistemäärä/havaittu arvo = X = 500

Keskimääräinen pistemäärä = μ = 390

Keskihajonta = σ = 45

Käyttämällä z-pisteen kaavaa,

z = (X – μ) / p

z = (500 – 390) / 45

z = 110/45 = 2,44

Tämä tarkoittaa, että z-pisteesi on 2.44 .

Koska Z-piste on positiivinen 2,44, käytämme positiivista Z-taulukkoa.

Katsotaanpa nyt Z Taulukko (CC-BY) saadaksesi selville, kuinka hyvin sait pisteitä muihin kokeisiin verrattuna.

Seuraa alla olevia ohjeita löytääksesi todennäköisyys taulukosta.

Tässä, z-pisteet = 2,44, joka i osoittaa, että datapiste on 2,44 standardipoikkeamaa keskiarvon yläpuolella.

Kartoita ensin kaksi ensimmäistä numeroa 2.4 Y-akselilla.
Sitten X-akselia pitkin kartta 0.04
Yhdistä molemmat akselit. Näiden kahden leikkauspiste antaa sinulle kumulatiivisen todennäköisyyden, joka liittyy etsimääsi Z-pistearvoon

[Tämä todennäköisyys edustaa normaalin normaalikäyrän alla olevaa aluetta Z-pisteen vasemmalla puolella]

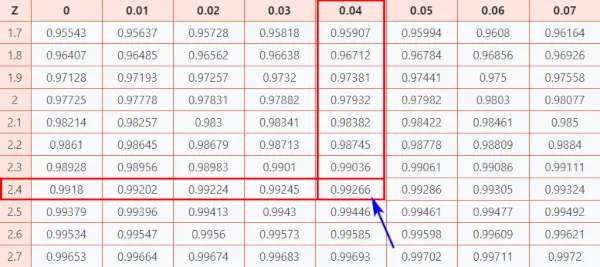
Normaali jakelutaulukko

Tämän seurauksena saat lopullisen arvon, joka on 0,99266 .

Nyt meidän on verrattava alkuperäistä 500-pistettä GATE-tutkimuksessa verrattuna erän keskimääräiseen pistemäärään. Tätä varten meidän on muutettava Z-pisteeseen liittyvä kumulatiivinen todennäköisyys prosenttiarvoksi.

0,99266 × 100 = 99,266 %

Lopuksi voit sanoa, että olet menestynyt hyvin kuin melkein 99 % muista kokeen ottajista.

Esimerkki 2 : Millä todennäköisyydellä opiskelija saa pisteet 350–400 (keskimääräinen pistemäärä μ on 390 ja keskihajonta σ 45)?

Ratkaisu:

Minimipistemäärä = X₁= 350

Maksimipistemäärä = X₂= 400

Käyttämällä z-pisteen kaavaa,

Kanssa₁= (X1 – m) / p

Kanssa₁= (350 – 390) / 45

Kanssa₁= -40 / 45 = -0,88

Kanssa₂= (X₂– m) / s

z2 = (400 – 390) / 45

Kanssa₂= 10/45 = 0,22

Koska z1 on negatiivinen, meidän on tarkasteltava negatiivista Z-pöytä ja huomaa, että kumulatiivinen todennäköisyys p1, ensimmäinen todennäköisyys, on 0,18943 .

Kanssa₂on positiivinen, joten käytämme positiivista Z-taulukkoa, joka antaa kumulatiivisen todennäköisyyden p₂/ 0,58706 .

Lopullinen todennäköisyys lasketaan vähentämällä p1 p:stä₂:
lausunnon tulostaminen javassa

p = p₂– s₁

p = 0,58706 – 0,18943 = 0,39763

Todennäköisyys, että opiskelija saa pisteet 350 ja 400 välillä on 39,763 % (0,39763 * 100).

Z-pisteen ominaisuudet

Z-pisteen suuruus heijastaa sitä, kuinka kaukana datapiste on keskihajonnan keskiarvosta.
Elementti, jonka z-piste on pienempi kuin 0, tarkoittaa, että elementti on pienempi kuin keskiarvo.
Z-pisteet mahdollistavat datapisteiden vertailun eri jakaumista.
Elementti, jonka z-pistemäärä on suurempi kuin 0, tarkoittaa, että elementti on suurempi kuin keskiarvo.
Elementti, jonka z-piste on yhtä suuri kuin 0, edustaa, että elementti on yhtä suuri kuin keskiarvo.
Elementti, jonka z-piste on yhtä suuri kuin 1, edustaa, että elementti on 1 keskihajonnan suurempi kuin keskiarvo; z-piste, joka on yhtä suuri kuin 2, 2 keskihajontaa suurempi kuin keskiarvo ja niin edelleen.
Elementti, jonka z-piste on yhtä suuri kuin -1, edustaa sitä, että elementti on 1 keskihajonnan pienempi kuin keskiarvo; z-piste, joka on yhtä suuri kuin -2, 2 keskihajontaa pienempi kuin keskiarvo ja niin edelleen.
Jos elementtien määrä tietyssä joukossa on suuri, noin 68 %:lla alkioista on z-pisteet välillä -1 ja 1; noin 95 %:lla on z-pisteet välillä -2 ja 2; noin 99 %:lla on z-pisteet välillä -3 ja 3. Tämä tunnetaan empiirisenä sääntönä, ja se ilmaisee datan prosentuaalisen prosenttiosuuden, joka on tietyissä keskipoikkeamissa normaalijakauman keskiarvosta, kuten alla olevassa kuvassa näkyy.

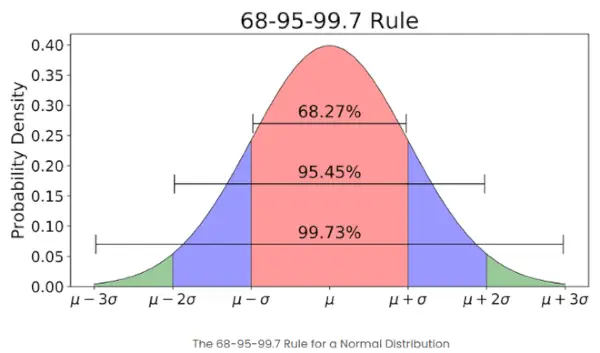
Empiirinen sääntö normaalijakaumassa

Laske poikkeamat Z-pisteen arvon avulla

Voimme laskea poikkeavia tiedoista käyttämällä datapisteiden z-pistearvoa. Vaiheet poikkeavan datapisteen huomioon ottamiseksi ovat seuraavat:

Aluksi keräämme tietojoukon, jossa haluamme nähdä poikkeamat
Laskemme tietojoukon keskiarvon ja keskihajonnan. Näitä arvoja käytetään kunkin datapisteen z-pistearvon laskemiseen.
Laskemme z-pisteen arvon jokaiselle datapisteelle. Z-pisteen arvon laskentakaava on sama kuin
Z = frac{{X – mu}}{{sigma}}
missä X on datapiste, μ on datan keskiarvo ja σ on tietojoukon keskihajonna.
Määritämme z-pisteen raja-arvon, jonka jälkeen datapistettä voidaan pitää poikkeavana arvona. Tämä raja-arvo on hyperparametri, jonka päätämme projektimme mukaan.
Datapiste, jonka z-pistemäärä on suurempi kuin 3, tarkoittaa, että datapiste ei kuulu tietojoukon 99,73 % pisteeseen.
Kaikkia datapisteitä, joiden z-piste on suurempi kuin päättämämme raja-arvo, pidetään poikkeavana arvona.

Tarkistaa: Z-pisteet outlier Detectionille

Z-Score:n käyttöönotto Pythonissa

Pythonilla voimme laskea tietojoukon tietopisteiden z-pistearvon. Lisäksi käytämme numpy-kirjastoa laskeaksemme tietojoukon keskiarvon ja keskihajonnan.

Python 3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Outliers tiedossa on {outliers}')>

Lähtö:

Z-pisteet: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Tietojoukon poikkeamat ovat [150]

java matematiikan luokka

Z-pisteen soveltaminen

Z-pisteitä käytetään usein ominaisuuden skaalaukseen eri ominaisuuksien saattamiseksi yhteiselle mittakaavalle. Ominaisuuksien normalisointi varmistaa, että niillä on nollakeskiarvo ja yksikkövarianssi, mikä voi olla hyödyllistä tietyille koneoppimisalgoritmeille, erityisesti niille, jotka perustuvat etäisyysmittauksiin.
Z-pisteitä voidaan käyttää aineiston poikkeamien tunnistamiseen. Datapisteitä, joiden Z-pisteet ylittävät tietyn kynnyksen (yleensä 3 standardipoikkeamaa keskiarvosta), voidaan pitää poikkeavina.
Z-pisteitä voidaan käyttää poikkeamien havaitsemisalgoritmeissa sellaisten tapausten tunnistamiseen, jotka poikkeavat merkittävästi odotetusta käyttäytymisestä.
Z-pisteitä voidaan soveltaa muuttamaan vääristyneet jakaumat normaalijakaumaksi.
Regressiomallien kanssa työskenneltäessä residuaalien Z-pisteet voidaan analysoida homoskedastisuuden (residuaalien vakiovarianssi) tarkistamiseksi.
Z-pisteitä voidaan käyttää ominaisuuden skaalauksessa tarkastelemalla niiden keskihajontoja keskiarvosta.

Z-pisteet vs. keskihajonta

Z - Pisteet	Standardipoikkeama
Muunna raakadata standardoituun mittakaavaan.	Mittaa vaihtelun tai dispersion määrää arvojoukossa.
Helpottaa eri tietojoukkojen arvojen vertailua, koska ne poistavat alkuperäiset mittayksiköt.	Keskihajonta säilyttää alkuperäiset mittayksiköt, mikä tekee siitä vähemmän sopivan suoriin vertailuihin eri yksiköiden tietojoukkojen välillä.
Ilmoita kuinka kaukana datapiste on keskihajonnan keskiarvosta, mikä mittaa datapisteen suhteellista sijaintia jakaumassa	Ilmaistaan samoissa yksiköissä kuin alkuperäiset tiedot, mikä antaa absoluuttisen mittarin siitä, kuinka jakautuvat arvot ovat keskiarvon ympärillä

Tarkistaa: Z-pisteet taulukko

Miksi Z-pisteitä kutsutaan vakiopisteiksi?

Z-pisteet tunnetaan myös standardipisteinä, koska ne standardoivat satunnaismuuttujan arvon. Tämä tarkoittaa, että standardisoitujen pisteiden luettelon keskiarvo on 0 ja keskihajonta 1,0. Z-pisteet mahdollistavat myös erilaisten muuttujien pisteiden vertailun. Tämä johtuu siitä, että he käyttävät suhteellista asemaa eri muuttujien tai jakaumien tulosten rinnastamiseen.

Z-pisteitä käytetään usein vertaamaan muuttujaa tavalliseen normaalijakaumaan (jossa μ = 0 ja σ = 1).