Polynomin nollat ovat todellisia, kuvitteellisia tai kompleksisia arvoja, kun ne laitetaan polynomiin muuttujan sijasta, tuloksesta tulee nolla (kuten nimi viittaa myös nollaan). Polynomeja käytetään mallintamaan joitain tosielämässä tapahtuvia fyysisiä ilmiöitä, ne ovat erittäin hyödyllisiä tilanteiden matemaattisessa kuvauksessa.

Polynomin nollat ​​ovat kaikki x-arvot, jotka tekevät polynomista nollan. Polynomin nollat ​​kertovat meille polynomin graafin x-leikkauspisteistä. Tässä artikkelissa keskustelemme aiheesta polynomin nollat, kuinka ne löydetään, tekijälause jne.

Sisällysluettelo

• Mitä ovat polynomien nollat?
• Polynomikaavan nollat
• Kuinka löytää polynomin nolla?
• Lineaariselle polynomille
• Quadratic Polynomial
• Kuutiopolynomille
• Tekijälause
• Nollien ja kertoimen välinen suhde
• Nollien ja kertoimen välinen suhde toisen asteen yhtälölle
• Kuutioyhtälön nollien ja kertoimen välinen suhde
• Yhtälön muodostaminen polynomin nollalla
• Nollat ​​polynomikaaviossa
• Lineaarialgebran peruslause
• Juuren moninaisuus
• Polynomin nollia käsitteleviä artikkeleita
• Esimerkkitehtävät polynomin nollasta
• Harjoittele polynomin nollatehtäviä

Mitä ovat polynomien nollat?

Polynomille P(x) sanotaan, että x = a on polynomin nolla, jos P(a) = 0, ja kaikkia sellaisia ​​polynomin nollia kutsutaan yleisesti polynomin nollaksi. Oletetaan esimerkiksi f(x) = 3x – 12. Laita nyt polynomiin x = 4, eli f(4) = 3×4 – 12 = 0. Siten x = 4 on polynomin f( x) = 3x – 12.

Esimerkki: Jos f(x) = x ³ – 6x ² + 11x – 6, onko x = 1 nolla?

Ratkaisu:

Tarkistaa, onko x = 1 nolla f(x) = x:stä³– 6x²+ 11x – 6 tai ei, laita x = 1 in (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 - 6 + 11 - 6 = 12 -12 = 0

Siten x = 1 on f(x:n) nolla.

Polynomikaavan nollat

Lineaariselle polynomille, jonka muoto on ax + b, sen nolla on x = -b/a.

Neliöpolynomille muotoa ax²+ bx + c, sen nolla on x = {- b ± √D}/2a missä D on b:n antama erottelu²– 4ac.

Kuinka löytää polynomin nolla?

Voimme löytää polynomin nollat ​​erityyppisille polynomeille käyttämällä erilaisia ​​menetelmiä, joita käsitellään alla.

• Lineaariselle polynomille
• Quadratic Polynomial
• Kuutiopolynomille

Lineaariselle polynomille

Lineaarisille polynomeille nollan löytäminen on kaikista helpoin. koska nollaa on vain yksi ja se voidaan myös laskea yksinkertaisella polynomin uudelleenjärjestelyllä yhtälöpolynomin jälkeen nollaan.

Etsi esimerkiksi nolla lineaariselle polynomille f(x) = 2x – 7.

Ratkaisu:

Löytääksesi f(x:n) nollan, samasta f(x) arvoon 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Quadratic Polynomial

On olemassa useita menetelmiä toisen asteen polynomin juurien tai nollien löytämiseksi, kuten keskitermin jakaminen, toisen asteen kaava, joka tunnetaan myös Shree Dharacharya -kaavana, ja neliön täydentäminen, joka on jossain määrin samanlainen kuin asteen kaava, koska neliökaava tulee yleisen toisen asteen yhtälön neliön täydentämisestä.

Lisätietoja: toisen asteen yhtälöiden ratkaiseminen tai polynomeja ja kuinka ne ratkaistaan. Seuraavat esimerkit esittävät yksityiskohtaisesti menetelmän neliöpolynomien nollien löytämiseksi.

Esimerkki 1: Selvitä nollat ​​arvolle P(x) = x ² + 2x - 15.

Vastaus:

x²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Esimerkki 2: Selvitä nollat ​​kohteelle P(x) = x ² – 16x + 64.

Vastaus:

x²– 16x + 64 = 0

Verrattuna kirveeseen²+ bx + c = 0,

saamme a = 1, b = -16 ja c = 64.

Täten,

⇒ x = 8, 8

Kuutiopolynomille

Kuutioiden nollien löytämiseksi on monia tapoja, kuten rationaalinen juurilause ja pitkä jako yhdessä. Yksi tapa löytää kuutio- tai minkä tahansa korkeamman asteen polynomin juuret on seuraava:

Vaihe 1: Käytä rationaalisen juurilausetta löytääksesi mahdolliset juuret. eli jos polynomilla on rationaalinen juuri, sen on oltava p/q:n jako, missä p on kokonaislukuvakio ja q on johtava kerroin.

Vaihe 2: Kun olet löytänyt yhden juuren, jaa polynomi sen muodostamalla kertoimella pitkällä jaolla ja kirjoita polynomi osamäärän ja osingon tulona.

Vaihe 3: Jos osamäärä on neliöllinen lauseke, ratkaise se edellä mainituilla menetelmillä neliöpolynomeille. Jos se ei ole asteen 2 polynomi, toista vaiheita 1 ja 2, kunnes osamäärästä tulee polynomi, jonka aste on 2.

Vaihe 4: Vaiheen 3 tulos on vaaditut tekijät, ja vertaamalla tekijä nollaan saadaan polynomin nollat.

Esimerkki: Etsi kuutiopolynomin nollat ​​p(x) = x ³ + 2x ² - 5x - 6.

Ratkaisu:

p(x) = x³+ 2x²- 5x - 6

Koska p/q = -6

Rationaalijuurilauseen mukaan polunomiaalin kaikki mahdolliset rationaaliset juuret ovat p/q:n jakajia.

Siten jakajat = ±1, ±2, ±3, ±6

x = -1, p(x), saamme

p(-1) = (-1)³+ 2 (-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 - 6 = 0

Siten tekijälauseen mukaan x + 1 on p(x) tekijä.

Siten x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Nollalle p(x) = 0,

P(x):n nollat ​​ovat x = -1, x = 2 ja x = -3.

Tekijälause

Polynomille P(x) tekijälause sanoo, että jos x =a on P(X):n nolla, jos x – a on P(x):n tekijä. eli molempien seuraavien ehtojen tulee olla totta.

• Jos a on P(x):n nolla, niin x−a on P(x):n tekijä
• Jos x−a on P(x):n tekijä, niin a on P(x):n nolla

Tämä voidaan varmistaa katsomalla aiempia esimerkkejä. Tekijälause voi johtaa mielenkiintoisiin tuloksiin, jotka ovat seuraavat:

Tulos 1: Jos P(x) on n-asteen polynomi ja r on P(x):n nolla, P(x) voidaan kirjoittaa seuraavassa muodossa:

P(x) = (x – r) Q(x)

Missä Q(x) on n-1-asteinen polynomi ja se saadaan jakamalla P(x) arvolla (x – r).

Tulos 2: Jos P(x) = (x-r)Q(x) ja x = t on Q(x):n nolla, x = t on myös P(x):n nolla.

Varmistaaksesi yllä olevan tosiasian,

Oletetaan, että t on nolla Q(x), mikä tarkoittaa, että Q(t) = 0.

Tiedämme, että r on polynomin P(x) nolla, missä P(x) = (x – r) Q(x),

yritys vs yritys

Joten meidän on tarkistettava, onko x = t myös P(x:n nolla), laitetaan x = t kohtaan P(x)

⇒ P(t) = (t – r) Q(t) = 0

Joten x = t on myös nolla P(x).

Siksi todistettu.

Nollien ja kertoimen välinen suhde

Seuraavassa käsitellään nollien ja neliö- ja kuutioyhtälön kertoimen välistä suhdetta.

Nollien ja kertoimen välinen suhde toisen asteen yhtälölle

Ax-muodon toisen asteen yhtälölle²+ bx + c = 0, jos toisen asteen yhtälön kaksi nollaa ovat α ja β, niin

• Juuren summa = α + β = -b/a
• Juurien tulo = α × β = c/a

Kuutioyhtälön nollien ja kertoimen välinen suhde

Jos α, β ja γ ovat kuutiopolynomin akselin juuri³+ bx²+ cx + d = 0, niin sen nollien ja kertoimien välinen suhde annetaan seuraavasti:

• a + b + c = -b/a
• α × β × γ = -d/a
• αβ + αγ + βγ = c/a

Yhtälön muodostaminen polynomin nollalla

• Neliöpolynomille, jossa on nollia α ja β, neliöpolynomi saadaan kaavalla

x ² – (a + b)x + ab .

• Kuutiopolynomille, jossa on kolme nollaa α, β ja γ, kuutiopolynomi saadaan kaavalla

x ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

Nollat ​​polynomikaaviossa

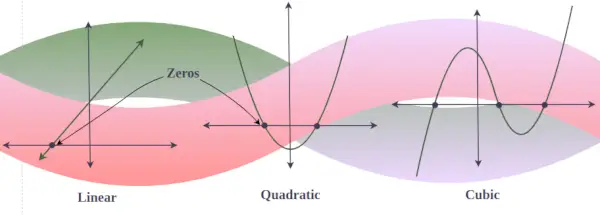
Minkä tahansa polynomin y = f(x) kuvaajassa todelliset nollat ​​ovat piste, jossa kuvaaja leikkaa tai koskettaa x-akselia. (kuten kuvaaja, jossa on kuvitteellinen nolla, ei koskaan leikkaa x-akselia). Toisin sanoen, jos kuutiopolynomilla on 3 todellista ratkaisua, niin tämän kuutiopolynomin kuvaaja leikkaa x-akselin kolme kertaa, mutta jos jollakin kuutiopolynomilla on vain yksi todellinen ratkaisu, niin se kuvaaja leikkaa vain x-akselin kerran.

Lineaarialgebran peruslause

Jos P(x) on n-asteinen polynomi, P(x):ssä on täsmälleen n nollaa, joista osa saattaa toistua.

Tämä tarkoittaa, että jos luetellaan kaikki nollat ​​ja luetellaan jokainen k kertaa, kun k on sen monikerta. Meillä on luettelossa tasan n numeroa. Tämä voi olla hyödyllistä, koska se voi antaa meille käsityksen siitä, kuinka monta nollaa polynomissa pitäisi olla. Joten voimme lopettaa nollien etsimisen, kun saavutamme vaaditun määrän nollia.

Juuren moninaisuus

Oletetaan, että meillä on polynomi P(x) = 0, joka muuttuu

P(x) = (x – r) ^k (x – a) ^m

Jos r on polynomin nolla ja juuren tuottanut eksponentti sen termillä on k, niin sanomme, että r:llä on moninkertaisuus k . Usein kutsutaan nollia, joiden monikertaluku on 1 yksinkertainen nollia ja nollia, joiden monikerta on 2, kutsutaan polynomin kaksoisjuuriksi.

Esimerkki: P(x) on asteen 5 polynomi, joka on kerrottu sinulle. Luettele juuret ja niiden moninaisuus.

P(x) = 5x ⁵ -20x ⁴ +5x ³ +50x ² −20x−40 = 5(x+1) ² (x−2) ³

Ratkaisu:

Annettu, P(x) = 5 (x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Nollien löytämiseksi P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Huomaa, että -1 esiintyy kaksi kertaa nollana, joten sen monikertaisuus on 2, kun taas nollan 2 monikerta on 3.

Polynomin nollia käsitteleviä artikkeleita

• Polynomi
• Toisen yhtälön juuret
• Algebrallinen lauseke

Esimerkkitehtävät polynomin nollasta

Tehtävä 1: Oletetaan, että x = 2 on P(x) = x:n nolla ³ +2x ² −5x−6. Etsi kaksi muuta nollaa.

Ratkaisu:

Aiemmin tutkimastamme peruslauseesta voidaan sanoa, että P(x):ssä on 3 nollaa, koska se on kolmen asteen polynomi. Yksi niistä on x = 2.

Joten voimme kirjoittaa uudelleen P(x),

P(x) = (x – 2) Q(x)

Kahden muun nollan löytämiseksi meidän on selvitettävä Q(x).

Q(x) saadaan jakamalla P(x) luvulla (x-2).

Jakamisen jälkeen Q(x) tulee olemaan

Q(x) = x²+ 4x + 3

Loput kaksi nollaa saadaan selville tästä,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1 (x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Siten kaksi muuta nollaa ovat x = -1 ja x = -3.

Tehtävä 2: Ottaen huomioon, että x = r on polynomin nolla, selvitä polynomin muut nollat.

P(x) = x ³ -6x ² −16x; r = −2

Ratkaisu:

Tiedämme, että x = -2 on nolla,

Joten P(x) voidaan kirjoittaa uudelleen muotoon P(x) = (x + 2) Q(x) {jakoalgoritmin avulla}

Nyt Q(x) löytämiseksi teemme samoin kuin edellisessä kysymyksessä, jaamme P(x):n arvolla (x + 2).

Saamme,

Q(x) = x²– 8x

Nyt löytääksesi kaksi muuta nollaa kertoimella Q(x)

Q(x) = x (x – 8) = 0

Nollat ​​ovat siis x = 0, 8.

Näin ollen meillä on kolme nollaa, x = -2, 0, 8.

Tehtävä 3: Etsi polynomin nollat, 4x ³ -3x ² -25x-6 = 0

Ratkaisu:

Temppu ratkaista polynomiyhtälöitä asteella 3,

Etsi pienin kokonaisluku, joka voi tehdä polynomin arvon 0, alkaa 1,-1,2 ja niin edelleen…

huomaamme, että kun x = -2, lausekkeen arvo on nolla.

Siksi yksi juurista on -2.

Tekijälauseen mukaan jos a on yksi polynomin noloista, niin (x-a) on annetun polynomin tekijä.

Näin ollen tämän jälkeen {x – (-2)} = (x+2) on polynomin yläpuolella oleva tekijä pof.

Saamme toisen asteen yhtälön ja nollia on jo olemassa.

(4x²-11x-3)(x+2) = 0

Kerroin toisen asteen yhtälö,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Tehtävä 4: Etsi polynomin nollat, 4x ⁶ – 16x ⁴ = 0

Ratkaisu:

Polynomilla on aste 6 asti, joten polynomissa on 6 nollaa.

4x⁴(x²-4) = 0

4x⁴(x²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Siksi x = 0, 0, 0, 0, 2, -2

Tehtävä 5: Etsi polynomifunktion f(x) = x nollat ³ – 2x ² – 5x + 6

Ratkaisu:

Tämän polynomin nollien löytämiseksi asetamme f(x) = 0 ja ratkaisemme x:n:

f(x) = x³– 2x²– 5x + 6 = 0

Koska d/a = 6

Rationaalisen juurilauseen mukaan polunomiaalin kaikki mahdolliset rationaaliset juuret ovat

Arvon d/a jakajat = ±1, ±2, ±3, ±6

x = 1, p(x), saamme

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Siten tekijälauseen mukaan x – 1 on p(x) tekijä.

Siten x³+ 2x²– 5x – 6 = (x-1)(x²-x - 6)

x³+ 2x²– 5x – 6 = (x-1) (x+2) (x-3)

Nollalle p(x) = 0,

P(x):n nollat ​​ovat x = 1, x = -2 ja x = 3.

Harjoittele polynomin nollatehtäviä

1. Etsi polynomin f(x) = x kaikki nollat ³ – 6x ² + 11x - 6

2. Määritä polynomin g(x) = 2x kaikki nollat ⁴ – 7x ³ + 3x ² + 4x - 4

3. Etsi polynomin h(x) = x nollat ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Määritä polynomin kaikki nollat p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x - 12.

Usein kysytyt kysymykset nollasta polynomista

Mitä ovat polynomin nollat?

Näistä reaaliarvoista polynomin arvolle tulee 0 eli jos p(x) on polynomi ja p(a) = 0, niin x = a on p(x:n nolla).

Kuinka löytää polynomin nollat?

On olemassa erilaisia ​​​​menetelmiä useille erilaisille polynomeille nollien löytämiseksi, kuten keskimääräisen ja toisen asteen kaava. Lineaarisessa, yksinkertaisessa muuttujien uudelleenjärjestelyssä ja kuutiossa käytämme rationaalisen juurilauseen, pitkän jaon, tekijälauseen ja jäännöslauseen yhdistelmää.

Voiko polynomissa olla enemmän kuin yksi nolla?

Kyllä, polynomissa voi olla enemmän kuin yksi nolla, itse asiassa n asteen polynomissa voi olla enintään n todellista nollaa.

Mikä on polynomin nollan monikerta?

Tekijöintiprosessissa polynomin yksi tekijä tai yksi nolla tuli sitten useita kertoja tekijä tai nolla, jota kutsutaan tuon juuren monikerroksiseksi.

Mikä on algebran peruslause?

Algebran tilojen peruslause Jos P(x) on n-asteinen polynomi, niin P(x):ssä on täsmälleen n nollaa, joista osa saattaa toistua.

Onko polynomilla, jonka tutkinto on n, aina n todellista juuria?

Ei, polynomilla, jonka aste on n, ei aina ole n reaalijuurta, koska jotkut juuret voivat olla imaginaari- tai kompleksilukuja.

Mikä on nollapolynomin aste?

Nollapolynomin aste on nolla.