Kiihtyvyys on nopeuden muutosta ajan myötä. Tosielämän skenaariossa myös kiihtyvyys muuttuu ajan myötä. Esimerkiksi matkustat kaupungista toiseen kaupunkiin maanteitse. Tällöin kiihdytät enemmän, jos tie on tyhjä, ja kiihdyt alas, jos tie on ruuhkaa. Tämä kiihtyvyyden muutos voidaan havaita piirtämällä kiihtyvyys ajan funktiona kaavioon. Tätä kutsutaan kiihtyvyysaikakaavioksi. Tässä artikkelissa opimme yksityiskohtaisesti kiihtyvyysaikakaaviosta ja ratkaisemme ongelmia sen perusteella.

tietokanta

Mikä on kiihtyvyysaikakaavio?

Kiihtyvyys-aikakaaviota käytetään kuvaamaan suhdetta kiihtyvyys ja aika, jossa kiihtyvyys on riippumaton muuttuja, joka on piirretty Y-akselille, ja aika on riippuvainen muuttuja, joka on piirretty X-akselille. Se saadaan, kun saadut kiihtyvyyden ja ajan tiedot piirretään suorakaiteen muotoiseen kuvaajaan tutkittaessa kappaleen liikettä. Voimme määrittää nopeuden muutoksen tietyllä aikavälillä kiihtyvyys-aikakäyrän avulla. Määrittämällä kiihtyvyys-aikakaavion käyrän alla olevan alueen voimme löytää liikkeessä olevan kohteen nopeuden muutoksen tietyn ajanjakson aikana.

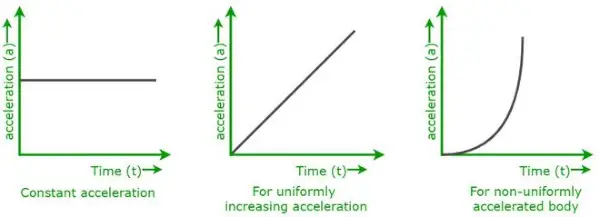
Yllä esitetyt kaaviot ovat kiihtyvyys-aikakaavioita erityyppisille kehon liikkeille.

1. Kun keho liikkuu jatkuvalla kiihtyvyydellä,
2. Kun keho liikkuu tasaisesti kiihtyvyyden kasvaessa.
3. Kun kappale liikkuu epätasaisesti muuttuvalla kiihtyvyydellä.

Johtopäätökset

Seuraavat ovat pisteet, jotka on päätelty kiihtyvyys-aikakaavioista.

• Kiihtyvyys-aikakäyrän kaltevuus on △a/△t.
• Kiihtyvyys-aikakaavion alla oleva alue edustaa nopeuden muutosta.

Antaa,

△ v olla nopeuden muutos,

△a olla muutos kiihtyvyydessä,

△t olla muutos ajassa.

Nyt, käyrän alla oleva pinta-ala = △v

Tiedämme, että kappaleen kiihtyvyyttä kutsutaan nopeuden muutoksen nopeudeksi tietyn ajanjakson aikana.

Niin,

△a = △v/△t

Nyt kertomalla △t:llä molemmilta puolilta saamme

△v = △a × △t (v hich on käyrän alla oleva pinta-ala kiihtyvyysajassa kaavio )

• Objektille, joka liikkuu vakiokiihtyvyydellä, eli kiihtyvyys on sama kaikilla aikaväleillä. Tästä syystä kiihtyvyys-aikakaavion kaltevuus on nolla, ja kuvaaja on yhdensuuntainen aika-akselin kanssa.

Kiihtyvyys vs hidastuminen

Kiihtyvyys: Kappaleen kiihtyvyyttä kutsutaan nopeuden muutoksen nopeudeksi tietyn ajanjakson aikana. Se on vektorisuure ja se mitataan m/s².

Kiihtyvyys = Muutos nopeudessa/ajassa

tässä nopeuden muutos on positiivinen.

Oletetaan, että tasaisella nopeudella liikkuva kappale lisää nopeuttaan. Nopeuden kasvunopeutta kutsutaan kehon kiihtyvyydeksi. Olkoon u alkunopeus, v lopullinen nopeus ja t aikaväli, jolloin kappaleen kiihtyvyys annetaan muodossa,

Kiihtyvyys (a) = (v – u)/t

Esimerkki: Esimerkki kiihtyvyydestä jokapäiväisessä elämässä on auton kääntäminen nurkassa. Auton nopeus kasvaa suunnan vaihtuessa, mikä johtaa kiihtyvyyteen. Kiihtyvyys kasvaa kääntymisnopeuden kasvaessa.

Hidastus: Kehon hidastumista kutsutaan nopeuden muutoksen nopeudeksi tietyn ajanjakson aikana. Hidastus tarkoittaa negatiivista kiihtyvyyttä.

Hidastus = Muutos nopeudessa/ajassa

tässä nopeuden muutos on negatiivinen.

Oletetaan, että kappale, joka kulkee tasaisella nopeudella, pienentää nopeuttaan. Nopeuden alenemisnopeutta kutsutaan kehon hidastumiseksi. Olkoon u alkunopeus, v lopullinen nopeus ja t aikaväli, jolloin kappaleen hidastuminen annetaan seuraavasti,

Hidastus = (v – u)/t

Esimerkki: Tosielämän esimerkki hidastumisesta on tuulettimen sammuttaminen. Kun liikkuvan tuulettimen kytkin kytketään pois päältä, tuulettimen siipien pyörimisnopeus hidastuu asteittain. Tätä puhaltimen nopeuden alenemista kutsutaan hidastumiseksi.

Tarkista myös tämä:

• Etäisyys-aikakaaviot
• Nopeusaikakaaviot

Esimerkkiongelmia kiihtyvyysaikakaavioissa

Tehtävä 1: Määritä nopeuden muutos alla olevasta kiihtyvyys vs. aika -kaaviosta.

Ratkaisu:

Kehon nopeuden muutoksen löytämiseksi meidän on määritettävä käyrän alla oleva pinta-ala.

Joten löytääksemme kohteen nopeuden muutoksen, meidän on laskettava kolmion pinta-ala.

△v = kolmion pinta-ala

= ½ × 25 × 6

△v = 75 m/s.

Näin ollen nopeuden muutos on 75 m/s.

Tehtävä 2: Etsi alla olevasta kiihtyvyys vs aika -kaaviosta kappaleen alkunopeus, jos sen loppunopeus on 55 m/s.

Ratkaisu:

Kehon nopeuden muutoksen löytämiseksi meidän on määritettävä käyrän alla oleva pinta-ala. Kaaviosta voidaan havaita, että siinä on suorakulmio ja kolmio. Joten löytääksemme kohteen nopeuden muutoksen, meidän on laskettava näiden lukujen pinta-ala.

△v = kolmion pinta-ala + suorakulmion pinta-ala

= ½ × 8 × 6 + 2 × 8

△v = 24 + 16 = 42 m/s

Tiedämme sen,

△v = loppunopeus – alkunopeus

42 = 55 – tuumaa_i

sisään_i= 55 – 42 = 13 m/s

Alkunopeus on siis 13 m/s.

Tehtävä 3: Määritä alla olevasta kiihtyvyys vs aika -kaaviosta nopeus kohdassa t = 6 sekuntia, jos v(0) = 0.

Ratkaisu:

Kiihtyvyyden antaa;

a = dv/dt

⇒ dv = (a)dt

Integroimalla molemmin puolin saamme

∫dv = ∫(a) dt

⇒ v = ∫(1.5) dt

⇒ v(t) = 1,5t + c, missä c on vakio

⇒ v(0) = 0

⇒ c = 0

Nyt v(t) = 1,5 t

v(6) = 1,5 × 6 = 9 m/s

Näin ollen nopeus hetkellä t = 6 sek on 9 m/s.

Tehtävä 4: Mitä kiihtyvyys-aikakäyrän alla oleva alue osoittaa?

Ratkaisu:

Kiihtyvyys-aikakaavion alla oleva alue edustaa nopeuden muutosta.

Olkoon △v nopeuden muutos, △a kiihtyvyyden muutos ja △t muutos ajassa.

Nyt käyrän alla oleva pinta-ala = △v

Tiedämme, että kappaleen kiihtyvyyttä kutsutaan nopeuden muutoksen suhteeksi tietyn ajanjakson aikana.

Niin,

△a = △v/△t

Nyt kertomalla △t:llä molemmilta puolilta saamme

△v = △a × △t

Käyrän alla oleva pinta-ala saadaan siis kertomalla kiihtyvyyden muutos ja ajan muutos.

Tehtävä 5: Mitä nykiminen kiihtyvyysaikakaaviossa tarkoittaa?

Ratkaisu:

Nykiminen on äkillinen muutos liikkuvan kappaleen kiihtyvyydessä, ja a-t-käyrän kaltevuus edustaa nykimistä.

Kiihtyvyys-aikakäyrän kaltevuus = nykiminen = △a/△t

Kiihtyvyysaikakaavio – UKK

Mikä on kiihtyvyys-aikakaavio?

Kiihtyvyys-aikakaavio näyttää, kuinka kiihtyvyys vaihtelee ajan kuluessa suoraa linjaa pitkin liikkuvalle objektille. Se piirtää kiihtyvyyden y-akselille ajan funktiona x-akselille.

Kuinka lasket kiihtyvyys-aikakaavion alla olevan alueen ja mitä se edustaa?

Kiihtyvyys-aikakaavion alla oleva alue edustaa nopeuden muutosta kaavion kattaman ajanjakson aikana. Tämän alueen laskemiseksi tyypillisesti lasketaan yhteen käyrän alle mahtuvien suorakulmioiden tai puolisuunnikkaan pinta-alat, jotka vastaavat erillisiä ajanjaksoja, joiden aikana kiihtyvyys on vakio.

Voitko määrittää kohteen nopeuden tiettynä aikana kiihtyvyys-aikakaaviosta?

Hetkellisen nopeuden määrittäminen suoraan tietyllä hetkellä kiihtyvyys-aikakaaviosta ei ole mahdollista. Voit kuitenkin laskea nopeuden muutoksen tietyn ajanjakson aikana etsimällä kaavion alla olevan alueen kyseisen ajanjakson sisällä. Kun tiedät alkunopeuden, voit määrittää lopullisen nopeuden.

Mitä negatiivinen kiihtyvyys ilmaisee tämän tyyppisessä kaaviossa?

Negatiivinen kiihtyvyys kiihtyvyys-aikakaaviossa tarkoittaa hidastuvuutta, jossa kohteen nopeus pienenee, jos kohde liikkuu positiiviseen suuntaan. Jos kohde liikkuu negatiiviseksi katsottuun suuntaan, negatiivinen kiihtyvyys tarkoittaa nopeuden kasvua.

Kuinka voit löytää keskikiihtyvyyden kiihtyvyys-aikakaaviosta?

Keskikiihtyvyys voidaan määrittää etsimällä nopeuden kokonaismuutos (laskemalla yhteen käyrän alla olevat alueet, huomioimalla suunnan) ja jakamalla se kokonaisaikavälillä. Visuaalisesti tämä voidaan esittää suorakulmiona, jonka pinta-ala on yhtä suuri kuin kiihtyvyys-aikakaavion alla oleva kokonaispinta-ala.

Mitä kiihtyvyys-aikakaavion kaltevuus edustaa?

Kiihtyvyys-aikakaavion kaltevuus osoittaa kiihtyvyyden muutosnopeuden ajan kuluessa, mikä tunnetaan nykimisenä. Jyrkkä rinne tarkoittaa nopeaa kiihtyvyyden muutosta.

Kuinka esität levossa olevan kehon kiihtyvyys-aikakaaviossa?

Lepotilassa oleva tai vakionopeudella liikkuva kappale esitetään kiihtyvyys-aikakaaviossa viivalla aika-akselia pitkin nollakiihtyvyydellä.

Miten tulkitset kiihtyvyys-aikakaavion?

Kiihtyvyys-aikakaavion kaltevuus edustaa kiihtyvyyden muutosnopeutta, kun jyrkempi kaltevuus osoittaa suurempaa muutosnopeutta.

Mitä kiihtyvyys-aikakaavion alla oleva alue edustaa?

Käyrän alla oleva pinta-ala kiihtyvyys-aikakaaviossa edustaa kohteen nopeuden muutosta. Tarkemmin sanottuna se edustaa lopullista nopeutta miinus alkunopeus.