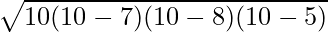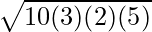Teräväkulmainen kolmio on kolmio, jossa kaikki kolmioiden kulmat ovat teräviä kulmia. Kolmiolla voi olla vain yksi kulma joko suorakulmaisena tai tylpänä kulmana kolmion kulmasummaominaisuuden vuoksi. Ja tästä syystä kolmiota, jossa on kaikki kolme kulmaa terävänä kulmina, eli kulmia, joiden arvo on pienempi kuin 90 astetta, kutsutaan teräväkulmaiseksi kolmioksi.

Kolmion sisäkulmien tyyppien perusteella kolmio voidaan luokitella kolmeen luokkaan: teräväkulmaiset kolmiot, tylpäkulmaiset kolmiot ja suorakulmaiset kolmiot. Otetaan nyt lisätietoja teräväkulmaisista kolmioista, niiden tyypeistä, ominaisuuksista ja muista yksityiskohtaisesti tässä artikkelissa.

Mikä on teräväkulmainen kolmio?

An teräväkulmainen kolmio määritellään kolmioksi, jonka kaikki kolme sisäkulmaa ovat teräviä, eli niiden arvo on välillä 0° - 90°. Kolmion tyypistä riippuen teräväkulmaisen kolmion sivujen pituudet voivat olla yhtä suuria tai eriarvoisia. Teräväkulmainen kolmio seuraa myös kolmion kulman summaominaisuutta.

Alla oleva kuva on teräväkulmainen kolmio, jonka sisäkulmat ovat 45°, 35° ja 80°. Koska kolme sisäkulmaa ovat alle 90°, annettu kolmio on teräväkulmainen kolmio.

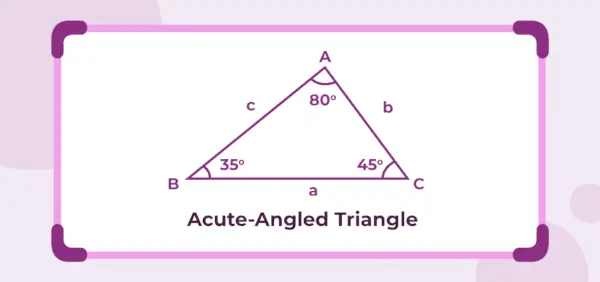
Akuuttikulmaisen kolmion määritelmä

Teräväkulmaiset kolmiot määritellään nimensä mukaisesti kolmioiksi, joissa kolmion kaikki kolme kulmaa ovat teräviä kulmia. Teräväkulmaisten kolmioiden sivu voi olla yhtä suuri tai epätasainen ja sen perusteella ne jaetaan edelleen kolmeen osaan, joita käsitellään alla olevassa artikkelissa,

Teräväkulmaisten kolmioiden tyypit

Teräväkulmaiset kolmiot luokitellaan kolmeen tyyppiin kolmioiden sivujen pituuden mukaan,

• Tasasivuinen terävä kolmio
• Tasakylkinen akuutti kolmio
• Scalene akuutti kolmio

Opitaanpa nyt niistä tarkemmin.

Tasasivuinen terävä kolmio

Tasasivuinen terävä kolmio, jota kutsutaan myös tasasivuiseksi kolmioksi, on kolmio, jossa kaikki kulmat ovat teräviä kulmia ja kaikki kulmat ovat yhtä suuret, myös tasasivuisten terävien kolmioiden sivut ovat yhtä suuret. Tasasivuisen terävän kolmion jokainen kulma on aina 60°.

Tasakylkinen akuutti kolmio

Tasakylkinen terävä kolmio on kolmio, jossa kaikki kulmat ovat teräviä kulmia ja mitkä tahansa kaksi kolmion kulmaa ja näitä kulmia vastaava sivu ovat yhtä suuret. Eli tasakylkisessä terävässä kolmiossa meillä on kaksi sivua ja niitä vastaavat kulmat ovat yhtä suuret.

Scalene akuutti kolmio

Skaalainen terävä kolmio on kolmio, jossa kaikki kulmat ovat teräviä kulmia, eikä kahta kulmaa tai kahta sivua ole yhtä suuri. Toisin sanoen skaalan akuutissa kolmiossa meillä ei ole yhtä suuria sivuja eikä kulmia.

Teräväkulmaisen kolmion ominaisuudet

Seuraavassa on joitain tärkeitä teräväkulmaisen kolmion ominaisuuksia,

• Terävän kulman kolmion sisäkulmat ovat teräviä kulmia, eli kulmat ovat suurempia kuin 0° mutta pienempiä kuin 90°.
• Teräväkulmaisten kolmioiden sisäkulmat seuraavat kulman summaominaisuutta, eli teräväkulmaisen kolmion kulmien summa on 180°.
• Tasasivuinen kolmio on aina teräväkulmainen kolmio, koska tasasivuisen kolmion jokainen sisäkulma on 60°.
• Kolmio ei voi olla samanaikaisesti suorakulmainen kolmio ja teräväkulmainen kolmio.
• Kolmio ei voi olla samanaikaisesti teräväkulmainen kolmio ja tylppäkulmainen kolmio.
• Terävän kulman kolmiossa pienintä kulmaa vastapäätä oleva sivu on pienin ja sen käänteinen on myös tosi.
• Vastaavasti suurinta kulmaa vastapäätä oleva puoli on suurin ja sen käänteinen on myös totta.

Akuuttikulmaiset kolmiokaavat

Pinta-ala ja ympärysmitta ovat kaksi teräväkulmaisen kolmion peruskaavaa, joita käsitellään alla.

kuinka tulostaa java

Teräväkulmaisen kolmion kehä

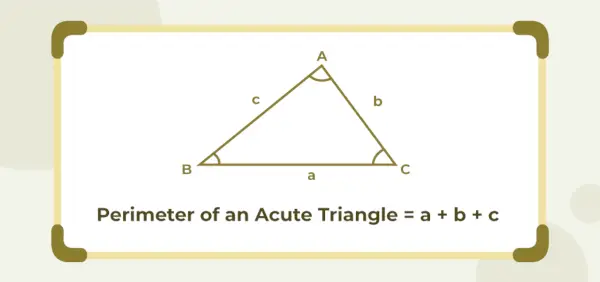
Teräväkulmaisen kolmion ympärysmitta on yhtä suuri kuin sen kolmen sivun pituuden summa. Jos a, b ja c ovat teräväkulmaisen kolmion sivujen pituudet, niin sen ympärysmitta annetaan (a + b + c) -yksiköinä.

Terävän kulman kolmion ympärysmitta = (a + b + c) yksikköä

Missä a , b , ja c ovat kolmion sivujen pituudet.

Lue lisää, Kolmion kehä

Terävän kulman kolmion alue

Kolmion pinta-ala määritellään minkä tahansa kolmion kolmen sivun sulkemaksi kokonaistilaksi kaksiulotteisessa tasossa.

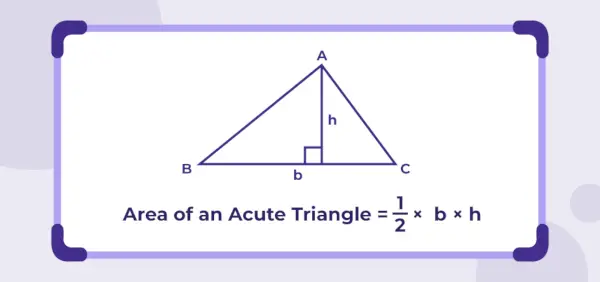
Terävän kulman kolmion pinta-ala = ½ × b × h

Missä,

b on peruspituus ja h on kolmion korkeus.

Lue lisää, Kolmion alue

Akuutti kolmioalue Heronin kaavan mukaan

Jos teräväkulmaisen kolmion kolme sivun pituutta on annettu, niin sen pinta-ala voidaan laskea Heronin kaavalla.

Teräväkulmaisen kolmion pinta-ala =

Missä,

java ohjelmoinnin alkuluvut

s on puolikehä ja s = (a + b + c)/2 , sinä , b , ja c ovat kolmion sivujen pituudet.

Lue lisää, Heronin kaava

Kolmion tärkeät terminologiat

Teräväkulmaiseen kolmioon liittyvät erilaiset terminologiat ovat

Keskustan ympärillä

Ympyrän keskipistettä, joka ohittaa kolmion kolme kärkeä, kutsutaan kolmion ympyrän keskipisteeksi. Se lasketaan ottamalla kohtisuoran puolittajan leikkauspiste. Terävän kulman kolmion ympäryskeskipiste on aina kolmion sisällä.

Incent

Ympyrän keskustaa, joka koskettaa kolmion kolmea sivua, kutsutaan kolmion keskipisteeksi. Se lasketaan ottamalla kulman puolittajan leikkauspiste. Teräväkulmaisen kolmion keskipiste on aina kolmion sisällä.

Keskus

Kolmion mediaanien leikkauskohtaa kutsutaan kolmion sentroidiksi. Teräväkulmaisessa kolmiossa kolmion painopiste on aina kolmion sisällä.

Orthocenter

Kolmion korkeuden leikkauspistettä kutsutaan kolmion ortokeskipisteeksi. Teräväkulmaisessa kolmiossa kolmion ortokeskus on aina kolmion sisällä.

Ratkaistu esimerkkejä teräväkulmaisesta kolmiosta

Esimerkki 1: Mikä seuraavista kulmista voi muodostaa teräväkulmaisen kolmion?

a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°

Ratkaisu:

Tiedämme, että kaikki teräväkulmaisen kolmion kulmat ovat teräviä kulmia, mikä tarkoittaa, että niiden mitta on pienempi kuin 90 astetta.

Ne noudattavat myös kolmion kulmasummaominaisuutta, eli kaikki niiden kulmat summautuvat 180 asteeseen.

a) 65°, 75°, 50°

Tässä kaikki kulmat ovat teräviä kulmia, mutta se ei seuraa kulman summaominaisuutta, joten kolmio ei ole mahdollinen.

65°+ 75°+ 50° = 190° (Kolmio ei mahdollista)

b) 95°, 40°, 45°

Tässä kolmio on mahdollinen, koska se seuraa kolmion kulmien summaa, ts.

95°+ 40°+ 45° = 180

Mutta tarkkaillessamme kolmion kulmia löysimme tylpän kulman 95°. Kolmio ei siis ole teräväkulmainen kolmio.

kokeile tietorakennetta

c) 70°, 40°, 70°

Tässä kolmio on mahdollinen, koska se seuraa kolmion kulmien summaa, ts.

70°+ 40°+ 70° = 180

Ja tarkkaillessamme kolmion kulmia havaitsimme, että kaikki kulmat ovat teräviä kulmia. Kolmio on siis teräväkulmainen kolmio.

d) 90°, 45°, 45°

Tässä kolmio on mahdollinen, koska se seuraa kolmion kulmien summaa, ts.

90°+ 45°+ 45° = 180

Mutta tarkkaillessamme kolmion kulmia löysimme suoran kulman 90°. Kolmio ei siis ole teräväkulmainen kolmio.

Esimerkki 2: Etsi terävän kolmion XYZ kehä, jonka sivut ovat XY = 8 yksikköä, YZ = 5 yksikköä ja XZ = 9 yksikköä.

Ratkaisu:

Annettu,

Terävän kulman kolmion sivut,

• XY(x) = 8 yksikköä
• YZ(y) = 5 yksikköä
• XZ(z) = 9 yksikköä

Tiedämme sen,

Terävän kulman kolmion kehä (P) = x + y + z

⇒ P = (8 + 5 + 9) yksikköä

⇒ P = 22 yksikköä

Näin ollen teräväkulmaisen kolmion ympärysmitta on 22 yksikköä.

Esimerkki 3: Etsi pinta-ala terävälle kolmiolle, jonka korkeus on 12 yksikköä ja kanta on 15 yksikköä.

Ratkaisu:

Annettu,

• Kolmion korkeus (h) = 12 yksikköä
• Kolmion kannan pituus (b) = 15 yksikköä

Tiedämme sen,

Kolmion (A) pinta-ala = ½ × b × h

⇒ A = ½ × 12 × 15

⇒ A = ½ × 180

sql valita useista taulukoista

⇒ A = 90 neliöyksikköä.

Näin ollen annetun terävän kolmion pinta-ala on 90 neliöyksikköä.

Esimerkki 4: Etsi pinta-ala terävälle kolmiolle, jonka sivut ovat AB = 5 cm, BC = 7 cm ja AC = 8 cm.

Ratkaisu:

Annettu,

Terävän kulman kolmion sivut,

• AB = c = 5 yksikköä
• BC = a = 7 yksikköä
• AC = b = 8 yksikköä

Tiedämme sen,

binaarihaku javassa

Kolmion pinta-ala =

⇒ A =

⇒ A =

⇒ A = √(300) neliöcm

⇒ A = 10√3 neliöcm

Näin ollen annetun terävän kolmion pinta-ala on 10√3 neliöcm.

Usein kysytyt kysymykset teräväkulmaisesta kolmiosta

Q1: Mitä ovat akuutit kulmat?

Vastaus:

Kulmaa, joka vaihtelee välillä 0° - 90°, kutsutaan teräväksi kulmaksi. Tämä tarkoittaa, että terävän kulman minimiarvo on suurempi kuin 0° ja terävän kulman maksimiarvo on suurempi kuin 90°.

Q2: Mikä on teräväkulmainen kolmio?

Vastaus:

Teräväkulmainen kolmio on kolmio, jonka kaikki kolme sisäkulmaa ovat teräviä kulmia, eli kulman arvo on välillä 0° - 90°.

Q3: Onko tasasivuinen kolmio aina teräväkulmainen kolmio?

Vastaus:

Kyllä, tasasivuinen kolmio on aina teräväkulmainen kolmio. Teräväkulmaiset kolmiot ovat kulmia, joilla kaikilla kulmilla on terävät kulmat, ja tasasivuisessa kolmiossa kaikki kulmat ovat 60°, eli terävät kulmat. Näin ollen tasasivuinen kolmio on aina teräväkulmainen kolmio.

Q4: Mitkä ovat erityyppiset teräväkulmaiset kolmiot?

Vastaus:

Teräväkulmaiset kolmiot luokitellaan kolmeen tyyppiin, jotka ovat

• Scalene akuutti kolmio
• Tasakylkinen akuutti kolmio
• Tasasivuinen terävä kolmio

K5: Kuinka tietää, onko kolmio teräväkulmainen kolmio?

Vastaus:

Kolmiota, jonka sisäkulmat ovat pienempiä kuin 90°, eli kaikki sisäkulmat ovat teräviä kulmia, niin kolmiota kutsutaan teräväkulmaiseksi kolmioksi. Voimme tarkistaa, onko kolmio teräväkulmainen kolmio yksinkertaisesti tarkkailemalla kolmion kulmia.