Binäärilukujärjestelmä on lukujärjestelmä, jota käytetään esittämään erilaisia lukuja käyttämällä vain kahta symbolia 0 ja 1. Sana binääri on johdettu sanasta bi, joka tarkoittaa kahta. Tästä syystä tätä numerojärjestelmää kutsutaan binäärilukujärjestelmäksi. Näin ollen binäärilukujärjestelmä on järjestelmä, jossa on vain kaksi symbolia.
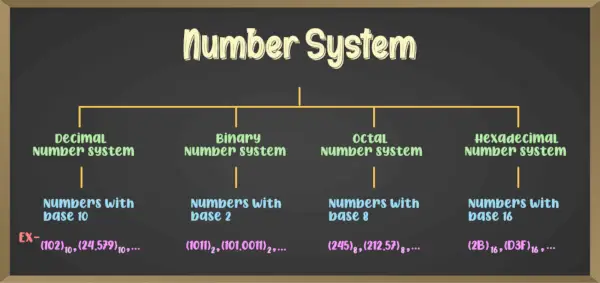
Numerojärjestelmiä on yleensä erilaisia, ja niiden joukossa neljä tärkeintä ovat
- Binäärilukujärjestelmä (numerojärjestelmä, jossa on kanta 2)
- Oktaalilukujärjestelmä (numerojärjestelmä, jossa on kanta 8)
- Desimaalilukujärjestelmä (numerojärjestelmä ja kantaluku 10)
- Heksadesimaalilukujärjestelmä (numerojärjestelmä ja kantaluku 16)
Täällä opimme vain binäärilukujärjestelmästä. Tämä numerojärjestelmä on erittäin hyödyllinen tehtävien selittämisessä tietokoneelle. Binäärilukujärjestelmässä meillä on kaksi tilaa 0 ja 1 ja näitä kahta tilaa edustaa kaksi transistorin tilaa. Jos virta kulkee transistorin läpi, tietokone lukee 1:n ja jos virta puuttuu transistorista, lukee 0. Näin ollen vaihtovirtaa tietokone lukee binäärilukujärjestelmän. Jokaista binäärilukujärjestelmän numeroa kutsutaan bitiksi.
Tässä artikkelissa opimme yksityiskohtaisesti binäärilukujärjestelmästä, binäärilukujärjestelmän muuntamisesta, binääritaulukosta, binäärilukujen toiminnasta, esimerkeistä ja muista.
Sisällysluettelo
- Binäärilukujärjestelmä
- Binäärilukutaulukko
- Binaari-desimaalimuunnos
- Muunnos desimaalista binääriksi
- Binäärilukujen aritmeettiset operaatiot
- Binääriluvun 1:n ja 2:n komplementti
- Binäärilukujärjestelmän käyttötarkoitukset
- Esimerkki binäärilukujärjestelmästä
Binäärilukujärjestelmä
Binäärilukujärjestelmä on numerojärjestelmä, jossa käytämme kahta numeroa 0 ja 1 kaikkien tarvittavien toimintojen suorittamiseen. Binäärilukujärjestelmässä meillä on kantaluku 2. Binäärilukujärjestelmän kantaa kutsutaan myös numerojärjestelmä .
Binäärilukujärjestelmässä edustamme lukua
- (11001)2
Yllä olevassa esimerkissä on annettu binääriluku, jonka kantaluku on 2. Binäärilukujärjestelmässä jokaista numeroa kutsutaan bitiksi. Yllä olevassa esimerkissä on 5 numeroa.
Binäärilukutaulukko
| Desimaaliluku | Binääriluku | Desimaaliluku | Binääriluku |
|---|---|---|---|
| 1 | 001 | yksitoista | 1011 |
| 2 | 010 | 12 globaali var in js | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | viisitoista | 1111 |
| 6 | 110 | 16 | 10 000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 | 1010 | kaksikymmentä | 10100 |
Binaari-desimaalimuunnos
Binääriluku muunnetaan desimaaliluvuksi kertomalla binääriluvun jokainen numero arvon 1 tai 0 potenssilla luvun 2 vastaavaan potenssiin. Otetaan, että binääriluvussa on n numeroa, B = an-1…a3a2a1a0. Nyt vastaava desimaaliluku annetaan muodossa
D = (a n-1 ×2 n-1 ) +…+(a 3 ×2 3 ) + (a 2 ×2 2 ) + (a 1 ×2 1 ) + (a 0 ×2 0 )
Käydään läpi esimerkki ymmärtääksemme käsitettä paremmin.
Esimerkki: Muunna (10011) 2 desimaalin tarkkuudella.
Ratkaisu:
Annettu binääriluku on (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Tästä syystä binääriluku (10011)2ilmaistaan muodossa (19)10.
Muunnos desimaalista binääriksi
Desimaaliluku muunnetaan binääriluvuksi jakamalla annettu desimaaliluku jatkuvasti kahdella, kunnes saamme osamääräksi 1, ja kirjoitamme luvut alaspäin ylöspäin.
Käydään läpi esimerkki ymmärtääksemme käsitettä paremmin.
Esimerkki: Muunna (28) 10 binääriluvuksi.
Ratkaisu:
Siksi (28)10ilmaistaan muodossa (11100)2.
Binäärilukujen aritmeettiset operaatiot
Voimme helposti suorittaa erilaisia toimintoja binääriluvuilla. Erilaisia aritmeettisia operaatioita binääriluvulla ovat mm.
- Binäärilisäys
- Binäärivähennys
- Binäärinen kertolasku
- Binääriosasto
Opitaan nyt samasta yksityiskohtaisesti.
Binäärilisäys
Kahden binääriluvun yhteenlaskettu tulos on myös binääriluku. Kahden binääriluvun yhteenlaskennan tuloksen saamiseksi meidän on lisättävä binäärilukujen numero numero kerrallaan. Alla lisätty taulukko näyttää binäärilisäyksen säännön.
| Binääriluku (1) | Binääriluku (2) | Lisäys | Kanna |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Binäärivähennys
Kahden binääriluvun vähennyksen tulos on myös binääriluku. Kahden binääriluvun vähentämisen tuloksen saamiseksi meidän on vähennettävä binäärilukujen numero numeroittain. Alla lisätty taulukko näyttää binäärivähennyssäännön.
| Binääriluku (1) | Binääriluku (2) | Vähennyslasku | Lainata |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Binäärinen kertolasku
Binäärilukujen kertolasku on samanlainen kuin desimaalilukujen kertolasku. Säännöt minkä tahansa kahden binääriluvun kertomiselle on annettu taulukossa,
| Binääriluku (1) | Binääriluku (2) | Kertominen |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Binääriosasto
The jakomenetelmä binäärilukujen kohdalla on samanlainen kuin desimaalilukujakomenetelmässä. Käydään läpi esimerkki ymmärtääksemme käsitettä paremmin.
Esimerkki: Jaa (101101) 2 kirjoittaja (110) 2
Ratkaisu:
Binääriluvun 1:n ja 2:n komplementti
- Binääriluvun 1:n komplementti saadaan kääntämällä binääriluvun numerot käänteisiksi.
Esimerkki: Etsi luvun 1 komplementti (10011) 2 .
Ratkaisu:
Annettu binääriluku on (10011)2
Nyt, löytääksemme sen 1:n komplementin, meidän on käännettävä annetun luvun numerot.
Näin ollen luvun 1 komplementti (10011)2on (01100)2
- Binääriluvun 2:n komplementti saadaan kääntämällä binääriluvun numerot ja lisäämällä sitten 1 vähiten merkitsevään bittiin.
Esimerkki: Etsi luvun 2 komplementti (1011) 2 .
Ratkaisu:
Annettu binääriluku on (1011)2
Löytääksesi 2:n komplementin, etsi ensin sen 1:n komplementti, eli (0100)2
Nyt lisäämällä 1 vähiten merkitsevään bittiin, saamme (0101)2
Näin ollen 2:n komplementti (1011)2on (0101)2
Binäärilukujärjestelmän käyttötarkoitukset
Binäärilukujärjestelmiä käytetään eri tarkoituksiin ja binäärilukujärjestelmän tärkein käyttötarkoitus on,
- Binäärilukujärjestelmää käytetään kaikessa digitaalielektroniikassa erilaisten toimintojen suorittamiseen.
- Ohjelmointikielet käyttää binaarilukujärjestelmää tietojen koodaamiseen ja dekoodaukseen.
- Binäärilukujärjestelmää käytetään tietotieteissä erilaisiin tarkoituksiin jne.
Lue lisää,
- Binäärikaava
- Ero desimaali- ja binäärilukujärjestelmien välillä
Esimerkki binäärilukujärjestelmästä
Esimerkki 1: Muunna desimaaliluku (98) 10 binaariin.
Ratkaisu:
Näin ollen binääriluku arvolle (98)10on yhtä suuri kuin (1100010)2
Esimerkki 2: Muunna binääriluku (1010101) 2 desimaaliluvuksi.
Ratkaisu:
Annettu binääriluku, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 × 26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Näin ollen binääriluku (1010101)2on yhtä suuri kuin (85)10desimaalijärjestelmässä.
Esimerkki 3: Jaa (11110) 2 kirjoittaja (101) 2
Ratkaisu:
Esimerkki 4: Lisää (11011) 2 ja (10100) 2
Ratkaisu:
Siksi (11011)2+ (10100)2= (101111)2
Esimerkki 5: Vähennä (11010) 2 ja (10110) 2
Ratkaisu:
Siksi (11010)2– (10110)2= (00100)2
Esimerkki 6: Kerro (1110) 2 ja (1001) 2 .
Ratkaisu:
Näin ollen (1110)2× (1001)2= (1111110)2
Binäärilukujärjestelmän usein kysytyt kysymykset
Mikä on binäärilukujärjestelmä?
Binäärilukujärjestelmä on yksi neljästä numerojärjestelmästä, jota käytetään esittämään numeroita käyttämällä vain kahta numeroa, 0 ja 1. Binäärilukujärjestelmässä numeroita kutsutaan 'bitteiksi'. Tietokoneet käyttävät binaarilukujärjestelmää erilaisten laskelmien suorittamiseen.
Mikä on a B se?
Binäärilukujärjestelmässä bitti määritellään yksittäisiksi numeroiksi, joilla on arvo '0' tai '1'.
Mikä on nibble?
Neljän numeron ryhmää kutsutaan Niblleksi.
Mikä on 10:n binääriarvo?
Binääriarvo 10 on (1010)2
Mitkä ovat numerojärjestelmien tyypit?
Numerojärjestelmiä on monenlaisia, ja jotkut niistä ovat
- Binäärilukujärjestelmä
- Oktaalilukujärjestelmä
- Desimaalilukujärjestelmä
- Heksadesimaalilukujärjestelmä
Kuinka laskea binääriluvut?
Binääriluvut lasketaan desimaaliluvuista jakamalla desimaaliluku kahdella ja kirjoittamalla jäännös. Järjestämme sitten kaikki jäännökset uusimmasta vanhimpaan saadaksemme binääriluvun.
Kuinka lisätä binäärilukuja?
Binääriluvut lisätään käyttämällä alla kirjoitettuja kaavoja,
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (kanna 1)






