- Bitwise XOR-operaattori tunnetaan myös nimellä Yksinomainen TAI
- Se on merkitty käyttämällä '^'
- Kuten nimestä käy ilmi, se toimii bitin taso operandeista.
- Bitwise XOR-operaattori on tullut Bitwise-operaattorien luokkaan.
- Bittikohtaisessa poissulkevassa TAI-operaattorissa (XOR) tarvitaan kaksi operandia, ja nämä kaksi operandia erotetaan XOR-symbolilla, eli '^':lla.
- Määrittääksemme lähdön tai tuloksen, joka tulee ulos XOR-operaattorin soveltamisen jälkeen kahdelle operandille, meidän on noudatettava XOR-operaattorin loogista totuustaulukkoa.
- XOR Truth Table on matemaattinen taulukko, joka on rakennettu käyttämällä XOR-operaattorin oikeaa logiikkaa.
- XOR-operaattorin takana käytetty logiikka on; aina kun XOR-toimintoa käytetään molemmissa eri kahden operandin bittiä, niin tulos tuottaa aina '1', ja jos XOR-operaatiota sovelletaan molempiin sama kahden operandin bittiä, niin tulos tuottaa ulostulon '0'.
Exclusive OR (XOR) -operaattorin totuustaulukko
Olkoon kaksi operandia; Ensimmäinen on A ja toinen on B, näiden kahden operandin muodostamien syötteiden kokonaisyhdistelmät ovat 4. Seuraavaa XOR-totuustaulukkoa käyttämällä määritetään vastaava tulos. Tulos tallennetaan C-muodossa, tästä C = A ^ B.
Tässä totuustaulukossa otetaan syöte bittien muodossa, eli 0 ja 1, ja myös ulostulo muodostetaan bittien muodossa, eli 0 ja 1.
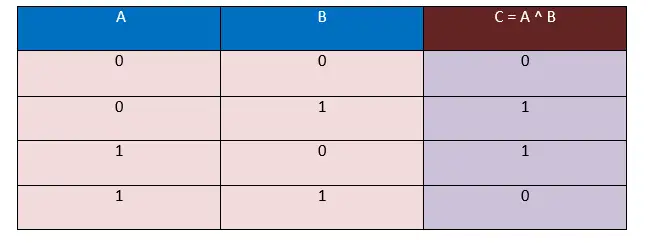
Tässä yllä olevassa XOR Truth -taulukossa havaitaan, että kun operandien A ja B arvot ovat erilaiset, eli ( 0, 1 ), ( 1, 0 ), tulos on aina 1. Ja kun Operandien A ja B arvot ovat samat, eli ( 0, 0 ), ( 1, 1 ), ulos tuleva tulos on aina 0.
Vastaavasti tällä tavalla voimme piirtää totuustaulukon Boolean arvot -
Olkoon kaksi operandia; ensimmäinen on A ja toinen on B . Näiden kahden operandin muodostamien syötteiden kokonaisyhdistelmät ovat 4. Seuraavaa XOR-totuustaulukkoa käyttämällä määritetään vastaava tulos. Tulos kaapataan muodossa C, tässä C = A ^ B.
Tässä totuustaulukossa otamme syötteen totuusarvojen muodossa, eli tosi ( T ) ja False ( F ). Tulos luodaan myös True-arvoina, eli T ja F.

Tässä yllä olevassa XOR Truth -taulukossa havaitaan, että kun operandien A ja B arvot ovat erilaiset, eli ( F, T ), ( T, F ), tulos tulee aina olemaan T. Ja kun Operandien A ja B arvot ovat samat, eli ( F, F ), ( T, T ), tuloksena tulee aina F.
Yllä olevista taulukoista huomaamme sen T (tosi) on merkitty ykkösellä ja F (false) on merkitty 0:lla.
Toimenpiteet minkä tahansa ongelman ratkaisemiseksi -
- Tehtävässä annetut operandit ovat aina desimaaliarvoina.
- Ensinnäkin meidän on muutettava operandien arvot arvoiksi binääri
- Kun olet muuntanut operandien arvot binääriluvuiksi, aseta molemmat operandit päällekkäin.
- Muista, että ennen kuin käytät niissä yksinomaista TAI (XOR) -toimintoa, tarkista ystävällisesti numeroiden määrä heissä.
- Jos numeroiden määrä ei täsmää, ylimääräiset nollat pienen operandin vasemmassa päässä tasapainottavat numeroiden määrän.
- Lopuksi sovelletaan yllä olevan totuustaulukon avulla XOR-operaatiota operandiin yksitellen ottaen bitti kerrallaan XOR-operaation soveltamista varten.
- Viimeinkin tulos tuotetaan tuotoksen muodossa.
- Tulos on binäärimuodossa. Muunna nyt binäärimuoto desimaalimuotoon ja merkitse tulosarvo muistiin.
Bitwise Exclusive OR (XOR) -operaation suorittaminen C++:ssa
Ymmärrämme yksityiskohtaisemmin XOR-operaation suorittamista C++:ssa esimerkkien avulla -
Esimerkki 1: Etsi kokonaislukuarvojen poissulkeva TAI; 10 ja 14. Selitä myös se ja kirjoita suorituskoodi C++:lla.
Ratkaisu: Tarkastellaan kahta muuttujaa ' a ' ja ' b ' tallentaaksemme vastaavat kaksi yllä olevassa kysymyksessä annettua operandia, eli 10 ja 14.
Tässä a = 10 ja b = 14.
Seuraamme alla olevia ohjeita saadaksemme selville annettujen kahden operandin yksinomaisen OR:n.
shreya ghoshal ensimmäinen aviomies
- Tiedämme, että 10 ja 14 ovat desimaalimuodossa, ja bittikohtaisen XOR-operaation soveltamiseksi se on muutettava binäärimuotoon.
- Binäärimuoto 'a', eli 10 on '1010' ja 'b':n binäärimuoto, eli 14 on '1110'.
- Tässä havaitaan, että a:ssa olevien binäärinumeroiden määrä on neljä ja b:ssä olevien binäärinumeroiden määrä on myös 4; siksi molemmissa muuttujissa olevien binäärinumeroiden määrä on sama ja jo tasapainotettu, meidän ei tarvitse lisätä enempää nollia sen tasapainottamiseksi.
- Laitetaan nyt 'b':ssä olevat binäärinumerot alas 'a':ssa oleviin binäärinumeroihin.
- Lopuksi XOR-operaation soveltaminen yksitellen vastaaviin bitteihin täsmää ja merkitse tulosteen muistiin.
- Viimeinkin generoitu tulos tulee olemaan binäärimuodossa, kuten yllä oleva kysymys on annettu desimaalimuodossa, joten tulos on muutettava desimaalimuotoon.
Selitys:
a = 10 ( desimaalimuodossa )
b = 14 ( desimaalimuodossa )
Nyt XOR b:lle meidän on muutettava a ja b binäärimuodossa -
a = 1010 (binäärimuodossa)
b = 1110 (binäärimuodossa)
Nyt sovelletaan XOR-operaatiota a:lle ja b -
a = 1010
b = 1110
----------------
a ^ b = 0100 ( Binäärimuodossa )
A ^ b:n tulos on 0100, joka on binäärimuodossa.
Muunnetaan nyt tulos desimaalimuotoon, joka on 4.
10^14 = 4
HUOMAA: Yllä olevaa XOR-totuustaulukkoa käyttämällä generoidaan vastaavien bittien lähtö.
Käytämme nyt bittikohtaista XOR-operaatiota 10:ssä ja 14:ssä C++-kielellä ja saamme tuloksen, eli 4.
dateformat.format
C++-koodi yllä olevaan esimerkkiin:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Lähtö

Esimerkki 2: Etsi kokonaislukuarvojen poissulkeva TAI; 3 ja 15. Selitä myös se ja kirjoita suorituskoodi C++:lla.
Ratkaisu: Tarkastellaan kahta muuttujaa ' a ' ja ' b ' tallentaaksemme vastaavat kaksi yllä olevassa kysymyksessä annettua operandia, eli 3 ja 15.
Tässä a = 3 ja b = 15.
Seuraamme alla olevia ohjeita saadaksemme selville annettujen kahden operandin yksinomaisen OR:n.
- Tiedämme, että 3 ja 15 ovat desimaalimuodossa, ja bittikohtaisen XOR-operaation soveltamiseksi se on muutettava binäärimuotoon.
- Binäärimuoto 'a', eli 3 on 'yksitoista' ja 'b':n binäärimuoto, eli 15 on '1111'.
- Tässä havaitaan, että a:ssa olevien binäärinumeroiden määrä on kaksi ja b:ssä olevien binäärinumeroiden määrä on neljä; siksi kummassakin muuttujassa olevien binäärinumeroiden määrä ei ole sama. Siksi epätasapainossa meidän on lisättävä enemmän nollia alemman binääriluvun vasemmalle puolelle, eli a, joka on ' yksitoista' , tasapainottamaan sitä.
- Tasapainotuksen jälkeen a:n arvo on '0011' , ja b on '1111'.
- Laitetaan nyt 'b':ssä olevat binäärinumerot alas 'a':n binäärinumeroihin.
- Lopuksi XOR-operaation soveltaminen yksitellen vastaaviin bitteihin täsmää ja merkitse tulosteen muistiin.
- Viimeinkin generoitu tulos tulee olemaan binäärimuodossa, kuten yllä oleva kysymys on annettu desimaalimuodossa, joten tulos on muutettava desimaalimuotoon.
Selitys:
a = 3 ( desimaalimuodossa )
b = 15 ( desimaalimuodossa )
Nyt XOR b:lle meidän on muutettava a ja b binäärimuodossa -
a = 0011 (binäärimuodossa)
b = 1111 (binäärimuodossa)
Nyt sovelletaan XOR-operaatiota a:lle ja b -
a = 0011
b = 1111
----------------
a ^ b = 1100 ( Binäärimuodossa )
A ^ b:n tulos on 1100, joka on binäärimuodossa.
Muunnetaan nyt tulos desimaalimuotoon, joka on 12.
3^15 = 12
HUOMAA: Yllä olevaa XOR-totuustaulukkoa käyttämällä generoidaan vastaavien bittien lähtö.
Käytämme nyt bittikohtaista XOR-operaatiota 3:lle ja 15:lle C++-kielellä ja saamme tuloksen, eli 12.
C++-koodi yllä olevaan esimerkkiin:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Lähtö

