A Laskuri on laite, joka tallentaa (ja joskus näyttää), kuinka monta kertaa tietty tapahtuma tai prosessi on tapahtunut, usein suhteessa kellosignaaliin. Laskuria käytetään digitaalisessa elektroniikassa laskentatarkoituksiin, ne voivat laskea tietyn piirissä tapahtuvan tapahtuman. Esimerkiksi UP-laskurissa laskuri kasvattaa kellon jokaisen nousevan reunan määrää. Laskuri ei vain laske, vaan voi seurata tiettyä järjestystä suunnittelumme perusteella kuten mikä tahansa satunnainen sekvenssi 0,1,3,2…. Ne voidaan suunnitella myös varvastossojen avulla. Niitä käytetään taajuudenjakajina, joissa tietyn pulssiaaltomuodon taajuus jaetaan. Laskurit ovat peräkkäisiä piirejä, jotka laskevat pulssien lukumäärän voivat olla joko binäärikoodissa tai BCD-muodossa. Laskurin tärkeimmät ominaisuudet ovat ajoitus, sekvensointi ja laskenta. Laskuri toimii kahdessa tilassa
Ylös laskuri
Alas laskuri
Laskuriluokitus
Laskurit on jaettu laajasti kahteen luokkaan
- Asynkroninen laskuri
- Synkroninen laskuri
1. Asynkroninen laskuri
Asynkronisessa laskurissa emme käytä yleiskelloa, vain ensimmäistä kiikkua ohjaa pääkello ja muun seuraavan kiikkun kellotuloa ohjaa aikaisempien kiikkujen lähtö. Voimme ymmärtää sen seuraavan kaavion avulla -
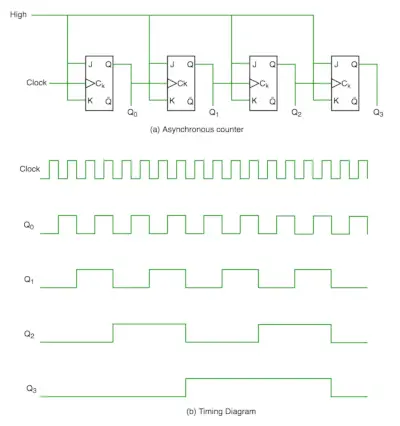
Ajoituskaaviosta on selvää, että Q0 muuttuu heti, kun kellopulssin nouseva reuna kohdataan, Q1 muuttuu, kun Q0:n nouseva reuna kohdataan (koska Q0 on kuin kellopulssi toiselle flip-flopille) ja niin edelleen. Tällä tavalla aaltoilua syntyy Q0, Q1, Q2, Q3 kautta, joten sitä kutsutaan myös RIPPLE-laskuri ja sarjalaskuri. Aaltoilulaskuri on kiikkujen peräkkäinen järjestely, jossa yhden kiikkun lähtö ohjaa seuraavan varvassyötön kellotuloa
2. Synkroninen laskuri
Toisin kuin asynkronisella laskurilla, synkronisella laskurilla on yksi globaali kello, joka ohjaa jokaista kiikkua niin, että lähtö muuttuu rinnakkain. Synkronisen laskurin yksi etu asynkroniseen laskuriin verrattuna on, että se voi toimia korkeammalla taajuudella kuin asynkroninen laskuri, koska sillä ei ole kumulatiivista viivettä, koska sama kello annetaan jokaiselle flip-flopille. Sitä kutsutaan myös rinnakkaislaskuriksi.
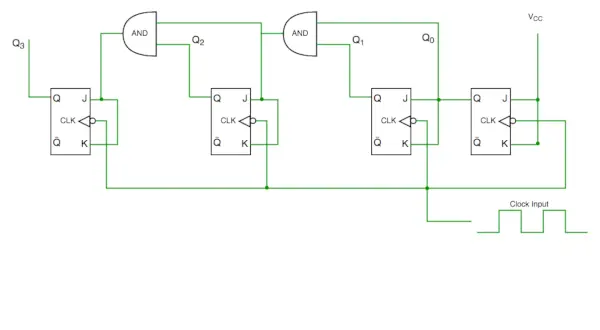
Synkroninen laskuripiiri
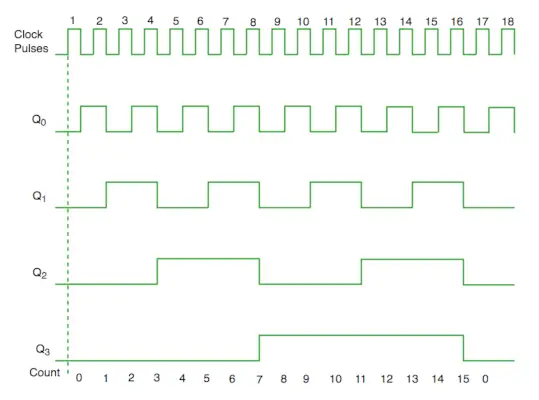
Ajoituskaavion synkroninen laskuri
Piirikaaviosta näemme, että Q0 bitti antaa vasteen kellon jokaiselle laskevalle reunalle, kun taas Q1 on riippuvainen Q0:sta, Q2 on riippuvainen Q1:stä ja Q0:sta, Q3 on riippuvainen Q2:sta, Q1:stä ja Q0:sta.
Vuosikymmenen laskuri
Vuosikymmenen laskuri laskee kymmenen erilaista tilaa ja nollaa sitten alkutilaansa. Yksinkertainen vuosikymmenlaskuri laskee välillä 0-9, mutta voimme myös tehdä vuosikymmenlaskurit, jotka voivat käydä läpi minkä tahansa kymmenen tilan välillä 0-15 (4-bittiselle laskurille).
| Kellon pulssi | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Totuustaulukko yksinkertaiseen vuosikymmenlaskuriin
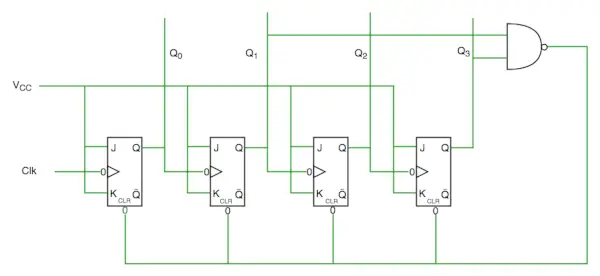
Vuosikymmenen laskurin piirikaavio
Näemme piirikaaviosta, että olemme käyttäneet nand-porttia Q3:lle ja Q1:lle ja syöttäneet tämän tyhjentämään tulolinjaa, koska luvun 10 binääriesitys on...
1010
Ja näemme, että Q3 ja Q1 ovat tässä 1, jos annamme näiden kahden bitin NAND-arvon tyhjennettäväksi syötteeksi, laskuri tyhjenee 10:ssä ja aloita jälleen alusta.
Tärkeä pointti : Laskurissa käytettyjen varvastossojen määrä on aina suurempi kuin ( Hirsi2n ) jossa n = laskurin tilojen lukumäärä.
Joitakin edellisten vuosien porttikysymyksiä laskurit
Q1. Harkitse 2-bittisen laskurin osittaista toteutusta käyttämällä T-kiikkuja, jotka seuraavat sekvenssiä 0-2-3-1-0, kuten alla on esitetty
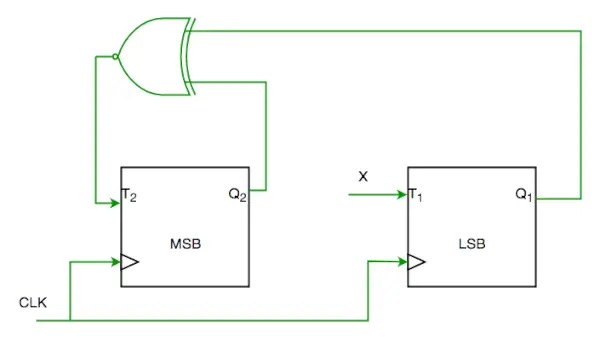
Piirin loppuun saattamiseksi tulon X tulee olla
(A) Q2?
(B) Q2 + Q1
(C) (Q1 ? Q2)'
(D) Q1? Q2 (GATE-CS-2004)
Ratkaisu:
Piiristä näemme
T1=XQ1’+X’Q1—-(1)
JA
T2=(Q2 ? Q1)'—-(2)
JA HALUATTU TULOS ON 00->10->11->01->00
NIN X PITÄÄ OLLA Q1Q2’+Q1’Q2 TYYTYVÄT 1 JA 2.
SIIN ON (D) OSA.
Q2. 4-bittisen binäärilaskurin ohjaussignaalitoiminnot on annettu alla (jossa X on välitä)
Laskuri on kytketty seuraavasti:
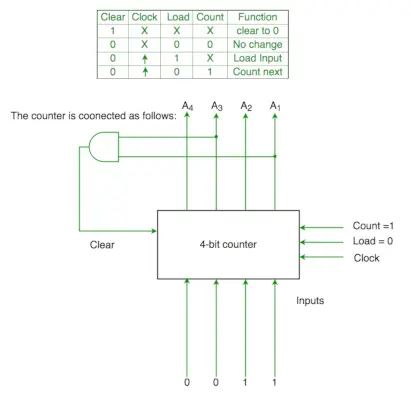
Oletetaan, että laskurin ja portin viiveet ovat merkityksettömiä. Jos laskuri alkaa nollasta, se käy läpi seuraavan sekvenssin:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (GATE-CS-2007)
Ratkaisu:
Aluksi A1 A2 A3 A4 = 0000
Clr = A1 ja A3
Joten kun A1 ja A3 ovat molemmat 1, se menee taas 0000:een
Tästä syystä 0000(alku.) -> 0001(A1 ja A3=0)->0010 (A1 ja A3=0) -> 0011(A1 ja A3=0) -> 0100 ( A1 ja A3 = 1 )[ selvä ehto täyttyy] ->0000(alkuperäinen) joten se menee läpi 0->1->2->3->4
Ans on (C) osa.
anaconda vs python käärme
Tietovisa digitaalisesta logiikasta
Anuj Bathamin kirjoittama artikkeli,
