Poista-toimintoa käytetään määritetyn solmun poistamiseen binäärihakupuusta. Meidän on kuitenkin poistettava solmu binäärihakupuusta siten, että binäärihakupuun ominaisuus ei riko. Solmun poistamiseen binäärihakupuusta on kolme tilannetta.
Poistettava solmu on lehtisolmu
Se on yksinkertaisin tapaus, tässä tapauksessa korvaa lehtisolmu NULL:lla ja vapauta varattu tila.
tyyppimuunnos ja valu javassa
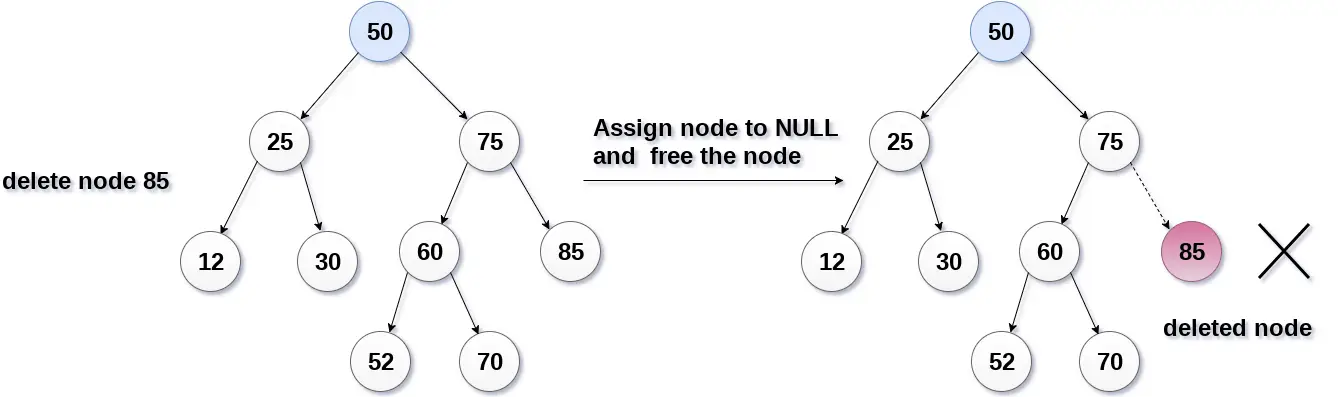
Seuraavassa kuvassa poistamme solmun 85, koska solmu on lehtisolmu, joten solmu korvataan NULL:lla ja varattu tila vapautuu.
Poistettavalla solmulla on vain yksi lapsi.
Tässä tapauksessa korvaa solmu sen lapsilla ja poista alisolmu, joka sisältää nyt poistettavan arvon. Korvaa se vain NULL:lla ja vapauta varattu tila.
Panda-sarjan ominaisuuksia
Seuraavassa kuvassa solmu 12 on poistettava. Sillä on vain yksi lapsi. Solmu korvataan sen lapsisolmulla ja korvattu solmu 12 (joka on nyt lehtisolmu) yksinkertaisesti poistetaan.

Poistettavalla solmulla on kaksi lasta.
Se on hieman monimutkainen tapaus verrattuna kahteen muuhun tapaukseen. Kuitenkin poistettava solmu korvataan sen järjestyksessä olevalla seuraajalla tai edeltäjällä rekursiivisesti, kunnes solmun arvo (poistettava) sijoitetaan puun lehteen. Korvaa toimenpiteen jälkeen solmu NULL:lla ja vapauta varattu tila.
Seuraavassa kuvassa on poistettava solmu 50, joka on puun juurisolmu. Alla oleva puun läpikulku järjestyksessä.
awt java
6, 25, 30, 50, 52, 60, 70, 75.
korvaa 50 sen seuraajalla 52. Nyt 50 siirretään puun lehteen, joka yksinkertaisesti poistetaan.

Algoritmi
Poista (TREE, ITEM)
Kirjoita 'tuote ei löydy puusta' ELSE IF ITEM DATA
Poista(PUU->VASEN, KOHDE)
MUUTA JOS TUOTE > PUU -> TIEDOT
Poista (PUU -> OIKEA, KOHDE)
MUUTA JOS PUU -> VASEN JA PUU -> OIKEA
SET TEMP = etsiSuurinsolmu(PUU -> VASEN)
SET TREE -> DATA = TEMP -> DATA
Poista (PUU -> VASEN, LÄMPÖ -> TIEDOT)
MUU
SET TEMP = PUU
JOS PUU -> VASEN = NOLLA JA PUU -> OIKEA = NOLLA
SET TREE = NULL
MUUTA JOS PUU -> VASEN != NULL
SET TREE = PUU -> VASEN
MUU
SET TREE = PUU -> OIKEA
[JOS LOPPU]
ILMAINEN LÄMPÖTILA
[JOS LOPPU]
Tehtävä:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 