Esimerkki 1:
Suunnittele NFA siirtymätaulukolle alla olevan mukaisesti:
| Nykyinen valtio | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | e |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Ratkaisu:
Siirtymäkaavio voidaan piirtää käyttämällä taulukon mukaista kartoitustoimintoa.
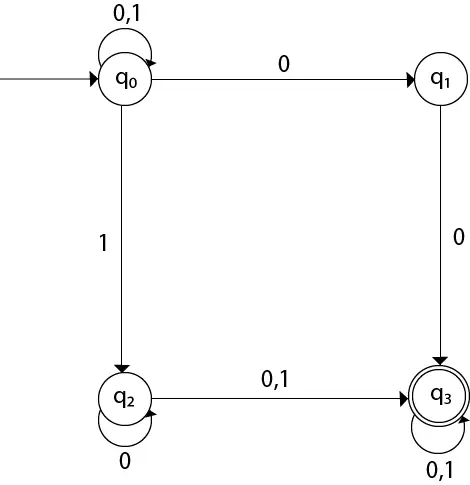
Tässä,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Esimerkki 2:
Suunnittele NFA, jossa ∑ = {0, 1} hyväksyy kaikki merkkijonot, jotka päättyvät 01:een.
char merkkijonoon
Ratkaisu:

Siksi NFA olisi:

Esimerkki 3:
Suunnittele NFA:lla ∑ = {0, 1}, jossa kaksinkertaista '1' seuraa kaksinkertainen '0'.
Ratkaisu:
nimisopimus java
FA kaksinkertaisella 1:llä on seuraava:

Sen jälkeen tulee välittömästi seurata kaksinkertainen 0.
Sitten,

Nyt ennen double 1:tä voi olla mikä tahansa merkkijono 0 ja 1. Vastaavasti double 0:n jälkeen voi olla mikä tahansa merkkijono 0 ja 1.
Tästä syystä NFA:sta tulee:
merkkijonomenetelmiä

Nyt kun otetaan huomioon merkkijono 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Esimerkki 4:
Suunnittele NFA, jossa kaikki merkkijonot sisältävät alimerkkijonon 1110.
Ratkaisu:
Kieli koostuu kaikista merkkijonoista, jotka sisältävät alimerkkijonon 1010. Osittainen siirtymäkaavio voi olla:

Nyt 1010 voisi olla osamerkkijono. Tästä syystä lisäämme syötteet 0:t ja 1:t, jotta kielen osamerkkijono 1010 voidaan säilyttää. Tästä syystä NFA:sta tulee:
system.out.println

Siirtymätaulukko yllä olevalle siirtymäkaaviolle voidaan antaa alla:
| Nykyinen valtio | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Harkitse merkkijonoa 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Juuttui! Koska syötesymbolille 0 ei ole polkua q2:sta. Voimme käsitellä merkkijonoa 111010 toisella tavalla.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Koska tila q5 on hyväksymistila. Saamme täydellisen skannatun ja pääsimme lopulliseen tilaan.
Esimerkki 5:
Suunnittele NFA, jossa ∑ = {0, 1} hyväksyy kaikki merkkijonot, joissa kolmas symboli oikeasta päästä on aina 0.
str to int
Ratkaisu:

Siten saamme kolmannen symbolin oikeasta päästä aina '0':na. NFA voi olla:

Yllä oleva kuva on NFA, koska tilassa q0 syötteellä 0 voimme siirtyä joko tilaan q0 tai q1.
