logo

TechCodeview

Floyd Warshall -algoritmi

The Floyd-Warshall-algoritmi , joka on nimetty sen tekijöiden mukaan Robert Floyd ja Stephen Warshall , on tietojenkäsittelytieteen ja graafiteorian perusalgoritmi. Sitä käytetään lyhimpien polkujen löytämiseen painotetun graafin kaikkien solmuparien välillä. Tämä algoritmi on erittäin tehokas ja pystyy käsittelemään kaavioita molemmilla positiivinen ja n tasapainot , joten se on monipuolinen työkalu useiden verkko- ja yhteysongelmien ratkaisemiseen.

Sisällysluettelo

Floyd-Warshall-Algoritmi-banneri



Floyd Warshall -algoritmi:

The Floyd Warshall -algoritmi on kaikkien parien lyhimmän polun algoritmi toisin kuin Dijkstra ja Bellman Ford jotka ovat yhden lähteen lyhimmän polun algoritmeja. Tämä algoritmi toimii molemmille ohjattu ja suuntaamaton painotettu kaavioita. Mutta se ei toimi kaavioissa, joissa on negatiivinen sykli (jossa syklin reunojen summa on negatiivinen). Se seuraa Dynaaminen ohjelmointi lähestymistapa tarkistaa kaikki mahdolliset polut, jotka kulkevat jokaisen mahdollisen solmun kautta, jotta voidaan laskea lyhin etäisyys jokaisen solmuparin välillä.

java valinta lajitella

Idea Floyd Warshall -algoritmin takana:

Oletetaan, että meillä on kaavio G[][] kanssa SISÄÄN kärjet alkaen 1 to N . Nyt meidän on arvioitava a shortestPathMatrix[][] missä s hortestPathMatrix[i][j] edustaa lyhintä polkua pisteiden välillä i ja j .

Ilmeisesti lyhin reitti välillä i to j tulee joitakin k välisolmujen määrä. Floyd warshall -algoritmin ideana on käsitellä jokaista huippupistettä 1 to N välisolmuna yksitellen.

Seuraava kuva näyttää yllä olevan optimaalisen alirakenteen ominaisuuden floyd warshall -algoritmissa:

Floyd Warshall -algoritmi:

  • Alusta ratkaisumatriisi samalla tavalla kuin syötekaaviomatriisi ensimmäisenä vaiheena.
  • Päivitä sitten ratkaisumatriisi pitämällä kaikki kärjet välipisteinä.
  • Ajatuksena on valita kaikki kärjet yksitellen ja päivittää kaikki lyhyimmät polut, jotka sisältävät poimitun kärjen välipisteenä lyhyimmässä polussa.
  • Kun valitsemme huippunumeron k välipisteenä olemme jo tarkastelleet kärkipisteitä 0, 1, 2, .. k-1} välipisteinä.
  • Jokaiselle parille (i, j) lähde- ja kohdepisteiden kohdalla on kaksi mahdollista tapausta.
    • k ei ole välipiste lyhimmän polun päässä i to j . Pidämme arvon dist[i][j] niin kuin se on.
    • k on välipiste lyhimmän polun päässä i to j . Päivitämme arvon dist[i][j] kuten dist[i][k] + dist[k][j], jos dist[i][j]> dist[i][k] + dist[k][j]

Floyd Warshall -algoritmin pseudokoodi:>

Kun k = 0 - n - 1
Jos i = 0 - n - 1
Jos j = 0 - n - 1
Etäisyys[i, j] = min(etäisyys[i, j], etäisyys[i, k] + etäisyys[k, j])

missä i = lähdesolmu, j = kohdesolmu, k = välisolmu

Kuva Floyd Warshall -algoritmista:

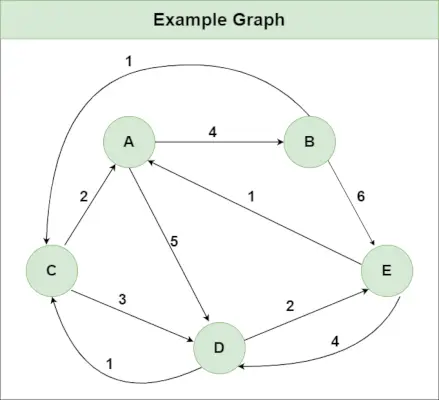
Oletetaan, että meillä on kuvan mukainen kaavio:

apple emojit Androidissa
dryRun1drawio

Vaihe 1 : Alusta Etäisyys[][]-matriisi käyttämällä syötekaaviota siten, että Etäisyys[i][j]= reunan paino i to j , myös Etäisyys[i][j] = Ääretön, jos ei ole reunaa alkaen i to j.

step1drawio

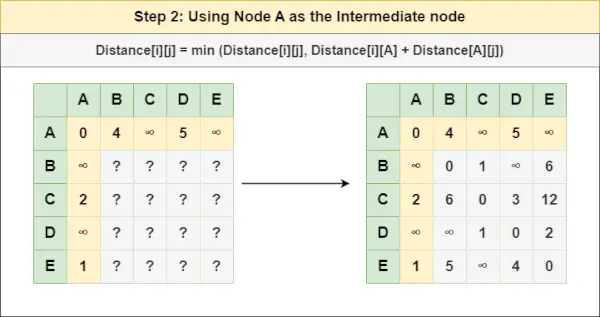
Vaihe 2 : Käsittele solmua A välisolmuna ja laske Etäisyys[][] jokaiselle {i,j} solmuparille käyttämällä kaavaa:

= Etäisyys[i][j] = pienin (etäisyys[i][j], (etäisyys i:stä A ) + (Etäisyys A kohtaan j))
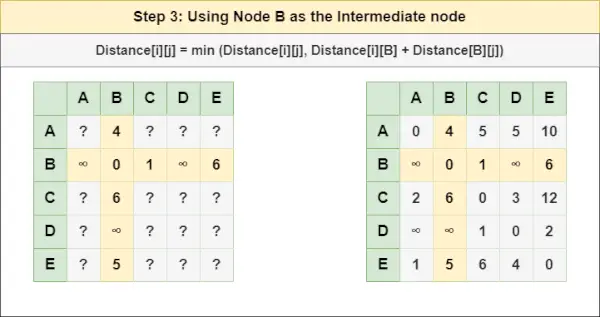
= Etäisyys[i][j] = pienin (etäisyys[i][j], etäisyys[i][ A ] + etäisyys[ A ][j])

step2drawio

Vaihe 3 : Käsittele solmua B välisolmuna ja laske etäisyys[][] jokaiselle {i,j} solmuparille käyttämällä kaavaa:

= Etäisyys[i][j] = pienin (etäisyys[i][j], (etäisyys i:stä B ) + (Etäisyys B kohtaan j))
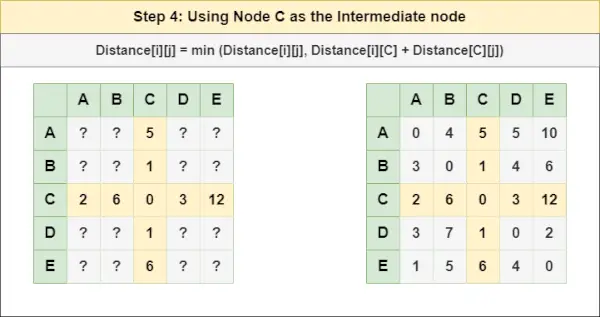
= Etäisyys[i][j] = pienin (etäisyys[i][j], etäisyys[i][ B ] + Etäisyys[ B ][j])

step3drawio

Vaihe 4 : Käsittele solmua C välisolmuna ja laske etäisyys[][] jokaiselle {i,j} solmuparille käyttämällä kaavaa:

= Etäisyys[i][j] = pienin (etäisyys[i][j], (etäisyys i:stä C ) + (Etäisyys C kohtaan j))
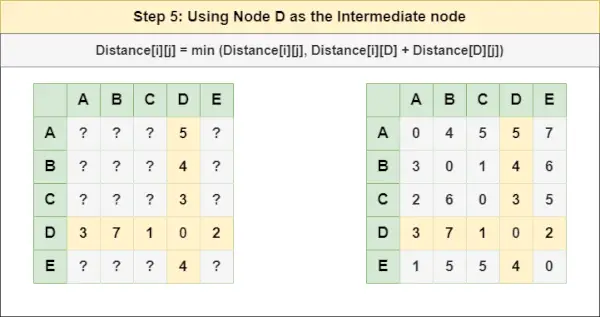
= Etäisyys[i][j] = pienin (etäisyys[i][j], etäisyys[i][ C ] + etäisyys[ C ][j])

step4dravio

Vaihe 5 : Käsittele solmua D välisolmuna ja laske etäisyys[][] jokaiselle {i,j} solmuparille käyttämällä kaavaa:

lista taulukkona

= Etäisyys[i][j] = pienin (etäisyys[i][j], (etäisyys i:stä D ) + (Etäisyys D kohtaan j))
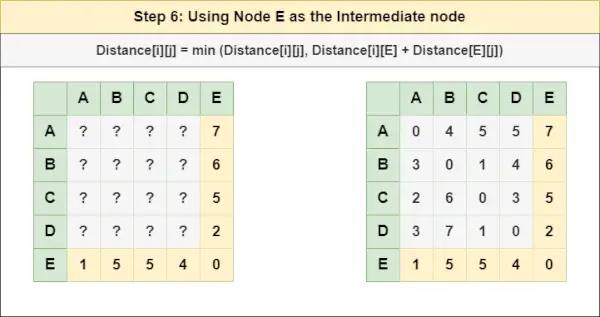
= Etäisyys[i][j] = pienin (etäisyys[i][j], etäisyys[i][ D ] + Etäisyys[ D ][j])

step5drawio

Vaihe 6 : Käsittele solmua JA välisolmuna ja laske etäisyys[][] jokaiselle {i,j} solmuparille käyttämällä kaavaa:

= Etäisyys[i][j] = pienin (etäisyys[i][j], (etäisyys i:stä JA ) + (Etäisyys JA kohtaan j))
= Etäisyys[i][j] = pienin (etäisyys[i][j], etäisyys[i][ JA ] + Etäisyys[ JA ][j])

step6drawio

Vaihe 7 : Koska kaikkia solmuja on käsitelty välisolmuina, voimme nyt palauttaa päivitetyn Distance[][]-matriisin vastausmatriisiksi.

step7drawio
Suositeltu käytäntö Kokeile!

Alla on yllä olevan lähestymistavan toteutus:

C++ 
// C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Ennen iteroinnin aloittamista meillä on lyhyimmät etäisyydet kaikkien kärkiparien välillä siten, että lyhyimmät etäisyydet pitävät vain joukon {0, 1, 2, .. k-1} kärjet välipisteinä.  ----> Iteroinnin päätyttyä kärki nro. k lisätään välipisteiden joukkoon ja joukosta tulee {0, 1, 2, .. k} */ kun (k = 0; k)< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Tulosta lyhimmän matkan matriisi printSolution(dist); } /* Aputoiminto ratkaisun tulostamiseen */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int kaavio[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, { INF, INF, INF, 0}};  // Funktion kutsu floydWarshall(graph);  paluu 0; } // Tämän koodin on toimittanut Mythri J L>>C(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int kaavio[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, { INF, INF, INF, 0}};  // Funktion kutsu floydWarshall(graph);  paluu 0; }>
Java 
// Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Ennen iteroinnin aloittamista meillä on lyhyimmät etäisyydet kaikkien kärkiparien välillä siten, että lyhyimmät etäisyydet pitävät vain joukon {0, 1, 2, .. k-1} kärjet välipisteinä.  ----> Iteroinnin päätyttyä kärki nro. k lisätään välipisteiden joukkoon ja joukosta tulee {0, 1, 2, .. k} */ kun (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int kaavio[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Funktiokutsu a.floydWarshall(graph);  } } // Tekijä: Aakash Hasija>
Python 3 
# Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Ennen iteroinnin alkua meillä on lyhyimmät etäisyydet kaikkien kärkiparien välillä siten, että lyhyimmät etäisyydet pitävät vain joukon {0, 1, 2, .. k-1} kärjet välipisteinä.  ----> Iteroinnin päätyttyä kärki nro. k lisätään välipisteiden joukkoon ja joukosta tulee 0, 1, 2, .. k} ''' k:lle alueella(V): # valitse kaikki kärjet lähteeksi yksitellen i:lle alue(V): # Valitse kaikki kärjet kohteeksi # yllä valitulle lähteelle j:lle alueella (V): # Jos kärki k on lyhimmällä polulla # i - j, päivitä dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Aputoiminto tulostaa ratkaisun def printSolution (dist): print('Seuraava matriisi näyttää lyhyimmat etäisyydet jokaisen pisteparin välillä') i:lle alueella(V): j:lle alueella(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Ohjaimen koodi if __nimi__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' kaavio = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Funktiokutsu floydWarshall(graph) # Tämän koodin tarjoaa Mythri J L>
C# 
// C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Ennen iteraation alkua meillä on lyhyimmät etäisyydet kaikkien kärkiparien välillä siten, että lyhyimmät etäisyydet pitävät vain joukon {0, 1, 2, .. k-1} kärjet välipisteinä.  ---> Iteraation päätyttyä kärki nro. k lisätään välipisteiden joukkoon ja joukosta tulee {0, 1, 2, .. k} */ kun (k = 0; k)< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] kaavio = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Funktiokutsu a.floydWarshall(graph);  } } // Tämän artikkelin on kirjoittanut // Abdul Mateen Mohammed>>Javascript(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var kaavio = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = new AllPairShortestPath();  // Tulosta ratkaisu a.floydWarshall(graph);    // Tämän koodin tarjoaa rdtaank.>>PHP(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $kaavio = array(taulukko(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), array($INF, $INF, $INF, 0)); // Funktion kutsu floydWarshall($graph, $V, $INF); // Tämän koodin tarjoaa Ryuga ?>>>
Lähtö 
The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Floyd Warshall -algoritmin monimutkaisuusanalyysi:

  • Aika monimutkaisuus: O(V3), jossa V on graafin kärkien lukumäärä ja suoritamme kolme sisäkkäistä silmukkaa, joiden koko on V
  • Aputila: O(V2), luodaksesi 2D-matriisin lyhimmän etäisyyden tallentamiseksi kullekin solmuparille.

Huomautus : Yllä oleva ohjelma tulostaa vain lyhimmät etäisyydet. Ratkaisua voidaan muokata lyhimpien polkujen tulostamiseksi myös tallentamalla edeltäjätiedot erilliseen 2D-matriisiin.

tallennettu ohjelman ohjaus

Miksi Floyd-Warshall-algoritmi on parempi tiheille kaavioille eikä harvoille kuvaajille?

Tiheä graafi : Graafi, jossa reunojen määrä on huomattavasti suurempi kuin kärkien lukumäärä.
Harva kaavio : Kaavio, jossa reunojen määrä on hyvin pieni.

Ei ole väliä kuinka monta reunaa kaaviossa on Floyd Warshall -algoritmi toimii O(V3) kertaa, joten se sopii parhaiten Tiheät kaaviot . Harvaiden kaavioiden tapauksessa Johnsonin algoritmi on sopivampi.

  • Kuinka havaita negatiivinen sykli kaaviossa Floyd Warshall -algoritmin avulla?
  • Miten Floyd-warshall-algoritmi eroaa Dijkstran algoritmista?
  • Miten Floyd-warshall-algoritmi eroaa Bellman-Ford-algoritmista?

Floyd-Warshall-algoritmin todelliset sovellukset:

  • Tietokoneverkoissa algoritmin avulla voidaan löytää lyhin polku verkon kaikkien solmuparien välillä. Tätä kutsutaan nimellä verkon reititys .
  • Lentoyhteydet Ilmailualalla löytää lyhin reitti lentokenttien välillä.
  • GIS ( Paikkatietojärjestelmät ) sovelluksissa usein analysoidaan paikkatietoja, kuten tieverkkoja, lyhimpien reittien löytämiseksi paikkojen välillä.
  • Kleenen algoritmi joka on yleistys sanasta floyd warshall, voidaan käyttää säännöllisen lausekkeen löytämiseen säännölliselle kielelle.