- Mäkikiipeilyalgoritmi on paikallinen hakualgoritmi, joka liikkuu jatkuvasti nousun/arvon suuntaan löytääkseen vuoren huipun tai parhaan ratkaisun ongelmaan. Se päättyy, kun se saavuttaa huippuarvon, jossa millään naapurilla ei ole korkeampaa arvoa.
- Mäkikiipeilyalgoritmi on tekniikka, jota käytetään matemaattisten ongelmien optimointiin. Yksi laajalti käsitellyistä esimerkeistä mäkikiipeilyalgoritmista on Travelling-salesman Problem, jossa meidän täytyy minimoida myyjän kulkema matka.
- Sitä kutsutaan myös ahneeksi paikallishakuksi, koska se katsoo vain hyvään välittömään naapurivaltioonsa eikä sen pidemmälle.
- Mäkikiipeilyalgoritmin solmussa on kaksi komponenttia, jotka ovat tila ja arvo.
- Mäkikiipeilyä käytetään enimmäkseen, kun hyvä heuristiikka on saatavilla.
- Tässä algoritmissa meidän ei tarvitse ylläpitää ja käsitellä hakupuuta tai kaaviota, koska se säilyttää vain yhden nykyisen tilan.
Mäkikiipeilyn ominaisuudet:
Seuraavassa on joitain mäkikiipeilyalgoritmin pääominaisuuksia:
Tila-avaruuskaavio mäkikiipeilyä varten:
Tila-avaruusmaisema on graafinen esitys mäkikiipeilyalgoritmista, joka näyttää kaavion algoritmin eri tilojen ja tavoitefunktion/kustannusten välillä.
Y-akselilla on otettu funktio, joka voi olla tavoitefunktio tai kustannusfunktio, ja tila-avaruus x-akselilla. Jos Y-akselin funktio on kustannus, haun tavoitteena on löytää globaali minimi ja paikallinen minimi. Jos Y-akselin funktio on Objektiivifunktio, niin haun tavoitteena on löytää globaali maksimi ja paikallinen maksimi.
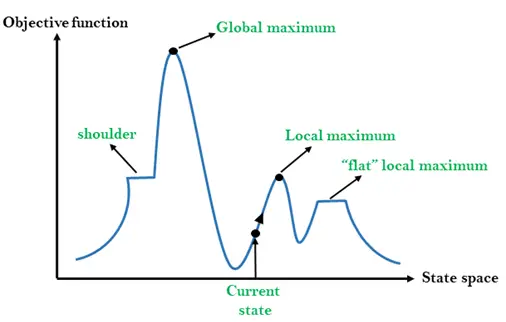
Eri alueet valtion avaruusmaisemassa:
Paikallinen enimmäismäärä: Paikallinen maksimi on tila, joka on parempi kuin sen naapurivaltiot, mutta on myös toinen tila, joka on sitä korkeampi.
Maailmanlaajuinen enimmäismäärä: Globaali maksimi on tila-avaruusmaiseman paras mahdollinen tila. Sillä on suurin tavoitefunktion arvo.
Nykyinen tila: Se on maisemakaavion tila, jossa agentti on tällä hetkellä läsnä.
Tasainen paikallinen maksimi: Se on tasainen tila maisemassa, jossa kaikilla nykyisten valtioiden naapurivaltioilla on sama arvo.
Olkapää: Se on tasangon alue, jolla on ylämäkeen reuna.
Mäkikiipeilyalgoritmien tyypit:
- Yksinkertainen mäkikiipeily:
- Jyrkin nousu mäkikiipeily:
- Stokastinen mäkikiipeily:
1. Yksinkertainen mäkikiipeily:
Yksinkertainen mäkikiipeily on yksinkertaisin tapa toteuttaa mäkikiipeilyalgoritmi. Se arvioi vain naapurisolmun tilan kerrallaan ja valitsee ensimmäisen, joka optimoi nykyiset kustannukset ja asettaa sen nykyiseksi tilaksi . Se tarkistaa vain, että se on yksi seuraajatila, ja jos se löytää paremman kuin nykyinen tila, siirry muuhun samaan tilaan. Tällä algoritmilla on seuraavat ominaisuudet:
- Vähemmän aikaa vievää
- Vähemmän optimaalinen ratkaisu ja ratkaisua ei taata
Algoritmi yksinkertaiselle mäkikiipeilylle:
- Jos se on tavoitetila, palauta menestys ja lopeta.
- Muussa tapauksessa, jos se on parempi kuin nykyinen tila, määritä uusi tila nykyiseksi tilaksi.
- Muussa tapauksessa, jos ei parempi kuin nykyinen tila, palaa vaiheeseen 2.
2. Jyrkimmän nousun mäkikiipeily:
Jyrkimmän nousun algoritmi on muunnelma yksinkertaisesta mäkikiipeilyalgoritmista. Tämä algoritmi tutkii kaikki nykyisen tilan naapurisolmut ja valitsee yhden naapurisolmun, joka on lähinnä tavoitetilaa. Tämä algoritmi kuluttaa enemmän aikaa, kun se etsii useita naapureita
Jyrkimmän nousun mäkikiipeilyn algoritmi:
- Olkoon SUCC sellainen tila, että mikä tahansa nykyisen tilan seuraaja on sitä parempi.
- Jokaiselle operaattorille, joka koskee nykyistä tilaa:
- Käytä uutta operaattoria ja luo uusi tila.
- Arvioi uusi tila.
- Jos se on tavoitetila, palauta se ja lopeta, muuten vertaa sitä SUCC:hen.
- Jos se on parempi kuin SUCC, aseta uudeksi tilaksi SUCC.
- Jos SUCC on parempi kuin nykyinen tila, aseta nykyinen tila SUCC:ksi.
3. Stokastinen mäkikiipeily:
Stokastinen mäkikiipeily ei tutki kaikkia naapuriaan ennen muuttoa. Pikemminkin tämä hakualgoritmi valitsee yhden naapurisolmun satunnaisesti ja päättää, valitaanko sen nykyiseksi tilaksi vai tutkitaanko toista tilaa.
Ongelmia mäkikiipeilyalgoritmissa:
1. Paikallinen enimmäismäärä: Paikallinen maksimi on maiseman huipputila, joka on parempi kuin jokainen naapuritila, mutta on myös toinen tila, joka on korkeampi kuin paikallinen maksimi.
Ratkaisu: Backtracking-tekniikka voi olla ratkaisu paikallisen maksimiin tila-avaruusmaisemassa. Luo luettelo lupaavasta polusta, jotta algoritmi voi palata hakutilaan ja tutkia myös muita polkuja.
java-merkkijono jsoniin

2. Tasango: Tasanne on hakuavaruuden tasainen alue, jossa kaikki nykyisen tilan naapuritilat sisältävät saman arvon, koska tämä algoritmi ei löydä parasta liikesuuntaa. Mäkikiipeilyhaku voi kadota tasangon alueella.
Ratkaisu: Ratkaisu tasangolle on ottaa suuria tai hyvin pieniä askelia etsiessään, ratkaista ongelma. Valitse satunnaisesti tila, joka on kaukana nykyisestä tilasta, jotta on mahdollista, että algoritmi löytää ei-tasangon alueen.

3. Harjanteet: Harju on paikallisen maksimin erityinen muoto. Sen alue on korkeampi kuin ympäröivät alueet, mutta sillä on kaltevuus, eikä sinne pääse yhdellä liikkeellä.
Ratkaisu: Tätä ongelmaa voidaan parantaa käyttämällä kaksisuuntaista hakua tai liikkumalla eri suuntiin.

Simuloitu hehkutus:
Mäkikiipeilyalgoritmi, joka ei koskaan siirry alempaan arvoon, on taatusti epätäydellinen, koska se voi juuttua paikalliseen maksimiin. Ja jos algoritmi käyttää satunnaista kävelyä siirtämällä seuraajaa, se saattaa valmistua, mutta ei tehokasta. Simuloitu hehkutus on algoritmi, joka tuottaa sekä tehokkuutta että täydellisyyttä.
Mekaanisesti sanottuna Hehkutus on prosessi, jossa metalli tai lasi kovetetaan korkeaan lämpötilaan ja jäähdytetään sitten vähitellen, jolloin metalli saavuttaa matalan energian kiteisen tilan. Samaa prosessia käytetään simuloidussa hehkutuksessa, jossa algoritmi valitsee satunnaisen liikkeen parhaan liikkeen valitsemisen sijaan. Jos satunnainen liike parantaa tilaa, se seuraa samaa polkua. Muussa tapauksessa algoritmi seuraa polkua, jonka todennäköisyys on pienempi kuin 1, tai se liikkuu alamäkeen ja valitsee toisen polun.
