Perinteisten binäärihakupuiden rajoitukset voivat olla turhauttavia. Tapaa B-Tree, monilahjakas tietorakenne, joka pystyy käsittelemään valtavia tietomääriä helposti. Kun on kyse suurten tietomäärien tallentamisesta ja etsimisestä, perinteiset binäärihakupuut voivat tulla epäkäytännöllisiksi huonon suorituskyvyn ja suuren muistin käytön vuoksi. B-Trees, joka tunnetaan myös nimellä B-Tree tai Balanced Tree, ovat eräänlainen itsetasapainottava puu, joka on erityisesti suunniteltu voittamaan nämä rajoitukset.
Perinteisistä binäärihakupuista poiketen B-Puille on ominaista suuri määrä avaimia, jotka ne voivat tallentaa yhteen solmuun, minkä vuoksi niitä kutsutaan myös suuriksi avainpuiksi. Jokainen solmu B-puussa voi sisältää useita avaimia, mikä mahdollistaa puun suuremman haarautumiskertoimen ja siten matalamman korkeuden. Tämä matala korkeus vähentää levyn I/O:ta, mikä johtaa nopeampiin haku- ja lisäystoimintoihin. B-Trees soveltuu erityisen hyvin tallennusjärjestelmiin, joissa on hidas ja suuri datayhteys, kuten kiintolevyt, flash-muisti ja CD-ROM-levyt.
B-Trees ylläpitää tasapainoa varmistamalla, että jokaisella solmulla on vähimmäismäärä avaimia, joten puu on aina tasapainossa. Tämä tasapaino takaa, että toimintojen, kuten lisäyksen, poistamisen ja haun, aika monimutkaisuus on aina O(log n), riippumatta puun alkuperäisestä muodosta.
B-puun aika monimutkaisuus:
| Herra Ei. | Algoritmi | Aika monimutkaisuus |
|---|---|---|
| 1. | Hae | O(log n) |
| 2. | Lisää | O(log n) |
| 3. | Poistaa | O(log n) |
Huomautus: n on B-puun elementtien kokonaismäärä
resurssien allokaatiokaavio
B-Treen ominaisuudet:
- Kaikki lehdet ovat samalla tasolla.
- B-puu määritellään termillä vähimmäisaste ' t ‘. Arvo ' t ' riippuu levylohkon koosta.
- Jokaisen solmun juurta lukuun ottamatta tulee sisältää vähintään t-1 avaimet. Juuri voi sisältää vähintään 1 avain.
- Kaikki solmut (myös juuri) voivat sisältää enintään ( 2*t – 1 ) avaimet.
- Solmun lapsien lukumäärä on yhtä suuri kuin siinä olevien avainten määrä plus 1 .
- Kaikki solmun avaimet lajitellaan kasvavassa järjestyksessä. Lapsi kahden avaimen välissä k1 ja k2 sisältää kaikki avaimet alueella alkaen k1 ja k2 .
- B-Tree kasvaa ja kutistuu juuresta, mikä on toisin kuin Binary Search Tree. Binäärihakupuut kasvavat alaspäin ja myös kutistuvat alaspäin.
- Kuten muutkin tasapainotetut binaarihakupuut, etsimisen, lisäämisen ja poistamisen aika monimutkaisuus on O(log n).
- Solmun lisääminen B-puuhun tapahtuu vain lehtisolmussa.
Seuraavassa on esimerkki B-puusta, jonka tilavuus on vähintään 5
Huomautus: että käytännön B-Treesissä minimitilauksen arvo on paljon suurempi kuin 5.

Yllä olevasta kaaviosta voidaan nähdä, että kaikki lehtien solmut ovat samalla tasolla ja kaikilla ei-lehdillä ei ole tyhjää alipuuta ja avaimia on yksi vähemmän kuin heidän lastensa lukumäärä.
Mielenkiintoisia faktoja B-puista:
- B-puun vähimmäiskorkeus, joka voi olla olemassa n määrällä solmuja ja m on solmun lapsien enimmäismäärä, on:
- B-puun enimmäiskorkeus, joka voi olla olemassa n määrällä solmuja ja t on pienin määrä lapsia, joka ei-juurisolmulla voi olla:
ja
Läpikulku B-puussa:
Traversal on myös samanlainen kuin Inorder traversal of Binary Tree. Aloitamme vasemmanpuoleisesta lapsesta, tulostamme rekursiivisesti vasemmanpuoleisen lapsen ja toistamme sitten saman prosessin muille lapsille ja avaimille. Tulosta lopuksi rekursiivisesti oikeanpuoleisin lapsi.
Hakutoiminto B-puussa:
Haku on samanlainen kuin binaarihakupuun haku. Olkoon etsittävä avain k.
- Aloita juuresta ja kulje rekursiivisesti alaspäin.
- Jokaista vierailtua ei-lehtisolmua kohden,
- Jos solmulla on avain, palautamme solmun.
- Muussa tapauksessa palaamme solmun sopivaan aliryhmään (lapsi, joka on juuri ennen ensimmäistä suurempaa avainta).
- Jos saavutamme lehtisolmun, emmekä löydä k:tä lehtisolmusta, palauta NULL.
B-puun etsiminen on samanlaista kuin binääripuun etsiminen. Algoritmi on samanlainen ja toimii rekursion kanssa. Jokaisella tasolla haku optimoidaan ikään kuin avainarvo ei ole ylätason alueella, niin avain on toisessa haarassa. Koska nämä arvot rajoittavat hakua, niitä kutsutaan myös raja-arvoiksi tai erotusarvoiksi. Jos saavutamme lehtisolmun, emmekä löydä haluttua avainta, se näyttää NULL.
Algoritmi elementin etsimiseksi B-puusta:-
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->näppäin[i]) {> >i++;> >}> >if> (i n && k == x->avain[i]) {> >return> x;> >}> >if> (x->lehti) {> >return> nullptr;> >}> >return> BtreeSearch(x->lapsi[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python 3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.avain[i]: i += 1, jos i ja k == x.avain[i]: palauta x, jos x.leaf: palauta Ei mitään palauttaa BtreeSearch(x.lapsi[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Esimerkkejä:
löytää estettyjä numeroita Androidista
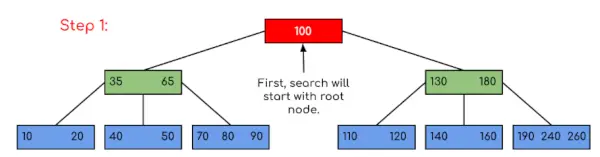
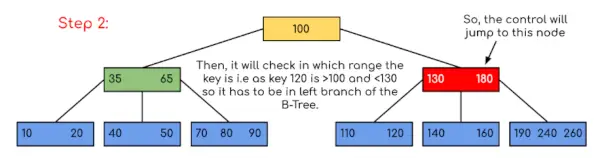
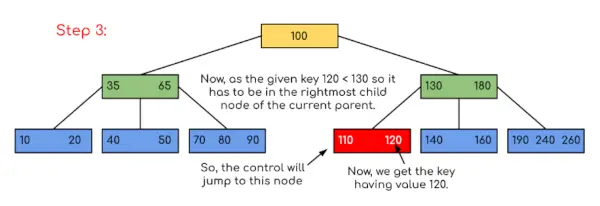
Syöte: Hae 120 annetusta B-puusta.
Ratkaisu:
kuinka monta missio mahdotonta elokuvaa on olemassa
Tässä esimerkissä voimme nähdä, että hakuamme väheni vain rajoittamalla mahdollisuuksia, joissa arvon sisältävä avain voisi olla läsnä. Vastaavasti, jos yllä olevassa esimerkissä meidän on etsittävä 180, ohjaus pysähtyy vaiheeseen 2, koska ohjelma havaitsee, että avain 180 on läsnä nykyisessä solmussa. Ja samalla tavalla, jos se etsii 90, niin 90 <100, joten se siirtyy automaattisesti vasemmalle alipuulle, ja siksi ohjausvirta kulkee samalla tavalla kuin yllä olevassa esimerkissä.
Alla on yllä olevan lähestymistavan toteutus:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->haku(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->traverse(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->traverse(); } // Toiminto avaimen k etsimiseksi alipuusta, jonka juuret ovat tällä solmulla BTreeNode* BTreeNode::search(int k) { // Etsi ensimmäinen avain, joka on suurempi tai yhtä suuri kuin k int i = 0; while (i näppäimet[i]) i++; // Jos löydetty avain on yhtä suuri kuin k, palauta tämä solmu if (avaimet[i] == k) palauttaa tämän; // Jos avainta ei löydy täältä ja tämä on lehtisolmu if (leaf == true) return NULL; // Siirry oikeaan alipalautukseen C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python 3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 ja k[0] 0]: i -= 1 i += 1, jos len(x.lapsi[i].avaimet) == (2 * itse.t) - 1: itse.split_child(x, i) jos k[0]> x.avaimet[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Jaa lapsi def split_child(itse, x, i): t = itse .t y = x.lapsi[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.avaimet = y.avaimet[t: (2 * t) - 1] y.avaimet = y.avaimet[0: t - 1] jos ei y.leaf: z.lapsi = y.lapsi[t: 2 * t] y. lapsi = y.lapsi[0: t - 1] # Tulosta puu def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') for i in x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: for i in x.child: self.print_tree(i, l) # Hakuavain puusta def search_key(self, k, x=Ei mitään): jos x ei ole Ei mitään: i = 0, kun taas i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Huomautus: Yllä oleva koodi ei sisällä ohjainohjelmaa. Kerromme koko ohjelman seuraavassa postauksessamme B-puun lisäys .
B-puun määrittämiseen on kaksi käytäntöä, yksi on määritellä minimiasteen mukaan, toinen on määrittää järjestyksen mukaan. Olemme noudattaneet vähimmäistutkintosopimusta ja noudatamme samaa tulevissa B-Treen postauksissa. Myös yllä olevassa ohjelmassa käytetyt muuttujien nimet säilytetään ennallaan
java-iteraattori kartalle
B-puiden sovellukset:
- Sitä käytetään suurissa tietokannoissa päästämään käsiksi levylle tallennettuihin tietoihin
- Tietojen etsiminen tietojoukosta voidaan suorittaa huomattavasti lyhyemmässä ajassa käyttämällä B-puuta
- Indeksointiominaisuuden avulla voidaan saavuttaa monitasoinen indeksointi.
- Suurin osa palvelimista käyttää myös B-puun lähestymistapaa.
- B-puita käytetään CAD-järjestelmissä geometrisen tiedon järjestämiseen ja etsimiseen.
- B-puita käytetään myös muilla aloilla, kuten luonnollisen kielen käsittelyssä, tietokoneverkoissa ja kryptografiassa.
B-puiden edut:
- B-puilla on taattu aikamonimutkaisuus O(log n) perustoimintoihin, kuten lisäämiseen, poistamiseen ja etsimiseen, mikä tekee niistä sopivia suurille tietojoukoille ja reaaliaikaisille sovelluksille.
- B-puut tasapainottavat itsensä.
- Korkea samanaikaisuus ja suuri suorituskyky.
- Tehokas tallennustilan käyttö.
B-puiden haitat:
- B-puut perustuvat levypohjaisiin tietorakenteisiin ja niillä voi olla paljon levyn käyttöä.
- Ei paras kaikkiin tapauksiin.
- Hidas muihin tietorakenteisiin verrattuna.
Lisääminen ja poistaminen:
B-puun lisäys
B-puun poisto