JOHDATUS BINÄÄRIHAKUPUUHUN - TIETORAKENTEEN JA ALGORITMIN OPETUSOHJELMAT - TECHCODEVIEW.COM

Binäärihakupuu on tietojenkäsittelytieteessä käytetty tietorakenne tietojen järjestämiseen ja tallentamiseen lajiteltuna. Binäärihakupuu seuraa kaikkia binääripuun ja sen ominaisuuksia vasemmalle lapsi sisältää arvoja, jotka ovat pienempiä kuin yläsolmu ja oikein lapsi sisältää arvoja, jotka ovat suurempia kuin yläsolmu. Tämä hierarkkinen rakenne mahdollistaa tehokkaan Etsitään , Lisäys , ja Poistaminen puuhun tallennetuille tiedoille.

Binäärihakupuu

Sisällysluettelo

java muuttumaton luettelo

Mikä on binäärihakupuu?
Binaarihakupuun ominaisuudet
Päällekkäisten arvojen käsittely binäärihakupuussa
BST:llä suoritetut toiminnot

1. Solmun etsiminen BST:stä
2. Lisää solmu BST:hen
3. Poista BST:n solmu
4. Traversal (BST:n järjestysläpikulku)

BST:n sovellukset
Edut
Haitat
Binaarihakupuun UKK (usein kysytyt kysymykset):

Mikä on binäärihakupuu?

Binäärihakupuu (BST) on erityinen tyyppi binäärinen puu jossa solmun vasemman lapsen arvo on pienempi kuin solmun arvo ja oikean lapsen arvo suurempi kuin solmun arvo. Tätä ominaisuutta kutsutaan BST-ominaisuudeksi, ja se mahdollistaa elementtien tehokkaan etsimisen, lisäämisen ja poistamisen puussa.

Binaarihakupuun ominaisuudet:

Solmun vasen alipuu sisältää vain solmut, joiden avaimet ovat pienempiä kuin solmun avain.
Solmun oikea alipuu sisältää vain solmuja, joiden avaimet ovat suuremmat kuin solmun avain.
Tämä tarkoittaa, että kaikki juuren vasemmalla puolella oleva on pienempi kuin juuren arvo ja kaikki juuren oikealla puolella oleva on suurempi kuin juuren arvo. Tämän suorituskyvyn ansiosta binäärihaku on erittäin helppoa.
Vasemman ja oikean alipuun on oltava myös binäärihakupuu.
Ei saa olla päällekkäisiä solmuja (BST:llä voi olla päällekkäisiä arvoja erilaisilla käsittelytavoilla)

Päällekkäisten arvojen käsittely binäärihakupuussa:

Meidän on noudatettava johdonmukaista prosessia koko ajan, eli joko tallennettava kaksoisarvo vasemmalle tai tallennettava kaksoisarvo juuren oikealle puolelle, mutta noudatettava lähestymistapaasi.

Binäärihakupuun perustoiminnot:

1. Solmun etsiminen BST:stä:

BST-haku tarkoittaa tietyn solmun paikantamista tietorakenteessa. Binaarihakupuussa solmun etsiminen on helppoa sen tietyn järjestyksen vuoksi. Solmun etsimisen vaiheet binaarihakupuussa on lueteltu seuraavasti -

Vertaa ensin etsittävää elementtiä puun juurielementtiin.
- Jos root täsmää kohdeelementin kanssa, palauta solmun sijainti.
- Jos se ei täsmää, tarkista onko alkio pienempi kuin juurielementti, jos se on pienempi kuin juurielementti, siirry sitten vasemmalle alipuuhun.
- Jos se on suurempi kuin juurielementti, siirry oikeaan alipuuhun.
Toista yllä olevaa toimenpidettä rekursiivisesti, kunnes vastaavuus löytyy.
Jos elementtiä ei löydy tai se ei ole puussa, palauta NULL.

Ymmärretään nyt haku binääripuussa esimerkin avulla:

Alla on annettu BST ja meidän on etsittävä elementtiä 6.

Koodi:

Alla on haun toteutus BST:ssä:

C++

// C++ function to search a given key in a given BST #include  using namespace std; struct node {  int key;  struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) {  struct node* temp  = new struct node;  temp->avain = tuote;  temp->vasen = temp->oikea = NULL;  paluulämpötila; } // Aputoiminto lisäämään // uuden solmun annetulla avaimella BST:ssä struct node* insert(struct node* node, int key) { // Jos puu on tyhjä, palauta uusi solmu if (solmu == NULL ) palauttaa newNode(avain);  // Muussa tapauksessa toista alas puussa if (avain< node->avain) solmu->vasen = insert(solmu->vasen, avain);  else if (avain> solmu->avain) solmu->oikea = insert(solmu->oikea, avain);  // Palauta (muuttumaton) solmuosoittimen palautussolmu; } // Aputoiminto avaimen etsimiseen BST:stä struct solmu* search(struct node* root, int key) root->key == avain) return root;  // Avain on suurempi kuin pääkäyttäjän avain if (root->avain< key)  return search(root->oikea, avain);  // Avain on pienempi kuin juuren avain return search(root->left, key);>>C // Java program to search a given key in a given BST class Node {  int key;  Node left, right;  public Node(int item) {  key = item;  left = right = null;  } } class BinarySearchTree {  Node root;  // Constructor  BinarySearchTree() {  root = null;  }  // A utility function to insert  // a new node with given key in BST  Node insert(Node node, int key) {  // If the tree is empty, return a new node  if (node == null) {  node = new Node(key);  return node;  }  // Otherwise, recur down the tree  if (key < node.key)  node.left = insert(node.left, key);  else if (key>solmu.avain) solmu.oikea = insert(solmu.oikea, avain);  // Palauta (muuttumaton) solmuosoittimen palautussolmu;  } // Aputoiminto avaimen etsimiseen BST-solmuhaussa (solmun juuri, int-avain) // Perustapaukset: root on null tai avain on juuressa if (root == null>
 Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>solmu.avain: solmu.oikea = insert(solmu.oikea, avain) # Palauta (muuttumaton) solmuosoittimen palautussolmu # Utility-toiminto avaimen etsimiseen BST-def-haussa(juuri, avain): # Perustapaukset: root on null tai avain on juuressa, jos root on None tai root.key == avain: return root # Avain on suurempi kuin juuren avain, jos root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
 JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) {  this.key = key;  this.left = null;  this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) {  return new Node(key); } // Otherwise, recur down the tree if (key < node.key) {  node.left = insert(node.left, key); } else if (key>solmu.avain) { solmu.oikea = insert(solmu.oikea, avain); } // Palauttaa (muuttumattomana) solmun osoittimen paluusolmun; } // Aputoiminto avaimen etsimiseen BST-funktion haussa (juuri, avain) { // Perustapaukset: root on tyhjä tai avain on juuressa if (juuri === null || root.key === avain ) { palauttaa juuri; } // Avain on suurempi kuin pääkäyttäjän avain if (root.key< key) {  return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
    
     2.         Lisää solmu BST:hen         :     
Uusi avain asetetaan aina lehteen. Aloita avaimen etsiminen juuresta lehtisolmuun. Kun lehtisolmu on löydetty, uusi solmu lisätään lehtisolmun jälkeläiseksi.
   
kuinka liittää Beats-kuulokkeet
     Koodi:    
 Alla on yhden solmun lisäyksen toteutus binäärihakupuussa:
C++ // Given Node Structure struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp = (struct node*)malloc(  sizeof(struct node));  temp->avain = tuote;  temp->vasen = temp->oikea = NULL;  paluulämpötila; } // Toiminto uuden solmun lisäämiseksi // annetulla avaimella BST:ssä struct solmu* insert(struct node* node, int key) { // Jos puu on tyhjä, palauta uusi solmu if (node == NULL) return newNode(avain);  // Muussa tapauksessa toista alas puussa if (avain< node->avain) { solmu->vasen = insert(solmu->vasen, avain);  } else if (avain> solmu->avain) { solmu->oikea = insert(solmu->oikea, avain);  } // Palauttaa solmun osoittimen paluusolmun; }>
 C // Given Node Structure struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->avain = tuote;  temp->vasen = temp->oikea = NULL;  paluulämpötila; } // Toiminto uuden solmun lisäämiseksi // annetulla avaimella BST:ssä struct solmu* insert(struct node* node, int key) { // Jos puu on tyhjä, palauta uusi solmu if (node == NULL) return newNode(avain);  // Muussa tapauksessa toista alas puussa if (avain< node->avain) { solmu->vasen = insert(solmu->vasen, avain);  } else if (avain> solmu->avain) { solmu->oikea = insert(solmu->oikea, avain);  } // Palauttaa solmun osoittimen paluusolmun; }>
 Java class GFG {  // Given Node Structure  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>solmu.avain) { solmu.oikea = insert(solmu.oikea, avain);  } // Palauttaa solmun paluusolmun;  } }>
 Python 3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>solmu.avain: solmu.oikea = insert(solmu.oikea, avain) # Palauta solmuosoittimen palautussolmu>
 Javascript // Given Node Structure class Node {  constructor(key){  this.key = key;  this.left = null;  this.right = null;  } } // Function to insert a new node with // given key in BST function insert(node, key) {    // If the tree is empty, return a new node  if (node == null)  return new Node(key);  // Otherwise, recur down the tree  if (key < node.key)  {  node.left = insert(node.left, key);  }  else if (key>solmu.avain) { solmu.oikea = insert(solmu.oikea, avain);  } // Palauttaa solmun osoittimen paluusolmun; }>
      Aika monimutkaisuus:    O(N), missä N on BST:n solmujen lukumäärä  
    Aputila:    O(1)
     3.          Poista BST:n solmu     :
Sitä käytetään tietyllä avaimella olevan solmun poistamiseen BST:stä ja uuden BST:n palauttamiseen.
 Erilaisia skenaarioita solmun poistamiseen:
     Poistettava solmu on lehtisolmu       :    
Sen yksinkertaista voit vain mitätöidä sen.
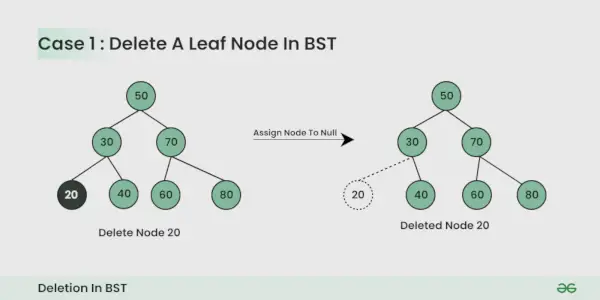
      Poistettavalla solmulla on yksi lapsi       :     
Voit vain korvata solmun lapsisolmulla.
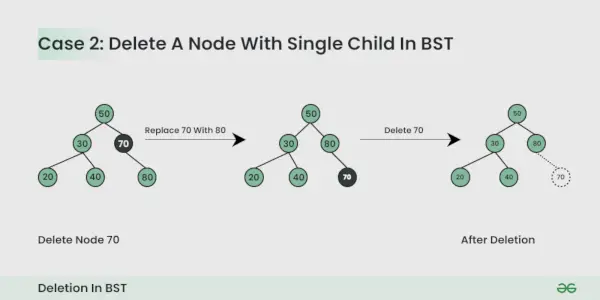
      Poistettavissa olevalla solmulla on kaksi lasta       :     
Tässä meidän täytyy    solmun poistaminen on sellainen tapa, että tuloksena oleva puu noudattaa BST:n ominaisuuksia.    Temppu on löytää solmun järjetön seuraaja. Kopioi järjestyksen seuraajan sisältö solmuun ja poista järjestyksen seuraaja.
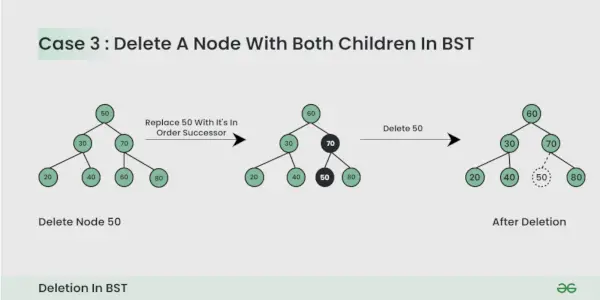
  Ota huomioon seuraavat asiat, kun poistat BST:n solmun:
 On selvitettävä, mikä poistettavan solmun tilalle tulee.
Haluat mahdollisimman vähän häiriöitä olemassa olevaan puurakenteeseen
Voi ottaa korvaavan solmun poistetuista solmuista vasemmalle tai oikealle alipuulle.
Jos otetaan jos vasemmasta alipuusta, meidän on otettava suurin arvo vasemmasta alipuusta.
Jos otetaan jos oikeasta alipuusta, meidän on otettava oikean alipuun pienin arvo.
    Koodi:    
np.unique
 Alla on poiston toteutus BST:ssä:
C++ // C++ program to delete // a node of BST // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->avain = tuote;  temp->vasen = temp->oikea = NULL;  paluulämpötila; } // Toiminto uuden solmun lisäämiseksi // annetulla avaimella BST:ssä struct solmu* insert(struct node* node, int key) { // Jos puu on tyhjä, palauta uusi solmu if (node == NULL) return newNode(avain);  // Muussa tapauksessa toista alas puussa if (avain< node->avain) { solmu->vasen = insert(solmu->vasen, avain);  } else if (avain> solmu->avain) { solmu->oikea = insert(solmu->oikea, avain);  } // Palauttaa solmun osoittimen paluusolmun; } // Funktio, joka palauttaa solmun vähimmäisarvon // avainarvolla, joka löytyy kyseisestä puusta struct solmu* minValueNode(rakennesolmu* solmu) { struct solmu* nykyinen = solmu;  // Silmukka alas löytääksesi vasemmanpuoleisen lehden, kun taas (nykyinen && nykyinen->vasen != NULL) current = nykyinen->vasen;  paluuvirta; } // Funktio, joka poistaa avaimen ja // palauttaa uuden juurirakenteen solmu* deleteNode(struct node* root, int avain) { // perustapaus if (root == NULL) return root;  // Jos poistettava avain on // pienempi kuin juuren avain, // se sijaitsee vasemmassa alipuussa if (avain< root->avain) { juuri->vasen = deleteSolmu(juuri->vasen, avain);  } // Jos poistettava avain on // suurempi kuin juuren avain, // se sijaitsee oikeanpuoleisessa alipuussa else if (avain> juuri->avain) { juuri->oikea = deleteNode(root-> oikea, avain);  } // Jos avain on sama kuin pääkäyttäjän avain, // tämä on poistettava solmu // muuten { // Solmu, jolla on vain yksi lapsi // tai ei lapsia jos (root->left == NULL) { struct solmu* temp = juuri->oikea;  vapaa(juuri);  paluulämpötila;  } else if (juuri->oikea == NULL) { struct solmu* temp = juuri->vasen;  vapaa(juuri);  paluulämpötila;  } // Solmu kahdella lapsella: // Hanki järjestyksen seuraaja(pienin // oikeanpuoleisessa alipuussa) struct solmu* temp = minValueNode(root->right);  // Kopioi järjestyksen seuraajan // sisältö tähän solmuun root->key = temp->key;  // Poista järjestyksen seuraaja root->right = deleteNode(root->right, temp->key);  } palauttaa juuri; }>
 C // C program to delete // a node of BST // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->avain = tuote;  temp->vasen = temp->oikea = NULL;  paluulämpötila; } // Toiminto uuden solmun lisäämiseksi // annetulla avaimella BST:ssä struct solmu* insert(struct node* node, int key) { // Jos puu on tyhjä, palauta uusi solmu if (node == NULL) return newNode(avain);  // Muussa tapauksessa toista alas puussa if (avain< node->avain) { solmu->vasen = insert(solmu->vasen, avain);  } else if (avain> solmu->avain) { solmu->oikea = insert(solmu->oikea, avain);  } // Palauttaa solmun osoittimen paluusolmun; } // Funktio, joka palauttaa solmun vähimmäisarvon // avainarvolla, joka löytyy kyseisestä puusta struct solmu* minValueNode(rakennesolmu* solmu) { struct solmu* nykyinen = solmu;  // Silmukka alas löytääksesi vasemmanpuoleisimman lehden, kun taas (nykyinen && nykyinen->vasen != NULL) current = nykyinen->vasen;  paluuvirta; } // Funktio, joka poistaa avaimen ja // palauttaa uuden juurirakenteen solmu* deleteNode(struct node* root, int avain) { // perustapaus if (root == NULL) return root;  // Jos poistettava avain on // pienempi kuin juuren avain, // se sijaitsee vasemmassa alipuussa if (avain< root->avain) { juuri->vasen = deleteSolmu(juuri->vasen, avain);  } // Jos poistettava avain on // suurempi kuin juuren avain, // se sijaitsee oikeanpuoleisessa alipuussa else if (avain> juuri->avain) { juuri->oikea = deleteNode(root-> oikea, avain);  } // Jos avain on sama kuin pääkäyttäjän avain, // tämä on poistettava solmu // muuten { // Solmu, jolla on vain yksi lapsi // tai ei lapsia jos (root->left == NULL) { struct solmu* temp = juuri->oikea;  vapaa(juuri);  paluulämpötila;  } else if (juuri->oikea == NULL) { struct solmu* temp = juuri->vasen;  vapaa(juuri);  paluulämpötila;  } // Solmu kahdella lapsella: // Hanki järjestyksen seuraaja(pienin // oikeanpuoleisessa alipuussa) struct solmu* temp = minValueNode(root->right);  // Kopioi järjestyksen seuraajan // sisältö tähän solmuun root->key = temp->key;  // Poista järjestyksen seuraaja root->right = deleteNode(root->right, temp->key);  } palauttaa juuri; }>
 Java // Java program for Delete a Node of BST class GFG {  // Given Node node  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>solmu.avain) { solmu.oikea = insert(solmu.oikea, avain);  } // Palauttaa solmun paluusolmun;  } // Funktio, joka palauttaa solmun minimaalisella //-avainarvolla, joka löytyy kyseisestä puusta staattinen solmu minValueNode(solmusolmu) { solmun nykyinen = solmu;  // Silmukka alas löytääksesi vasemmanpuoleisen lehden, kun (current != null && current.left != null) current = current.left;  paluuvirta;  } // Funktio, joka poistaa avaimen ja // palauttaa uuden staattisen juurisolmun deleteNode(solmun juuri, int avain) { // perustapaus if (root == null) return root;  // Jos poistettava avain on // pienempi kuin juuren avain, // se sijaitsee vasemmassa alipuussa if (avain< root.key) {  root.left = deleteNode(root.left, key);  }  // If the key to be deleted is  // greater than the root's key,  // then it lies in right subtree  else if (key>juuri.avain) { juuri.oikea = deleteSolmu(juuri.oikea, avain);  } // Jos avain on sama kuin pääkäyttäjän avain, // tämä on poistettava solmu // muuten { // Solmu, jolla on vain yksi lapsi // tai ei lapsia if (root.left == null) { solmun lämpötila = root.right;  paluulämpötila;  } else if (root.right == null) { solmun temp = root.left;  paluulämpötila;  } // Solmu kahdella lapsella: // Hanki järjestyksen seuraaja(pienin // oikeanpuoleisessa alipuussa) solmu temp = minValueNode(root.right);  // Kopioi järjestyksen seuraajan // sisältö tähän solmuun root.key = temp.key;  // Poista järjestyksen seuraaja root.right = deleteNode(root.right, temp.key);  } palauttaa juuri;  }>
 Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Palauta solmun osoitin return root # Toiminto BST:n inorder-läpikulkuun tekemiseksi def inorder(root): if root: inorder(root.left) print(root. avain, end=' ') inorder(root.right) # Funktio, joka palauttaa solmun, jonka # minimiarvo löytyy kyseisestä puusta def minValueNode(node): current = node # Silmukka alas löytääksesi vasemmanpuoleisen lehden, kun nykyinen ja current.left ei ole None: current = current.left return current # Funktio, joka poistaa avaimen ja # palauttaa uuden päätyypin def deleteSolmu(juuri, avain): # perustapaus, jos root on Ei mitään: return root # Jos avain on deleted on # pienempi kuin juuren avain, # sitten se sijaitsee vasemmassa alipuussa if key< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteSolmu(juuri.oikea, avain) # Jos avain on sama kuin pääkäyttäjän avain, # niin tämä on poistettava solmu # muuten: # Solmu jossa vain yksi lapsi # tai ei avain if root.left on Ei mitään: temp = root.right root = Ei mitään paluu temp elif root.right on Ei mitään: temp = root.left root = Ei mitään paluulämpötila # Solmu, jossa on kaksi lasta: # Hanki järjestyksen seuraaja(pienin # oikea alipuu) temp = minValueNode(root.right) # Kopioi järjestyksen seuraajan # sisältö tähän solmuun root.key = temp.key # Poista järjestyksen seuraaja root.right = deleteNode(root.right, temp.key) palauta juuri>
      4.         Traversal (BST:n järjestysläpikulku)         :    
Binäärihakupuiden (BST) tapauksessa Inorder traversal antaa solmut ei-laskevassa järjestyksessä. Vierailemme ensin vasemman lapsen, sitten juuren ja sitten oikean lapsen luona.
 Alla on binäärihakupuun läpikulku:
C++ // C++ program to implement // inorder traversal of BST #include  using namespace std; // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp = (struct node*)malloc(  sizeof(struct node));  temp->avain = tuote;  temp->vasen = temp->oikea = NULL;  paluulämpötila; } // Toiminto uuden solmun lisäämiseksi // annetulla avaimella BST:ssä struct solmu* insert(struct node* node, int key) { // Jos puu on tyhjä, palauta uusi solmu if (node == NULL) return newNode(avain);  // Muussa tapauksessa toista alas puussa if (avain< node->avain) { solmu->vasen = insert(solmu->vasen, avain);  } else if (avain> solmu->avain) { solmu->oikea = insert(solmu->oikea, avain);  } // Palauttaa solmun osoittimen paluusolmun; } // Funktio BST:n inorder läpikulkuun void inorder(struct solmu* root) { if (juuri != NULL) { inorder(root->left);  cout<< ' ' << root->avain;  inorder(juuri->oikea);  } } // Ohjainkoodi int main() { /* Luodaan seuraava BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // BST-juuren luominen = insert(root, 50);  insert(juuri, 30);  insert(juuri, 20);  insert(juuri, 40);  insert(juuri, 70);  insert(juuri, 60);  insert(juuri, 80);  // Toiminto Kutsu inorder(root);  paluu 0; } // Tämän koodin tarjoaa shivanisinghss2110>
 C // C program to implement // inorder traversal of BST #include  #include  // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->avain = tuote;  temp->vasen = temp->oikea = NULL;  paluulämpötila; } // Toiminto uuden solmun lisäämiseksi // annetulla avaimella BST:ssä struct solmu* insert(struct node* node, int key) { // Jos puu on tyhjä, palauta uusi solmu if (node == NULL) return newNode(avain);  // Muussa tapauksessa toista alas puussa if (avain< node->avain) { solmu->vasen = insert(solmu->vasen, avain);  } else if (avain> solmu->avain) { solmu->oikea = insert(solmu->oikea, avain);  } // Palauttaa solmun osoittimen paluusolmun; } // Funktio BST:n inorder läpikulkuun void inorder(struct solmu* root) { if (juuri != NULL) { inorder(root->left);  printf('%d ', root->avain);  inorder(juuri->oikea);  } } // Ohjainkoodi int main() { /* Luodaan seuraava BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // BST-juuren luominen = insert(root, 50);  insert(juuri, 30);  insert(juuri, 20);  insert(juuri, 40);  insert(juuri, 70);  insert(juuri, 60);  insert(juuri, 80);  // Toiminto Kutsu inorder(root);  paluu 0; }>
 Java import java.io.*; // Java program for Inorder Traversal class GFG {  // Given Node node  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>solmu.avain) { solmu.oikea = insert(solmu.oikea, avain);  } // Palauttaa solmun paluusolmun;  } // Toiminto BST:n inorder-läpiviennille static void inorder(solmun juuri) { if (juuri != null) { inorder(root.left);  System.out.print(' ' + root.key);  inorder(root.right);  } } // Ohjainkoodi public static void main(String[] args) { /* Luodaan seuraava BST 50 /  30 70 /  /  20 40 60 80 */ node root = null;  // arvon lisääminen 50 root = insert(juuri, 50);  // arvon lisääminen 30 insert(root, 30);  // arvon lisääminen 20 insert(root, 20);  // arvon lisääminen 40 insert(root, 40);  // arvon lisääminen 70 insert(root, 70);  // arvon lisääminen 60 insert(root, 60);  // arvon lisääminen 80 insert(root, 80);  // tulostaa BST inorder(root);  } } // Tämän koodin tarjoaa abhijitjadhav1998>
 Python 3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>solmu.avain: solmu.oikea = insert(solmu.oikea, avain) # Palauta solmuosoittimen paluusolmu # Toiminto, jolla tehdään BST:n inorder-läpikulku inorder(root): if root: inorder(root.left) print(root. avain, end=' ') inorder(root.right) # Ohjainkoodi if __name__ == '__main__': # Luodaan seuraava BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 juuri = Ei mitään # BST-juuren luominen = insert(juuri, 50) insert(juuri, 30) insert(juuri, 20) insert(juuri, 40) insert(juuri, 70) insert(juuri, 60) insert(juuri) , 80) # Toiminto Kutsu inorder(root) #Tämän koodin tarjoaa japmeet01>
   
  Lähtö   20 30 40 50 60 70 80>
     Aika monimutkaisuus:    O(N), missä N on BST:n solmujen lukumäärä  
    Aputila:    O(1)
     BST:n sovellukset:    
    Graafialgoritmit:    BST:itä voidaan käyttää graafialgoritmien toteuttamiseen, kuten minimivirittävän puun algoritmeihin.
    Prioriteettijonot:    BST:illä voidaan toteuttaa prioriteettijonoja, joissa korkeimman prioriteetin elementti on puun juuressa ja alipuihin tallennetaan alempiin prioriteetteihin kuuluvat elementit.
    Itsetasapainottava binäärihakupuu:    BST:itä voidaan käyttää itsetasapainottavina tietorakenteina, kuten AVL-puu ja punainen-musta puu.
    Tietojen tallennus ja haku:    BST:itä voidaan käyttää tietojen nopeaan tallentamiseen ja hakemiseen, esimerkiksi tietokantoihin, joissa tietyn tietueen etsiminen voidaan tehdä logaritmisajassa.
    Edut:    
    Nopea haku:    Tietyn arvon etsimisen BST:stä keskimääräinen aikakompleksisuus on O(log n), missä n on puun solmujen lukumäärä. Tämä on paljon nopeampaa kuin elementin etsiminen taulukosta tai linkitetystä listasta, jonka aikamonimutkaisuus on pahimmassa tapauksessa O(n).
    Tilauskierros:    BST:t voidaan kulkea järjestyksessä, joka vierailee vasemmassa alipuussa, juurissa ja oikeassa alipuussa. Tätä voidaan käyttää tietojoukon lajitteluun.
    Tilatehokas:    BST:t ovat tilaa säästäviä, koska ne eivät tallenna ylimääräistä tietoa, toisin kuin taulukot ja linkitetyt luettelot.
    Haitat:    
    Vinossa olevat puut:    Jos puu vääristyy, haku-, lisäys- ja poistotoimintojen aikamonimutkaisuus on O(n) O(log n) sijaan, mikä voi tehdä puusta tehottoman.
    Tarvittava lisäaika:    Itsetasapainottavat puut vaativat lisäaikaa säilyttääkseen tasapainon lisäys- ja poistotoimintojen aikana.
    Tehokkuus:    BST:t eivät ole tehokkaita tietojoukoissa, joissa on useita kaksoiskappaleita, koska ne tuhlaavat tilaa.
FAQ:t(Usein Kysytyt Kysymykset)binäärihakupuussa:
    1. Mikä on binäärihakupuu?    
 Binäärihakupuu (BST) on    binääripuu, jossa jokainen solmu vasemmassa alipuussa on pienempi kuin juuri ja jokainen solmu oikean alipuussa on arvoa suurempi kuin juuri    . Binaarihakupuun ominaisuudet ovat rekursiivisia: jos katsomme mitä tahansa solmua juurina, nämä ominaisuudet pysyvät totta.
 
2. Mikä on binäärihakupuuoperaatio?
 Binäärihakupuussa on kolme päätoimintoa:    1. Lisäys, 2. Poistaminen, 3. Haku.    Ominaisuuksiensa vuoksi se on tehokas etsiä mitä tahansa elementtiä binaarihakupuussa.
 
3. Mikä on binäärihakupuu ja AVL-puu?
     Binäärihakupuu       :    Binäärihakupuu (BST) on binääripuu, jossa jokainen vasemman alipuun solmu on pienempi kuin juuri ja jokaisen oikean alipuun solmun arvo on suurempi kuin juuri.
     AVL puu       :    Binäärihakupuut (BST), jotka tasapainottavat ja pyörivät automaattisesti, tunnetaan AVL-puina.
 
4. Mitä binaarihakupuuta käytetään?
 Binaarihakupuiden avulla voidaan toteuttaa abstrakteja tietotyyppejä, kuten    dynaamiset joukot, hakutaulukot ja prioriteettijonot,    ja käytetty    lajittelualgoritmit    kuten puulajittelu.
 
5. Mitä eroa on binäärihakupuulla ja binääripuulla?
 Binäärihakupuu on puu, joka noudattaa tiettyä järjestystä elementtien järjestämisessä, kun taas binääripuu ei seuraa mitään järjestystä.
 
    Aiheeseen liittyvät artikkelit:    
      BST:n soveltaminen     
     Binaarihakupuun sovellukset, edut ja haitat     
     Lisäys binaarihakupuuhun (BST)     
     Haku binäärihakupuusta (BST)     
     Poisto binäärihakupuussa (BST)

TechCodeview

Johdatus binäärihakupuuhun – tietorakenteen ja algoritmin opetusohjelmat

Mikä on binäärihakupuu?

Binaarihakupuun ominaisuudet:

Päällekkäisten arvojen käsittely binäärihakupuussa:

Binäärihakupuun perustoiminnot:

1. Solmun etsiminen BST:stä:

2. Lisää solmu BST:hen :

3. Poista BST:n solmu :

Poistettava solmu on lehtisolmu :

Poistettavalla solmulla on yksi lapsi :

Poistettavissa olevalla solmulla on kaksi lasta :

4. Traversal (BST:n järjestysläpikulku) :

BST:n sovellukset:

Edut:

Haitat:

FAQ:t(Usein Kysytyt Kysymykset)binäärihakupuussa:

1. Mikä on binäärihakupuu?

2. Mikä on binäärihakupuuoperaatio?

3. Mikä on binäärihakupuu ja AVL-puu?

4. Mitä binaarihakupuuta käytetään?

5. Mitä eroa on binäärihakupuulla ja binääripuulla?