Koska a BST , tehtävänä on etsiä solmu tästä BST .
Jos haluat etsiä arvoa BST:stä, pidä sitä lajiteltuna taulukkona. Nyt voimme helposti suorittaa hakutoiminnon BST:ssä käyttämällä Binäärihakualgoritmi .
Algoritmi avaimen etsimiseksi tietystä binäärihakupuusta:
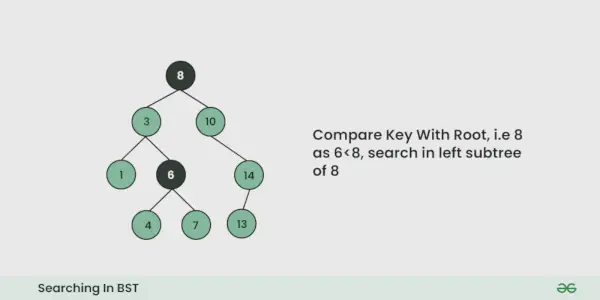
Oletetaan, että haluamme etsiä numeroa X, Aloitamme juuresta. Sitten:
- Vertaamme haettavaa arvoa juuren arvoon.
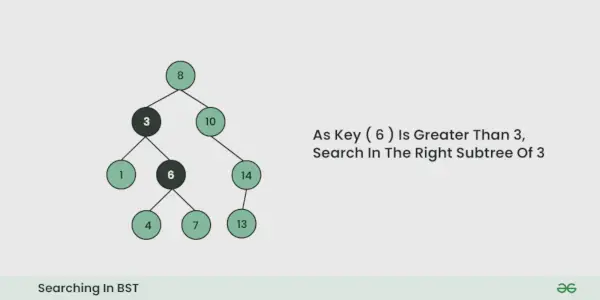
- Jos se on yhtä suuri, olemme tehneet haun, jos se on pienempi, tiedämme, että meidän on siirryttävä vasempaan alipuuhun, koska binäärihakupuussa kaikki vasemman alipuun elementit ovat pienempiä ja kaikki oikean alipuun elementit ovat suurempia.
- Toista yllä oleva vaihe, kunnes se ei enää ole mahdollista
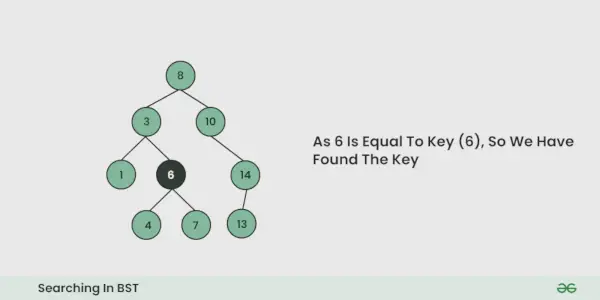
- Jos avain löytyy jossain iteraatiossa, palauta True. Muuten vääriä.
Kuva hausta BST:ssä:
Katso alla oleva kuva ymmärtääksesi paremmin:
Suositeltu käytäntöHae solmu BSTT:stä Kokeile sitä!
lista lajiteltu java
Ohjelma haun toteuttamiseksi BST:ssä:
C++
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >=>new> struct> node;> >temp->avain = tuote;> >temp->vasen = temp->right = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->vasen = insert(solmu->vasen, avain);> >else> if> (key>solmu->avain)> >node->oikea = insert(solmu->oikea, avain);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > >// Base Cases: root is null or key is present at root> >if> (root == NULL> // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >return> 0;> }> |
>
>
C
// C function to search a given key in a given BST> #include> #include> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >= (>struct> node*)>malloc>(>sizeof>(>struct> node));> >temp->avain = tuote;> >temp->vasen = temp->right = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->vasen = insert(solmu->vasen, avain);> >else> if> (key>solmu->avain)> >node->oikea = insert(solmu->oikea, avain);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >return> 0;> }> |
>
>
Java
tiedostopääte java
// Java program to search a given key in a given BST> class> Node {> >int> key;> >Node left, right;> >public> Node(>int> item) {> >key = item;> >left = right =>null>;> >}> }> class> BinarySearchTree {> >Node root;> >// Constructor> >BinarySearchTree() {> >root =>null>;> >}> >// A utility function to insert> >// a new node with given key in BST> >Node insert(Node node,>int> key) {> >// If the tree is empty, return a new node> >if> (node ==>null>) {> >node =>new> Node(key);> >return> node;> >}> >// Otherwise, recur down the tree> >if> (key node.left = insert(node.left, key); else if (key>solmu.avain) solmu.oikea = insert(solmu.oikea, avain); // Palauta (muuttumaton) solmuosoittimen palautussolmu; } // Aputoiminto avaimen etsimiseen BST-solmun haussa(solmun juuri, int avain) // Ohjainkoodi public static void main(String[] args) { BinarySearchTree tree = new BinarySearchTree(); // Solmujen lisääminen tree.root = puu.insert(puu.juuri, 50); puu.insert(puu.juuri, 30); puu.insert(puu.juuri, 20); puu.insert(puu.juuri, 40); puu.insert(puu.juuri, 70); puu.insert(puu.juuri, 60); puu.insert(puu.juuri, 80); // Löydettävä avain int avain = 6; // Haku BST:stä if (tree.search(tree.root, key) == null) System.out.println(avain + ' ei löydy'); else System.out.println(näppäin + ' löydetty'); avain = 60; // Haku BST:stä if (tree.search(tree.root, key) == null) System.out.println(avain + ' ei löydy'); else System.out.println(näppäin + ' löydetty'); } }> |
>
>
Python 3
# Python3 function to search a given key in a given BST> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> ># If the tree is empty, return a new node> >if> node>is> None>:> >return> Node(key)> ># Otherwise, recur down the tree> >if> key node.left = insert(node.left, key) elif key>solmu.avain: solmu.oikea = insert(solmu.oikea, avain) # Palauta (muuttumaton) solmuosoittimen palautussolmu # Utility-toiminto avaimen etsimiseen BST-def-haussa(juuri, avain): # Perustapaukset: root on null tai avain on juuressa, jos root on None tai root.key == avain: return root # Avain on suurempi kuin rootin avain jos root.key return search(root.right, key) # Avain on pienempi kuin root 's key return search(root.left, key) # Ohjainkoodi if __name__ == '__main__': root = Ei mitään root = insert(juuri, 50) insert(juuri, 30) insert(juuri, 20) insert (juuri, 40) insert(juuri, 70) insert(juuri, 60) insert(juuri, 80) # Löydettävä avain = 6 # Haku BST:stä, jos haku(juuri, avain) on Ei mitään: print(avain, 'ei löydy') else: print(avain, 'löyty') avain = 60 # Haku BST:stä, jos haku(juuri, avain) on Ei mitään: print(avain, 'ei löydy') else: print(avain, 'löyty')> |
>
>
C#
// C# function to search a given key in a given BST> using> System;> public> class> Node {> >public> int> key;> >public> Node left, right;> }> public> class> BinaryTree {> >// A utility function to create a new BST node> >public> Node NewNode(>int> item)> >{> >Node temp =>new> Node();> >temp.key = item;> >temp.left = temp.right =>null>;> >return> temp;> >}> >// A utility function to insert> >// a new node with given key in BST> >public> Node Insert(Node node,>int> key)> >{> >// If the tree is empty, return a new node> >if> (node ==>null>)> >return> NewNode(key);> >// Otherwise, recur down the tree> >if> (key node.left = Insert(node.left, key); else if (key>solmu.avain) solmu.oikea = Insert(solmu.oikea, avain); // Palauta (muuttumaton) solmuosoittimen palautussolmu; } // Aputoiminto avaimen etsimiseen BST:n julkisesta solmuhausta (solmun juuri, int avain) // Perustapaukset: root on null tai avain on juuressa if (root == null // Ohjainkoodi public static void Main () { BinaryTree bt = new BinaryTree(root, 50); , 40; bt.Insert(root, 60); bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(avain + ' avain = 60); if (bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(key + ' found' } }>'>); |
>
// Javascript function to search a given key in a given BST>class Node {>>constructor(key) {>>this>.key = key;>>this>.left =>null>;>>this>.right =>null>;>>}>}>// A utility function to insert>// a new node with given key in BST>function>insert(node, key) {>>// If the tree is empty, return a new node>>if>(node ===>null>) {>>return>new>Node(key);>>}>>// Otherwise, recur down the tree>>if>(key node.left = insert(node.left, key); } else if (key>solmu.avain) { solmu.oikea = insert(solmu.oikea, avain); } // Palauttaa (muuttumattomana) solmun osoittimen paluusolmun; } // Aputoiminto avaimen etsimiseen BST-funktion haussa (juuri, avain) { // Perustapaukset: root on tyhjä tai avain on juuressa if (juuri === null || root.key === avain ) { palauttaa juuri; } // Avain on suurempi kuin juuren avain if (root.key return search(root.right, key); } // Avain on pienempi kuin rootin avain return search(root.left, avain); } // Driver Code let root = insert(root, 30 insert(root, 70); 60 insert(root, 80); löytyi');} else { console.log(key + ' found' } key = 60 // Etsitään BST:stä if (search(root, key) === null) { console.log(; key + ' not found'); } else { console.log(key + ' found' }>'>).tuplaa javassa>6 not found 60 found> Aika monimutkaisuus: O(h), missä h on BST:n korkeus.
Aputila: O(h), missä h on BST:n korkeus. Tämä johtuu siitä, että rekursiopinon tallentamiseen tarvittava tilan enimmäismäärä olisi h .Liittyvät linkit:
- Binäärihakupuun lisäystoiminto
- Binäärihakupuun poistotoiminto