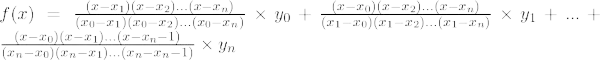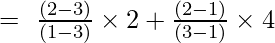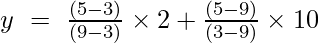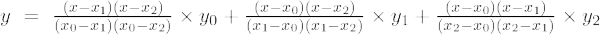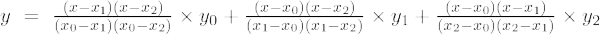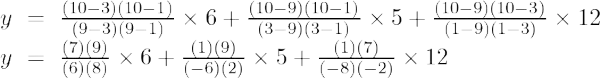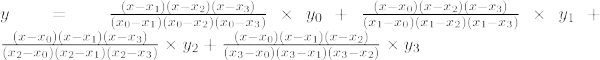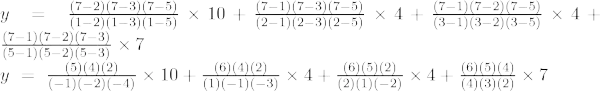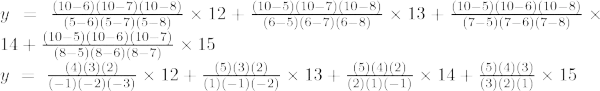logo

TechCodeview

Lagrangen interpolointikaava

Lagrangen interpolointikaava löytää polynomin nimeltä Lagrangen polynomi, joka saa tietyt arvot mielivaltaisessa pisteessä. Se on n-aste funktion f(x) polynomilauseke. Interpolointimenetelmää käytetään uusien datapisteiden etsimiseen tunnettujen datapisteiden diskreetin joukon alueelta.

Tässä artikkelissa opimme Lagrangen interpolaatiosta, Lagrangen interpolaatiokaavasta, Lagrangen interpolaatiokaavan todistuksesta, Lagrangen interpolaatiokaavaan perustuvista esimerkeistä ja muista yksityiskohtaisesti.



Mikä on Lagrangen interpolointi?

Lagrange-interpolointi on tapa löytää minkä tahansa funktion arvo missä tahansa pisteessä, kun funktiota ei ole annettu. Käytämme funktion muita pisteitä saadaksemme funktion arvon missä tahansa vaaditussa pisteessä.

Oletetaan, että meillä on funktio y = f(x), jossa x:n arvojen korvaaminen antaa eri arvoja y:lle. Ja meille annetaan kaksi pistettä (x1, ja1) ja (x2, ja2) käyrällä, niin y:n arvo kohdassa x = a(vakio) lasketaan Lagrangen interpolaatiokaavalla.

Lagrangen interpolointikaava

Annettu muutama reaaliarvo x1, x2, x3, …, xnja y1, ja2, ja3, … janja tulee olemaan polynomi P, jonka todelliset kertoimet täyttävät ehdot P(xi) = jai, ∀ i = {1, 2, 3, …, n} ja polynomin P asteen on oltava pienempi kuin todellisten arvojen lukumäärä, eli aste(P)



Lagrangen interpolointikaava n:nnelle kertaluvulle

Lagrangen interpolaatiokaava n:llethasteen polynomi on annettu alla:

Lagrangen interpolointikaava n:lle th järjestys on,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n



Lagrangen ensimmäisen asteen interpolointikaava

Jos Polynomin aste on 1, jolloin sitä kutsutaan ensimmäisen asteen polynomiksi. Lagrangen interpolointikaava 1stpolynomien järjestys on,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Lagrangen toisen asteen interpolointikaava

Jos polynomin aste on 2, sitä kutsutaan toisen asteen polynomiksi. Lagrangen interpolointikaava 2. kertaluvun polynomeille on,

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Lagrangen lauseen todiste

Tarkastellaan annetun muodon n:nnen asteen polynomia,

f(x) = A0(x-x1)(x – x2)(x – x3)…(x – xn) + A1(x-x1)(x – x2)(x – x3)…(x – xn) + … + A(n-1)(x-x1)(x – x2)(x – x3)…(x – xn)

Korvaa havainnot xisaadakseen Ai

Laita x = x0sitten saamme A0

f(x0) = ja0= A0(x0– x1)(x0– x2)(x0– x3)…(x0– xn)

A 0 = ja 0 /(x 0 – x 1 )(x 0 – x 2 )(x 0 – x 3 )…(x 0 – x n )

Korvaamalla x = x1saamme A1

diana mary blacker

f(x1) = ja1= A1(x1– x0)(x1– x2)(x1– x3)…(x1– xn)

A 1 = ja 1 /(x 1 – x 0 )(x 1 – x 2 )(x 1 – x 3 )…(x 1 – x n )

Vastaavasti korvaamalla x = xnsaamme An

f(xn) = jan= An(xn– x0)(xn– x1)(xn– x2)…(xn– xn-1)

A n = ja n /(x n – x 0 )(x n – x 1 )(x n – x 2 )…(x n – x n-1 )

Jos korvaamme kaikki A:n arvotifunktiossa f(x), jossa i = 1, 2, 3, …n, niin saadaan Lagrangen interpolaatiokaava:

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} kertaa y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Lagrangen interpolointikaavan ominaisuudet

Lagrangen interpolaatiokaavan eri ominaisuuksia käsitellään alla,

  • Tätä kaavaa käytetään funktion arvon löytämiseen missä tahansa pisteessä, vaikka itse funktiota ei olisi annettu.
  • Sitä käytetään, vaikka annetut pisteet eivät olisikaan tasaisin välein.
  • Se antaa riippumattoman muuttujan arvon mille tahansa riippumattomalle muuttujalle, joka kuuluu mihin tahansa funktioon, ja siksi sitä käytetään Numeracial Analysisissä funktion arvojen etsimiseen jne.

Lagrangen interpolointikaavan käyttötarkoitukset

Lagrangen interpolaatiokaavan eri käyttötapoja käsitellään alla,

  • Sitä käytetään riippuvan muuttujan arvon löytämiseen missä tahansa riippumattomassa muuttujassa, vaikka itse funktiota ei olisi annettu.
  • Sitä käytetään kuvan skaalauksessa.
  • Sitä käytetään AI-mallinnuksessa.
  • Sitä käytetään opettamaan NLP: tä jne.

Lue lisää,

  • Interpolointikaava
  • Lineaarinen interpolaatiokaava

Esimerkkejä Lagrangen interpolointikaavan käytöstä

Katsotaanpa muutama esimerkkikysymys Lagrangen interpolaatiokaavasta.

Esimerkki 1: Etsi y:n arvo kohdassa x = 2 annetulle pistejoukolle (1, 2), (3, 4)

Ratkaisu:

Annettu,

  • (x0, ja0) = (1, 2)
  • (x1, ja1) = (3, 4)

Ensimmäisen kertaluvun Lagrangen interpolointikaava on,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Kun x = 2

ja =~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Y:n arvo kohdassa x = 2 on 3

Esimerkki 2: Etsi y:n arvo kohdassa x = 5 annetulle pistejoukolle (9, 2), (3, 10)

Ratkaisu:

Annettu,

  • (x0, ja0) = (9, 2)
  • (x1, ja1) = (3, 10)

Ensimmäisen kertaluvun Lagrangen interpolointikaava on,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Kun x = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Y:n arvo kohdassa x = 5 on 7,33

Esimerkki 3: Etsi y:n arvo kohdassa x = 1 annetulle pistejoukolle (1, 6), (3, 4), (2, 5)

Ratkaisu:

Annettu,

  • (x0, ja0) = (1, 6)
  • (x1, ja1) = (3, 4)
  • (x2, ja2) = (2, 5)

Toisen asteen Lagrangen interpolaatiokaava on,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Kun x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)}kertaa 4+frac{(1-1)(1-3)}{(2-1)(2-3)}kertaa 5 y~=~ murto{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)}kertaa 5

y = (12/2) + 0 + 0

y = 6

Y:n arvo kohdassa x = 1 on 6

Esimerkki 4: Etsi y:n arvo kohdassa x = 10 annetulle pistejoukolle (9, 6), (3, 5), (1, 12)

Ratkaisu:

Annettu,

  • (x0, ja0) = (9, 6)
  • (x1, ja1) = (3, 5)
  • (x2, ja2) = (1, 12)

Toisen asteen Lagrangen interpolaatiokaava on,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Kun x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)}kertaa 5+frac{(10-9)(10-3)}{(1-9)(1-3)}kertaa 12 y~=~ murto{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)} imes 12

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Y:n arvo kohdassa x = 10 on 9,375

Esimerkki 5: Etsi y:n arvo kohdassa x = 7 annetulle pistejoukolle (1, 10), (2, 4), (3, 4), (5, 7)

Ratkaisu:

Annettu,

  • (x0, ja0) = (1, 10)
  • (x1, ja1) = (2, 4)
  • (x2, ja2) = (3, 4)
  • (x3, ja3) = (5, 7)

Kolmannen asteen Lagrangen interpolaatiokaava on,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)}kertaa y_3

Kun x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)}kertaa 10+frac{(7-) 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)}kertaa 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)}kertaa 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)}kertaa 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)}kertaa 4+frac{(6)(5)(4)}{(4)(3)(2)}kertaa 7

y = -50 + 64 – 60 + 35

y = 99–110 = -yksitoista

Y:n arvo kohdassa x = 7 on -11

Esimerkki 6: Etsi y:n arvo kohdassa x = 10 annetulle pistejoukolle (5, 12), (6, 13), (7, 14), (8, 15)

Ratkaisu:

Annettu,

  • (x0, ja0) = (5, 12)
  • (x1, ja1) = (6, 13)
  • (x2, ja2) = (7, 14)
  • (x3, ja3) = (8, 15)

Kolmannen asteen Lagrangen interpolaatiokaava on,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)}kertaa y_3

Kun x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)}kertaa 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)}kertaa 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)}kertaa 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)}kertaa 14+frac{(5)(4)(3)}{(3)(2)(1)}kertaa 15

y = -48 + 195 – 280 + 150

y = 17

Y:n arvo, kun x = 10, on 17

Esimerkki 7: Etsi y:n arvo kohdassa x = 0 annetulle pistejoukolle (-2, 5), (1, 7)

Ratkaisu:

Annettu,

  • (x0, ja0) = (-2, 5)
  • (x1, ja1) = (1, 7)

Ensimmäisen asteen Lagrangen interpolointikaava on,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Kun x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Y:n arvo kohdassa x = 0 on 6,33

Lagrangen interpolointikaavaa koskevat usein kysytyt kysymykset

1. Mikä on Lagrangen interpolointikaava?

Lagrangen interpolointikaava on kaava, jota käytetään funktion riippuvan muuttujan arvon löytämiseen mille tahansa riippumattomalle muuttujalle, vaikka itse funktiota ei ole annettu.

2. Mitkä ovat Lagrangen interpolointikaavan sovellukset?

Lagranges Formulalla on useita sovelluksia nykyaikaisessa matematiikassa ja tietotieteissä,

  • Sitä käytetään AI-malliin Traning.
  • Sitä käytetään kuvankäsittelyssä.
  • Sitä käytetään kolmiulotteisten ja korkeampien käyrien kuvaamiseen jne.

3. Mikä on ensimmäisen asteen Lagrangen interpolointikaava?

Ensimmäisen asteen Lagranges-interpolaatiokaava on,

f(x) = (x – x 1 )/(x 0 – x 1 )×f 0 + (x – x 0 )/(x 1 – x 0 )×f 1

4. Mikä on toisen asteen Lagrangen interpolointikaava?

Toisen asteen Lagranges-interpolaatiokaava on,

f(x) = [(x – x 1 )(x – x 2 )/(x 0 – x 1 )(x 0 – x 2 )]×f 0 + [(x – x 0 )(x – x 2 )/(x 1 – x 0 )(x 1 – x 2 )]×f 1 + [(x – x 0 )(x – x 1 )/(x 2 – x 0 )(x 2 – x 2 )]×f 0