Fysiikassa suuruus tarkoittaa kohteen maksimikokoa ja suuntaa. Sitä käytetään sekä vektori- että skalaarisuureissa yhteisenä tekijänä. Esimerkiksi skalaarisuureella on vain suuruus, sillä ei ole tai vaadita suuntaa itsensä kuvaamiseen.

k klusterointialgoritmi

Magnituden avulla voimme vertailla eri liikkuvien kohteiden nopeutta, liikkuvan kohteen kulkemaa etäisyyttä ja myös kertoo kohteen määrän.

Esimerkiksi kun kyseessä on liikkuva auto, joka liikkuu nopeammin kuin moottoripyörä, auton nopeuden suuruus on suurempi kuin moottoripyörän nopeuden suuruus. Fysiikassa on kahdenlaisia ​​​​suureita: skalaari ja vektori.

Skalaarisuureella, kuten nopeudella, on vain suuruus, ei suunta. Sitä vastoin vektorisuureella on sekä suuruus että suunta, kuten nopeus. Tässä on joitain tapoja, joilla suuruusluokkaa käytetään:

• Maanjäristyksen voimakkuus
• Elektronin varauksen suuruus
• Gravitaatiovoiman suuruus
• Voiman suuruus, siirtymä jne.

1. Maanjäristyksen voimakkuus:

Maanjäristyksen voimakkuus määritellään pituudella, leveydellä ja leveydellä. Voimme sanoa, että se viittaa maanjäristyksen fyysiseen kokoon. Se aiheuttaa erilaista tärinää eri paikoissa, mikä johtuu pintamateriaalin tyypistä ja etäisyydestä episentrumista. Sen suuruus on merkitty kokonaisluvuilla, mukaan lukien desimaalimurtoluvut. Maanjäristys, jonka voimakkuus on 5,3, katsotaan kohtalaiseksi maanjäristykseksi ja voimakkaaksi, jos voimakkuus on 6 tai enemmän.

Maanjäristyksen sattuessa vapautuu suuri määrä energiaa, joka aiheuttaa seismiset aallot, jotka kulkevat kaikkiin suuntiin ja ravistelevat maata ja aiheuttavat tuhoa. Maanjäristyksen voimakkuus auttaa ennustamaan sen esiintymisen todennäköisyyttä tulevaisuudessa. Asteikkoa, joka mittaa maanjäristyksen voimakkuutta, kutsutaan Richterin asteikoksi. Tällä asteikolla jokaisella luvun kasvulla suuruus kasvaa kymmenen kertaa.

2. Elektronin varauksen suuruus

Elektronin varaus on yhtä suuri kuin alkuainevarauksen suuruus, e negatiivisella etumerkillä. Esimerkiksi 1,602 x 10^-19. Lisäksi on olemassa kahdenlaisia ​​sähkövarauksia: positiivisia ja negatiivisia. Protoneissa on positiivinen varaus ja elektroneissa negatiivinen varaus. Atomin nettovarauksen sanotaan olevan positiivinen, jos siinä on enemmän protoneja kuin elektroneja. Vastaavasti, jos atomilla on negatiivinen varaus, jos elektroneja on enemmän kuin protoneja. Kun siinä on yhtä monta elektronia ja protoneja, sen sanotaan olevan sähköisesti neutraali.

3. Voiman suuruus

Se viittaa kaikkien esineeseen vaikuttavien voimien summaan. Jos kaikki voimat vaikuttavat samaan suuntaan, se lisää voiman suuruutta. Jos nämä voimat vaikuttavat eri suuntiin, voiman suuruus pienenee, kun vastakkaisiin suuntiin vaikuttavat voimat kumoavat tai neutraloivat toistensa vaikutuksen.

4. Siirtymän suuruus

Siirtymä tarkoittaa lyhintä mahdollista etäisyyttä kohteen alku- ja loppuasennon välillä. Liikkuvan kohteen siirtymän suuruus on aina joko pienempi tai yhtä suuri kuin kuljettu matka. Esimerkiksi, jos esine liikkuu suorassa linjassa ja kattaa 5 metrin etäisyyden, sen etäisyys ja siirtymä ovat samat.

5. Gravitaatiovoiman suuruus

Se viittaa voimaan, joka vetää puoleensa mitä tahansa kahta kappaletta massalla. Se on houkutteleva voima, koska sillä on taipumus vetää massoja yhteen. Voimme sanoa, että vetovoima on olemassa tai jokainen esine vetää puoleensa tai vetää kaikkia muita kohteita tässä universumissa. Se tunnetaan myös nimellä Newtonin universaali gravitaatiolaki. Tämän gravitaatiovoiman suuruus kahden kappaleen välillä, joiden massa on m1 ja m2, on esitetty matemaattisesti alla esitetyllä tavalla;

F = G x m1 x m2/r²

java lajittelumerkkijonoja

Kuinka laskea fyysisen suuren suuruus?

Jokaisella fyysisellä suurella on suuruus, joten se on mitattavissa. Mutta kaikkia fyysisiä suureita ei voida mitata samalla tavalla. Tämä johtuu siitä, että fyysinen suure voi olla kahta tyyppiä: skalaari ja vektori. Molemmat tyypit noudattavat erilaisia ​​algebran sääntöjä.

Skalaarimäärä:

Se on fysikaalinen suure, joka määritellään vain suuruudella tai sillä on vain suuruus, kuten massa, tilavuus, tiheys jne. Joten skalaarisuureen määrittämiseen tarvitaan vain suuruus ja yksikkö, suuntaa ei tarvita. Esimerkiksi 60 kg paino, jossa 60 on suuruus ja Kg on yksikkö. Skalaarisuureen suuruuden laskemiseksi on noudatettava lineaarista algebrasääntöä.

Samoin nopeus on myös skalaarisuure, koska sitä kuvaa vain sen suuruus. Se kertoo vain nopeuden, jolla esine liikkuu, ei kerro mitään suunnasta, johon se liikkuu. Joten objekti, joka liikkuu nopeammin, kattaa enemmän etäisyyttä kuin kohde, joka liikkuu hitaammin samassa ajassa.

Kuinka laskea skalaarisuureen suuruus:

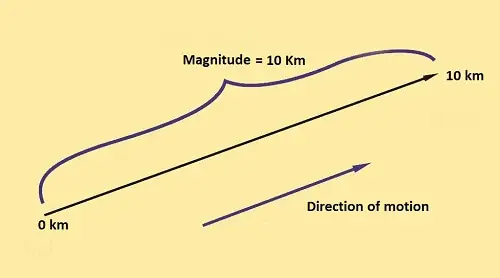
Sen laskenta on hyvin yksinkertainen. Jokapäiväisessä elämässämme laskemme skalaarisuureen monta kertaa. Esimerkiksi, kun kuljet 10 km:n matkan päästäksesi toimistoosi, tässä tapauksessa 10 km:n matka on skalaarisuure ja sen suuruus on 10 km, mikä vastaa kokonaismatkaa.

Toisessa esimerkissä oletetaan, että 100 ml vettä sekoitetaan 1 litraan puhdasta maitoa ja maidon kokonaismääräksi tai suuruudeksi tulee 1250 ml. Tässä suuruus lasketaan yksinkertaisella summauksella.

reagoi-taulukko

Vektorisuure

Se on fysikaalinen suure, jolla on sekä suuruus että suunta, kuten nopeus, siirtymä, voima jne. voimme sanoa, että se tarvitsee sekä suuruuden että suunnan täydelliseen kuvaukseensa. Joten vektorin määrittämiseen tarvitaan sekä suuruus että suunta. Esimerkiksi nopeus 60 km/h, pohjoiseen. Täällä esine liikkuu nopeudella 60 km/h (magnitudi) kohti pohjoista.

Kahden vektorisuureen yhteenlaskua ei voi tehdä tavallisella algebralla. Vektorisuure on merkitty nuolella kirjaimen tai jakson päällä, jonka toisessa päässä on nuoli, jossa nuoli kertoo suunnan.

analoginen viestintä

Kuinka laskea vektorisuureen suuruus:

Vektorisuureiden tapauksessa kahta tai useampaa vektoria voidaan kutsua yhtäläisiksi, jos niillä on sama suunta ja suuruus. Kun kerromme vektorisuureen positiivisella kokonaisluvulla, sen suuruus muuttuu, mutta suunta pysyy samana. Kuitenkin, kun kerromme sen negatiivisella kokonaisluvulla, sekä suuruus että suunta muuttuvat suunnan käänteessä ja suuruus kerrotaan luvun itseisarvolla.

Suuruusluokka

Suuruusluokka on karkea arvio jonkin koosta tai suuruudesta, ja se esitetään kymmenen potenssina. Se on jonkin arvioitu koko mitattuna 10 potenssilla. Esimerkiksi Maan koko on suuruusluokkaa 1020 kg.

Jos arvo on suuruusluokkaa suurempi kuin toinen arvo, se tarkoittaa, että se on kymmenen kertaa suurempi kuin toinen arvo. Samoin, kun se on kaksi suuruusluokkaa suurempi, se olisi sata kertaa suurempi. Suuruusluokka voidaan nähdä tieteellisissä merkinnöissä, joissa luku nostetaan potenssiin 10.

Kuinka löytää suuruusluokka?

Suuruusluokka 255 000 olisi 5, kun tämä arvo muunnetaan tieteelliseksi merkinnöiksi, 2,55 x 10⁵, 10 nostetaan 5:ksi^thkymmenen tehoa. Sen avulla voimme verrata eri lukujen suuruusluokkaa. Esimerkiksi,

A = 5,4 x 10⁶

B = 5,4 x 10⁸

Se osoittaa, että B on kaksi suuruusluokkaa suurempi kuin A.