Newtonin jäähdytyslaki on peruslaki, joka kuvaa kehon lämmönsiirtonopeutta ympäristöönsä säteilyn kautta. Tämä laki sanoo, että nopeus, jolla keho säteilee lämpöä, on suoraan verrannollinen kehon ja sen ympäristön lämpötilaeroon, koska lämpötilaero on pieni. eli mitä suurempi ero kehon ja sen ympäristön lämpötilan välillä on, sitä enemmän lämpöä häviää ja mitä alhaisempi lämpötila, sitä vähemmän lämpöä häviää. Newtonin jäähtymislaki on Stefan-Boltzmannin lain erikoistapaus.

Tässä artikkelissa opimme yksityiskohtaisesti Newtonin jäähdytyslaista, Newtonin jäähdytyslakia, sen johtamista, esimerkkejä ja muita yksityiskohtaisesti.

Newtonin jäähdytyslain määritelmä

Newton oli ensimmäinen, joka tutki kehon ympäristöön menettävän lämmön välistä suhdetta. Hän toteaa, että mitä suurempi lämpötilaero kohteen ja sen ympäristön välillä, sitä enemmän lämpöä keho säteilee.

Newtonin jäähtymislaki toteaa, että

Kehon lämpöhäviön nopeus on suoraan verrannollinen kehon ja sen ympäristön lämpötilaeroon, koska lämpötilaero ei ole suuri.

Tätä lakia käytetään selittämään, miksi kuuma vesi tai pöydälle jätetty maito jäähtyy nopeammin kuin pieni lämmin maito tai pöydälle jätetty vesi. Newtonin jäähtymislaki auttaa meitä mittaamaan kenen tahansa lämpötilaa varsinaisesti mittaamatta sitä, kun otetaan huomioon kehon alkulämpötila ja ympäristön lämpötila.

Newtonin jäähdytyskaavan laki

Newtonin jäähdytyslain kaava on kaava materiaalin lämpötilan laskemiseksi, kun se menettää lämpöä ympäristöönsä säteilyn kautta.

Newtonin jäähtymislain mukaan

Lämmönhäviön nopeus ( – dQ/dt) kehon lämpötila on suoraan verrannollinen lämpötilaeroon [ΔT = (T ₂ – T ₁ )] kehosta ja ympäristöstä.

mikroliittinen ydin

Voimme edustaa sitä mm.

– dQ/dt ∝ (T ₂ – T ₁ )

– dQ/dt = k(T ₂ – T ₁ )

missä,
k on suhteellisuusvakio

Ratkaisemalla yllä olevan differentiaaliyhtälön saamme,

T(t) = T _s + (T _O – T _s ) Se on ^-kt

missä,
t on aika
T(t) on kehon lämpötila hetkellä t
T _s on ympäristön lämpötila
T _O on kehon alkulämpötila
k on suhteellisuusvakio

Newtonin jäähtymislain johdanto

Newtonin jäähdytyslain kaava voidaan johtaa differentiaaliyhtälön ratkaisulla. Olkoon kappale, jonka massa on m ja jonka ominaislämpökapasiteetti on s, lämpötilassa T₂ja T₁on ympäristön lämpötila.

Jos lämpötila laskee vähän dT ₂ ajallaan dt , silloin hävinneen lämmön määrä on

dQ = ms dT ₂

Lämmönhäviön nopeus saadaan seuraavasti:

dQ/dt = ms (dT ₂ /dt)

Newtonin jäähtymislain mukaan

– dQ/dt = k(T ₂ – T ₁ )

Vertaamalla yllä olevaa yhtälöä

– ms (dT ₂ /dt) = k (T ₂ – T ₁ )

dT ₂ /(T ₂ –T ₁ ) = – (k / ms) dt

dT ₂ /(T ₂ – T ₁ ) = – Kdt

missä, K = k/m s

Yllä olevan yhtälön integrointi

Hirsi _{se on} (T ₂ – T ₁ ) = – K t + c

T ₂ = T ₁ + C’ ja ^{– Kt}

missä, C' = e ^c

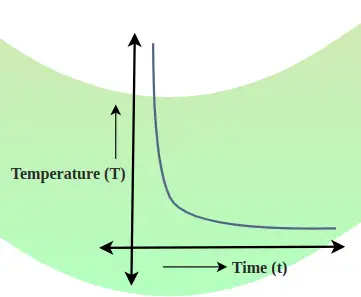
Kehon lämpötilan laskun ja ajan välinen suhde esitetään jäähtymiskäyrän avulla. Tämän kaavion kaltevuus näyttää lämpötilan laskunopeuden.

Jäähtymiskäyrä on kaavio, joka näyttää kehon lämpötilan ja ajan välisen suhteen. Lämpötilan laskun nopeus määräytyy käyrän tangentin kaltevuuden mukaan missä tahansa pisteessä. Alla lisätty kuva näyttää lämpötilan laskun ja ajan suhteen.

Yleisesti,

T(t) = T _A +(T _H -T _A )Se on ^-kt

missä
T(t) on lämpötila ajanhetkellä t
T _A on ympäristön lämpötila tai lämpötila
T _H on kuuman kohteen lämpötila
k on positiivinen vakio ja t on aika

Menetelmät Newtonin jäähdytyslain soveltamiseksi

Vakiojäähdytysnopeudella jäähtymisnopeus on suhteessa kehon keskilämpötilaan ajanjakson aikana, jolloin voimme laskea likimääräisen arvon käyttämällä Newtonin jäähtymislakia

dθ/dt = k(q – q _s )

missä,
q on kehon lämpötila
q _s on ympäristön lämpötila

Jos nyt kehon keskilämpötila on q, missä

q = (q _i + q _f )/2

Newtonin jäähdytyslain varmistus

Voimme helposti varmistaa Newtonin jäähdytyslain alla kuvatulla kokeella:

Kokeessa otamme kaksiseinäisen astian (V), jonka seinämien välissä on vettä. Kaksiseinäisen astian sisään otamme kuparikalorimetrin (C), joka sisältää kuumaa vettä.

Käytämme kahta lämpömittaria T₂mittaamaan veden lämpötilat kalorimetrissä ja T₁lämpötilan mittaamiseen kuumasta vedestä kaksoiseinien välissä. Saman aikavälin jälkeen molemmat lämpötilat merkitään muistiin ja kaavio login väliin_{se on}(T₂–T₁) ja aika (t) piirretään, joka näkyy suorana, jonka kaltevuus on negatiivinen.

java 8 ominaisuudet

Newtonin jäähdytyslain graafi

Newtonin jäähtymislain kaavio on lisätty alle, tässä kaaviossa näkyy kahden lämpötilan ja ajan välisen eron logaritmi.

Newtonin jäähdytyslain rajoitukset

Newtonin jäähdytyslain rajoituksia ovat mm.

• Newtonin jäähtymislaki pätee, jos kehon ja ympäristön lämpötilaero on pieni.
• Kehon lämpöhäviö on vain muodossa Säteily .
• Ympäristön lämpötilan tulee pysyä vakiona kehon jäähtymisen aikana, jos ei, niin Newtonin jäähtymislaki ei päde.

Newtonin jäähdytyslain sovellukset

Newtonin jäähtymislain sovelluksia ovat mm.

• Arvioida kuinka kauan lämmin esine kestää jäähtyä tiettyyn lämpötilaan.
• Jääkaapissa olevan juoman lämpötilan määrittäminen tietyn ajan kuluttua.
• Se auttaa ilmaisemaan kuolinajan tarkastelemalla mahdollista ruumiinlämpöä kuolinhetkellä ja senhetkistä ruumiinlämpöä.

Lue lisää,

• Ominaislämpökapasiteetti
• Termodynamiikan peruskäsite
• Termodynaamiset prosessit

Ratkaistut esimerkit Newtonin jäähtymislaki

Esimerkki 1: Kuumalla ruoalla täytetty pannu jäähtyy 94 °C:sta 86 °C:seen kahdessa minuutissa, kun huoneen lämpötila on 20 °C. Kuinka kauan kestää jäähtyä 71 °C:sta 69 °C:seen?

Ratkaisu:

94 °C ja 86 °C keskilämpötila on 90 °C,

• T₂= 90 °C
• T₁= 20 °C

Pudota tem. ruoan lämpötila on 8 °C kahdessa minuutissa.

Newtonin jäähtymislain mukaan

– dQ/dt = k(T ₂ –T ₁ )

java-merkki merkkijonoon

8 °C /2 min = k(90–20)

4 = k(70) ……… (1)

Keskilämpötila 69 °C ja 71 °C on 70 °C

• T₂= 70 °C
• T₁= 20 °C

Newtonin jäähtymislain mukaan

2 °C /dt = k(70–20) ……(2)

Yhtälöistä (1) ja (2),

Ajan muutos = 0,7 min = = 42 sekuntia

Näin ollen ruoan jäähtyminen 71 °C:sta 69 °C:seen kestää 42 sekuntia.

Esimerkki 2: Kehoa, jonka lämpötila on 40 ºC, pidetään ympäristössä, jonka lämpötila on 20 ºC. On havaittu, että sen lämpötila laskee 35 ºC:een 10 minuutissa. Selvitä, kuinka paljon enemmän aikaa kestää, että keho saavuttaa 30 ºC:n lämpötilan.

Ratkaisu:

Annettu,

• q_i= (40 - 20) ºC
• q_f= (35 - 20) ºC

Newtonin jäähdytyslain mukaan

q _f = q _i se on ^-kt

Nyt aikavälille, jolloin lämpötila laskee 40 ºC:sta 35 ºC:seen.

(35 – 20) = (40 – 20) ja^(10k)

se on^-10k= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

Nyt käytän taas Newonin kaavaa,

(30 – 20) = (35 – 20)e^-kt

c# mallikoodi

10 = 15e^-kt

se on^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

Käyttämällä k:n arvoa,

t = 0,40546/0,02876

t = 14,098 min

Eli aika, jonka keho saavuttaa 30 ºC:n lämpötilan, on 14,098 minuuttia

Esimerkki 3: Öljy kuumennetaan 70 ºC:seen. Se jäähtyy 50 ºC:seen 6 minuutin kuluttua. Laske aika, jonka öljy jäähtyy 50 ºC:sta 40 ºC:een, kun otetaan huomioon ympäristön lämpötila T _s = 25 ºC

Ratkaisu:

Annettu,

Öljyn lämpötila 6 minuutin kuluttua eli T(t) on 50 ºC

• Ympäristön lämpötila T_s= 25 ºC
• Öljyn lämpötila, T_O= 70 ºC
• Aika jäähtyä 50 ºC:een = 6 min

Newtonin jäähtymislain mukaan

T(t) = T_s+ (T₀– T_s) Se on^-kt

{T(t) – T_s}/(T_O– T_s) = ja^-kt

-kt = ln[(T(t) – T_s)/(T_O– T_s)] ………(1)

Korvaa arvot

-kt = ln[(50-25)/(70-25)]

-k = (ln 0,55556)/6

k = 0,09796

Keskimääräinen lämpötila 50 ºC - 40 ºC on yhtä suuri kuin 45 ºC

java kokonaisluku

Jälleen käyttämällä Newtonin jäähdytyslakia

-(0,09796)t = ln[(45-25)/(70-25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8,278 min

Siten öljyn jäähtymiseen kuluva aika 50 ºC:sta 40 ºC:seen on 8,278 min

Esimerkki 4: Vesi kuumennetaan 80 ºC:seen 10 minuutiksi. Kuinka paljon sen lämpötila olisi celsiusasteina, jos k = 0,056 minuutissa ja ympäristön lämpötila on 25 ºC?

Ratkaisu:

Annettu,

• Ympäristön lämpötila T_s= 25 ºC
• Veden lämpötila T₀= 80 ºC
• Aika, jonka vettä kuumennetaan (t) = 10 min
• Vakion k arvo = 0,056.

Newtonin jäähtymislain mukaan

T(t) = T_s+ (T₀– T_s) Se on^-kt

Arvon korvaaminen

T(t) = 25 + (80 - 25)e^{(0,056 × 10)}

T(t) = 25 + 55 e^{(0,056 × 10)}

T(t) = 25 + 31,42

T(t) = 56,42

10 minuutin kuluttua veden lämpötila olisi 56,42 ºC.

Usein kysytyt kysymykset Newtonin jäähdytyslaista

K1: Mikä on Newtonin jäähdytyslaki?

Vastaus:

Newtonin jäähtymislaki sanoo, että kehon lämmönhukan nopeus on suoraan verrannollinen kehon ja sen ympäristön lämpötilaeroon.

Q2: Mikä on Newtonin jäähdytyskaavan laki?

Vastaus:

Newtonin jäähdytyslain kaava sanoo, että

T(t) = T _s + (T _O – T _s ) Se on ^-kt

Q3: Mikä on k Newtonin jäähdytyslaissa?

Vastaus:

The k Newtonin jäähdytyslain kaava on vakio, joka riippuu materiaalista, eli materiaalin muuttaminen muuttaa k Newtonin jäähtymislaissa.

K4: Miksi Hot Milk on helpompi juoda kulhosta kuin lasista?

Vastaus:

Kulhon pinta-ala on suurempi kuin lasilla, joten enemmän lämpöä häviää ympäristöönsä kulhon läpi lämpösäteilynä ja siten meidän on helpompi juoda kuumaa maitoa kulhosta.