Tietojenkäsittelytieteessä on joitakin ongelmia, joihin ei ole vielä löydetty ratkaisua, tehtävät on jaettu luokkiin, jotka tunnetaan nimellä Monimutkaisuusluokat . Monimutkaisuusteoriassa monimutkaisuusluokka on joukko ongelmia, joihin liittyy monimutkaisuus. Nämä luokat auttavat tutkijoita ryhmittelemään ongelmia sen mukaan, kuinka paljon aikaa ja tilaa he tarvitsevat ongelmien ratkaisemiseen ja ratkaisujen tarkistamiseen. Se on laskentateorian haara, joka käsittelee ongelman ratkaisemiseen tarvittavia resursseja.
matriisi, joka lisää elementtejä java
Yleisiä resursseja ovat aika ja tila, eli kuinka paljon aikaa algoritmilla kuluu ongelman ratkaisemiseen ja vastaavaa muistin käyttöä.
- Algoritmin aikamonimutkaisuutta käytetään kuvaamaan ongelman ratkaisemiseen tarvittavien vaiheiden määrää, mutta sitä voidaan käyttää myös kuvaamaan, kuinka kauan vastauksen tarkistaminen kestää.
- Algoritmin tilan monimutkaisuus kuvaa kuinka paljon muistia tarvitaan algoritmin toimintaan.
Monimutkaisuustunnit ovat hyödyllisiä samantyyppisten ongelmien järjestämisessä.
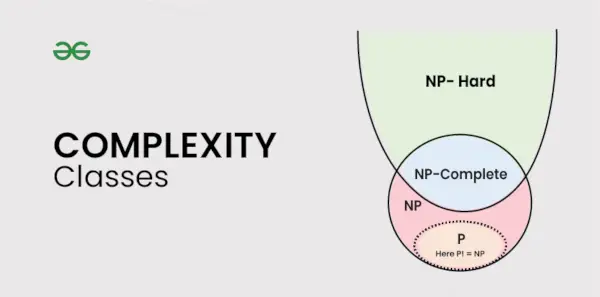
Monimutkaisuusluokkien tyypit
Tässä artikkelissa käsitellään seuraavia monimutkaisuusluokkia:
- P-luokka
- NP luokka
- CoNP-luokka
- NP-kovaa
- NP-täydellinen
P-luokka
P-luokassa P tarkoittaa Polynomiaika. Se on joukko päätösongelmia (ongelmia, joihin on vastaus kyllä tai ei), jotka voidaan ratkaista deterministisellä koneella polynomiajassa.
Ominaisuudet:
- Ratkaisu siihen P ongelma s on helppo löytää.
- P on usein luokka laskennallisia ongelmia, jotka ovat ratkaistavissa ja seurattavissa. Tractable tarkoittaa, että ongelmat voidaan ratkaista sekä teoriassa että käytännössä. Mutta ongelmat, jotka voidaan ratkaista teoriassa mutta eivät käytännössä, tunnetaan ratkaisemattomina.
Tämä luokka sisältää monia ongelmia:
- Suurimman yhteisen jakajan laskeminen.
- Maksimivastineen löytäminen.
- Yhdistä lajittelu
NP luokka
NP NP-luokassa tarkoittaa Ei-deterministinen polynomiaika . Se on joukko päätösongelmia, jotka voidaan ratkaista ei-deterministisellä koneella polynomiajassa.
Ominaisuudet:
- NP-luokan ratkaisuja on vaikea löytää, koska ne ratkaistaan epädeterministisellä koneella, mutta ratkaisut on helppo todentaa.
- NP:n tehtävät voidaan varmistaa Turingin koneella polynomiajassa.
Esimerkki:
java yhteys mysql
Tarkastellaanpa esimerkkiä ymmärtääksemme paremmin NP luokka . Oletetaan, että yrityksellä on yhteensä 1000 työntekijöillä on ainutlaatuinen työntekijä tunnukset . Oletetaan, että niitä on 200 huoneita heille. Valikoima 200 työntekijät on yhdistettävä pariksi, mutta yhtiön toimitusjohtajalla on tiedot niistä työntekijöistä, jotka eivät henkilökohtaisista syistä voi työskennellä samassa huoneessa.
Tämä on esimerkki an ESIM ongelma. Koska on helppo tarkistaa, onko annettu valinta 200 työtoverin ehdottamat työntekijät ovat tyydyttäviä tai ei, eli toimitusjohtajan antamassa listassa ei näy työtovereiden luettelosta otettua paria. Mutta sellaisen luettelon luominen tyhjästä näyttää olevan niin vaikeaa, että se on täysin epäkäytännöllistä.
Se osoittaa, että jos joku voi tarjota meille ratkaisun ongelmaan, voimme löytää oikean ja väärän parin polynomiajassa. Näin ollen ESIM luokkaongelma, vastaus on mahdollinen, joka voidaan laskea polynomiajassa.
Tämä luokka sisältää monia ongelmia, jotka halutaan ratkaista tehokkaasti:
- Boolean Satisfiability Problem (SAT).
- Hamiltonin polun ongelma.
- Graafinen väritys.
Co-NP-luokka
Co-NP tarkoittaa NP-luokan komplementtia. Se tarkoittaa, että jos vastaus ongelmaan Co-NP:ssä on Ei, on olemassa todiste, joka voidaan tarkistaa polynomiajassa.
Ominaisuudet:
css läpinäkyvyyden siirtyminen
- Jos ongelma X on NP:ssä, niin sen komplementti X' on myös CoNP:ssä.
- NP- ja CoNP-tehtävässä ei tarvitse varmentaa kaikkia vastauksia kerralla polynomiajassa, vaan on tarpeen varmistaa vain yksi tietty vastaus kyllä tai ei polynomiajassa, jotta ongelma olisi NP:ssä tai CoNP:ssä.
Joitakin esimerkkejä CoNP-ongelmista ovat:
- Alkuluvun tarkistaminen.
- Kokonaislukufaktorointi.
NP-kova luokka
NP-kova ongelma on vähintään yhtä vaikea kuin vaikein ongelma NP:ssä, ja se on sellainen ongelmaluokka, että jokainen NP:n ongelma pelkistyy NP-kovaksi.
Ominaisuudet:
- Kaikki NP-kovat ongelmat eivät ole NP:ssä.
- Niiden tarkistaminen kestää kauan. Tämä tarkoittaa, että jos NP-kovaan ongelmaan annetaan ratkaisu, kestää kauan tarkistaa, onko se oikea vai ei.
- Tehtävä A on NP-kovassa, jos jokaiselle NP:n tehtävälle L on olemassa polynomiaikainen pelkistys L:stä A:han.
Joitakin esimerkkejä Np-hardin ongelmista ovat:
- Pysäytysongelma.
- Hyväksytyt Boolen kaavat.
- Ei Hamiltonin sykliä.
NP-täydellinen luokka
Ongelma on NP-täydellinen, jos se on sekä NP että NP-kova. NP-täydelliset ongelmat ovat vaikeita ongelmia NP:ssä.
Ominaisuudet:
- NP-täydet tehtävät ovat erityisiä, koska mikä tahansa NP-luokan ongelma voidaan muuntaa tai pelkistää NP-täydellisiksi ongelmiksi polynomiajassa.
- Jos NP-täydellinen tehtävä voitaisiin ratkaista polynomiajassa, niin mikä tahansa NP-tehtävä voitaisiin ratkaista myös polynomiajassa.
Joitakin esimerkkiongelmia ovat:
- Hamiltonin sykli.
- Tyytyväisyys.
- Vertex kansi .
| Monimutkaisuusluokka | Ominaisuus |
| P | Helposti ratkaistavissa polynomiajassa. |
| ESIM | Kyllä, vastaukset voidaan tarkistaa polynomiajassa. |
| Co-NP | Ei, vastaukset voidaan tarkistaa polynomiajassa. |
| NP-kovaa | Kaikki NP-kovat ongelmat eivät ole NP:ssä ja niiden tarkistaminen kestää kauan. |
| NP-täydellinen | Ongelma, joka on NP ja NP-kova, on NP-täydellinen. |
